代码训练营第二十天|530.二叉搜索树的最小绝对差 ● 501.二叉搜索树中的众数 ● 236. 二叉树的最近公共祖先

news2024/9/21 0:33:47

530 .二叉搜索树的最小绝对差

看完题后的思路

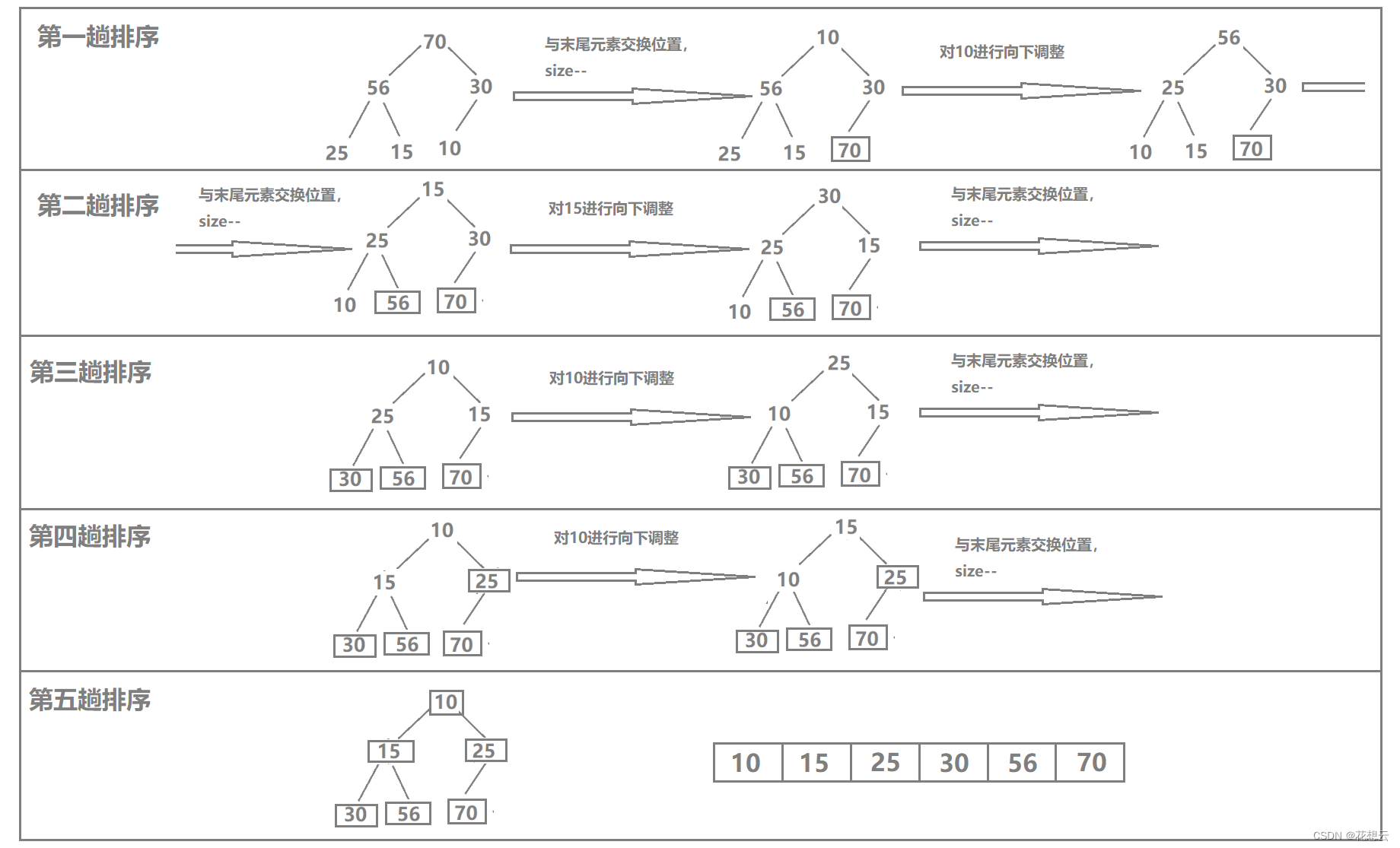
因为是二叉搜索树，所以直接按照二叉搜索树中序遍历，得到递增序列。遍历过程中一个指针指向遍历过的前一个元素
pre=null；

void f（root）
if root==null return
递归
f（left）
计算差值
pre=root
f（root）
pre可以作为一个全局变量，在操作完元素后赋下一个值

代码

  TreeNode pre;
    int resgetMinimumDifference=Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        getMinimumDifferenceDG(root);
        return resgetMinimumDifference;
    }
    public void getMinimumDifferenceDG(TreeNode root) {
        if (root==null){
            return;
        }
        getMinimumDifferenceDG(root.left);
        if (pre!=null){
            resgetMinimumDifference=Math.min(Math.abs(root.val-pre.val),resgetMinimumDifference);
        }
        pre=root;
        getMinimumDifferenceDG(root.right);
    }

复杂度

在这里插入图片描述
迭代算法略

收获

本题解决了二叉树中的双指针的写法

530.二叉搜索树的最小绝对差

看完题后的思路

使用中序遍历，if 当前元素！=pre || pre==null ，进行新一轮的计数，上一元素是否是众数，否则次数值加一
res【】

void f（root）
if （root==null） return
中序+pre

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
 ArrayList<Integer> findModeRes = new ArrayList<Integer>();
    int count=0;
    int maxCount=-1;
  TreeNode pre;
    public int[] findMode(TreeNode root) {
     
        findModeDG(root);
        int[] res = new int[findModeRes.size()];
        int i=0;
        for (Integer integer : findModeRes) {
            res[i++]=integer;
        }
        return res;
    }
   public void findModeDG(TreeNode root) {
        if (root==null){
            return;
        }
        findModeDG(root.left);
        // 没有考虑单节点情况
        if (pre==null||pre.val!=root.val){
            count=1;
        }else{
            count++;
        }
        pre=root;
       
            if (count>maxCount){
                findModeRes.clear();// 清空 加新的众数
                findModeRes.add(root.val);
                maxCount=count;
               
            }else if (count==maxCount){
                findModeRes.add(root.val);
              
            }
        findModeDG(root.right);
    }
}

复杂度

本题使用一遍迭代就求出了众数，具体做法为

统计元素个数
根据元素个数做相应操作

在这里插入图片描述

收获

1. 三刷写一遍
2. 求数组众数的最优写法

二叉树的最近公共祖先

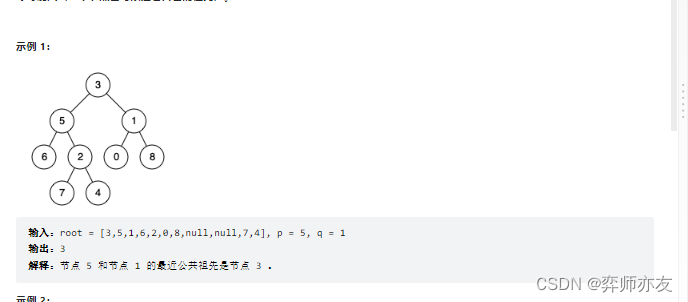
看完题后的思路

从下往上走，使用后续遍历

node f（root）
递归终止条件
if root==null
return null；
递归逻辑
if（root.val=其中一个）{
return root；
}
left=f（左）
right=f（右）
if（左右全为空）{
return null}
if （左右只有一个为空）{
return 不为空的那个；
}
return 左右的公共节点，就是我

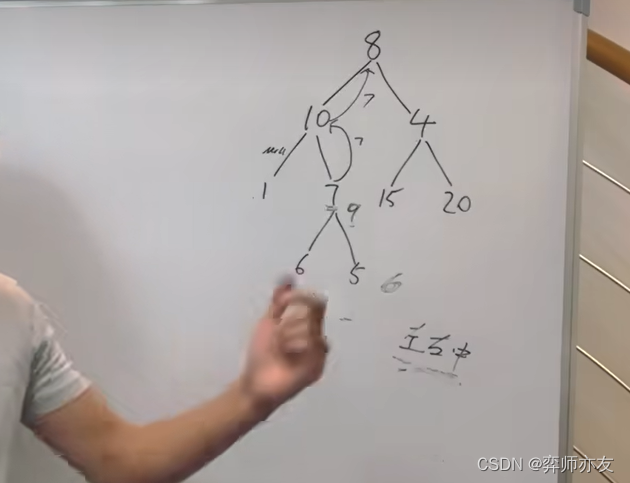
思路

本题既有从上到下，又有从下到上。前序负责从上到下，后续负责从下到上前序是，分别判断每一个节点是不是与目标节点相同，如果相同，终止递归
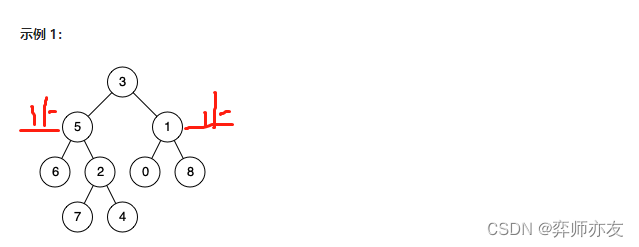
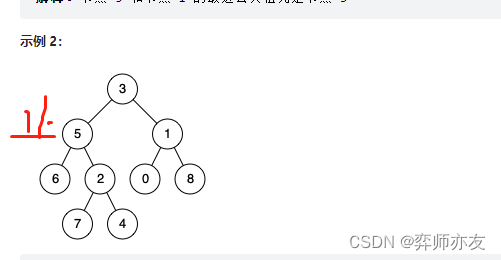
在这里插入图片描述

后续时，判断从下到上的返回值，如果两个返回值，则说明我是公共节点，一个返回值，该返回值是公共节点，如果没有返回值，则公共节点为空。

代码

        }
   //236. 二叉树的最近公共祖先
   public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root==null){
            return null;
        }
        // 先前序
        if (root==p||root==q){
            return root;
        }
       TreeNode left = lowestCommonAncestor(root.left, p, q);
       TreeNode right = lowestCommonAncestor(root.right, p, q);
       if (left==null&&right==null){
           return null;
       }
       // 有一个空
       if (left==null||right==null){
           return left!=null ? left : right;
       }
       //如果左右都不为空，返回自己
       return root;

   }