本节介绍电机的基本物理量和基本关系
本节介绍直流电机的静态特性以及动态特性
本节介绍直流电机的控制方法、启动方法、稳定运行条件
本节介绍直流电动机的四种工作状态
本节介绍控制系统中应用的直流电动机的类型
文章目录
- 基础知识
- 基本物理量:电磁转矩与电枢反电势
- 基本关系:转矩平衡和电压平衡
- 直流发电机
- 直流电动机的静态特性与控制方法
- 静态特性方程
- 电机的控制
- 电枢控制时的机械特性和调节特性
- 磁场控制时的机械特性和调节特性
- 改变电枢回路串电阻时的机械特性
- 稳态运行时的功率关系
- 他励式直流电机的工作特性
- 直流电机的启动
- 电机稳定运行的条件
- 负载的转矩特性
- 稳定运行的条件
- 调速方式与负载类型的配合
- 直流电动机的四种工作状态
- 1 电动机状态
- 2 发电机状态
- 3 能耗制动状态
- 4 反接制动状态
- 直流电机的动态特性
- 电枢控制时的动态特性
- 磁场控制时的动态特性
- 控制系统中应用的直流电动机
- 直流伺服电机
- 直流力矩电动机
- 有限转角直流力矩电动机
- 直流电机的选型原则
基础知识
这一部分分析的前提:
- 不考虑磁化曲线的非线性
- 不考虑电枢反应
- 忽略电枢上槽的影响
基本物理量:电磁转矩与电枢反电势
电磁转矩
定义:直流电机正常工作时,电枢绕组在磁场中受力形成的总转矩。
对于电动机:拖动转矩(驱动)
对于发电机:阻转矩(制动)
计算:

计算电磁转矩的两个公式:
T
e
m
=
C
t
Φ
I
a
T
e
m
=
K
t
I
a
T_{em}=C_t\Phi I_a\\ T_{em}=K_tI_a
Tem=CtΦIaTem=KtIa (
Φ
\Phi
Φ为定值)
C
t
C_t
Ct是电机的一个常数,
C
t
=
p
N
2
π
a
C_t=\frac{pN}{2\pi a}
Ct=2πapN
K
t
K_t
Kt称为转矩灵敏度,
K
t
=
C
t
Φ
K_t=C_t\Phi
Kt=CtΦ ,单位
N
⋅
m
/
A
N\cdot m/A
N⋅m/A
N为导体数,每一匝线圈的每一个有效边都是一个导体
可以看出:制造好的电机,其电磁转矩和气隙磁通以及电枢电流成正比。
「注意」
- 实际电磁转矩是波动的
因为电枢存在齿槽,槽内磁密小于槽外磁密,之前求的都是平均值 - 有齿槽时和假定无齿槽时产生的电磁转矩完全相等
- 有齿槽时,主要是铁心的齿受力
电枢反电势
定义:直流电机正常工作时,电枢绕组切割气隙磁通产生的一对电刷间的电动势
发电机:电源电势,与电枢电流同方向
电动机:反电势,与电枢电流反方向
计算:

计算电枢反电势的两个公式:
E
a
=
C
e
Φ
n
E_a=C_e\Phi n
Ea=CeΦn
E
a
=
K
e
ω
E_a=K_e\omega
Ea=Keω
C
e
C_e
Ce称为电势常数,
C
e
=
p
N
60
a
C_e=\frac{pN}{60a}
Ce=60apN
K
e
K_e
Ke称为电势系数,单位
V
/
(
r
a
d
/
s
)
V/(rad/s)
V/(rad/s),
K
e
=
C
e
Φ
⋅
60
2
π
K_e=C_e\Phi\cdot \frac{60}{2\pi}
Ke=CeΦ⋅2π60
可以看出,电枢反电势与电机结构、气隙磁通、转速有关。
「说明」
- 感应电势实际是波动的
因为实际电机有槽,而电枢导体集中在槽内,并不是均匀分布在电枢表面。 - 波动的频率为 f s = z n 60 f_s=\frac{zn}{60} fs=60zn ,z:齿数
- 波动的相对大小用波纹系数表示:
ε = U m a x − U m i n U m a x + U m i n \varepsilon=\displaystyle{\frac{U_{max}-U_{min}}{U_{max}+U_{min}}} ε=Umax+UminUmax−Umin
Ke和Kt
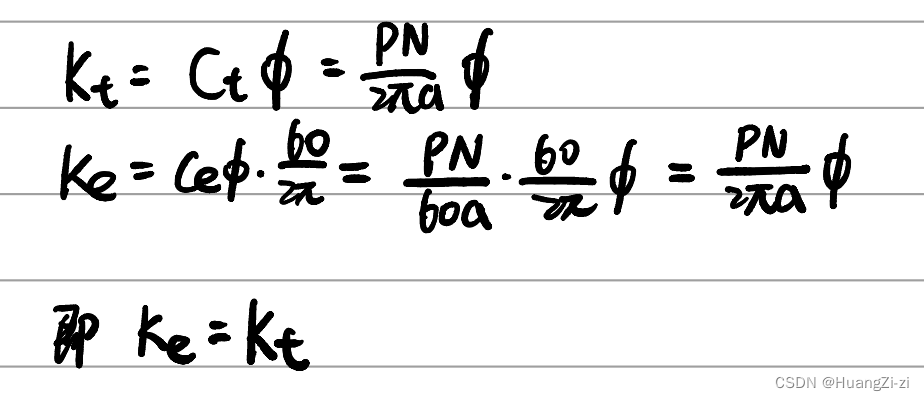
在采用国际标准单位制时,
K
e
=
K
t
K_e=K_t
Ke=Kt
在这里还可以推出:
C
t
=
60
2
π
C
e
≈
9.55
C
e
C_t=\frac{60}{2\pi}C_e\approx9.55C_e
Ct=2π60Ce≈9.55Ce
基本关系:转矩平衡和电压平衡
转矩平衡方程
电磁转矩之前介绍过了。
负载转矩也很好理解,就是电动机带动的负载带来的阻力转矩。
T0为阻转矩,包含了电动机各处的摩擦、铁心中涡流、磁滞损耗引起的阻力转矩。
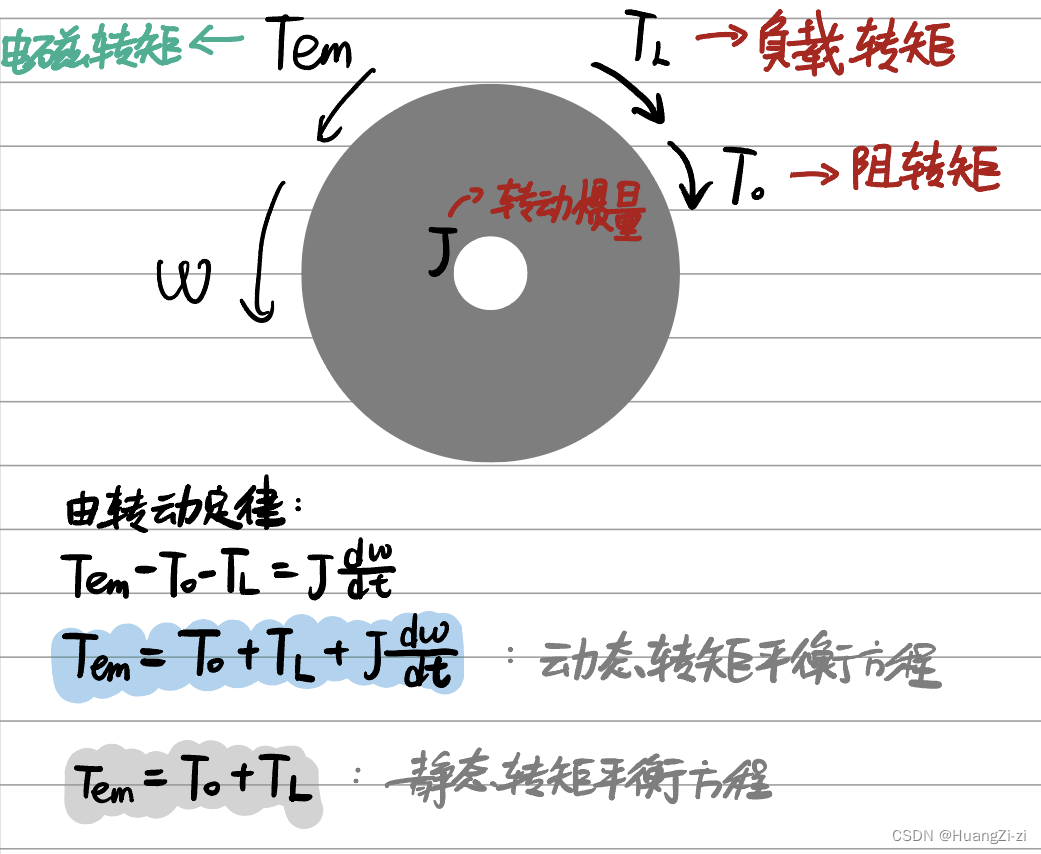
这个转矩平衡方程说白了就是刚体的定轴转动定理:
T
e
m
=
T
0
+
T
L
+
J
d
ω
d
t
T_{em}=\displaystyle{T_0+T_L+J\frac{d\omega}{dt}}
Tem=T0+TL+Jdtdω
定义输出转矩为T2:

电压平衡方程
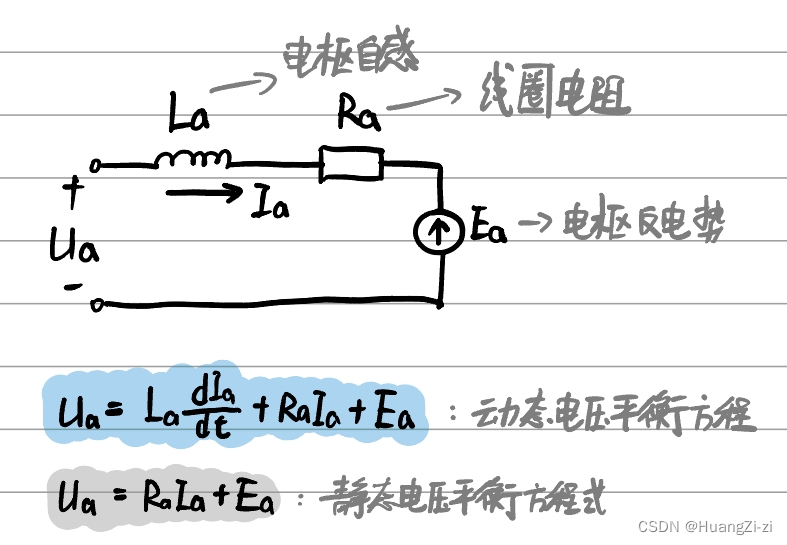
电压平衡方程说白了就是欧姆定律:
U
a
=
L
a
d
I
a
d
t
+
R
a
I
a
+
E
a
U_a=\displaystyle{L_a\frac{dI_a}{dt}+R_aI_a+E_a}
Ua=LadtdIa+RaIa+Ea
直流发电机
之前说过电动机具有可逆性。当直流电机被外力拖动而旋转时,电枢两端就会产生直流电压。
对于直流发电机,电磁转矩和电枢反电势与电动机完全相同。电压平衡方程仅仅将电枢电压和电枢反电势交换位置,转矩平衡方程仅仅将电磁转矩与输入\输出转矩交换位置。
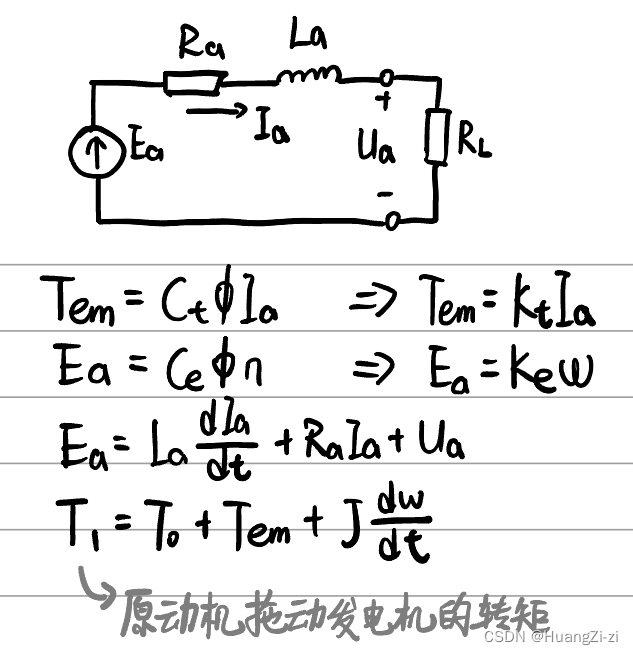
发电机的特点是,电流的实际方向与电枢电动势相同。
直流电动机的静态特性与控制方法
静态:直流电机的控制电压和负载转矩不变,电机的电流和转速为恒定值的状态
常用的静态特性有:
机械特性:一定输入下,静态时转速与转矩的关系
调节特性:一定电磁转矩下,转速与控制量之间的关系
静态特性方程

静态特性方程:
n
=
U
a
C
e
Φ
−
T
e
m
R
a
K
e
K
t
n=\displaystyle{\frac{U_a}{C_e\Phi}-\frac{T_{em}R_a}{K_eK_t}}
n=CeΦUa−KeKtTemRa
利用静态特性做个例题:

除了静态特性,电磁转矩、电枢反电势以及转矩平衡、电压平衡四个方程也很重要。
电机的控制
调速:改变和控制电机的转速。按照其平滑性可以分为无级调速和有级调速。
开环调速方法:改变电枢电压,改变气隙磁通,改变电枢回路电阻。
控制方法:
电枢控制:输入量为电枢电压
磁场控制:输入量是励磁电流,励磁电压,或者磁通
「闭环控制系统中,被控量可以是转速,也可以是转矩或转角。开环系统被控量是转速。」
电枢控制时的机械特性和调节特性
电枢控制时的机械特性
在静态特性方程中,固定Ua,画出转速n和电磁转矩Tem之间的关系:
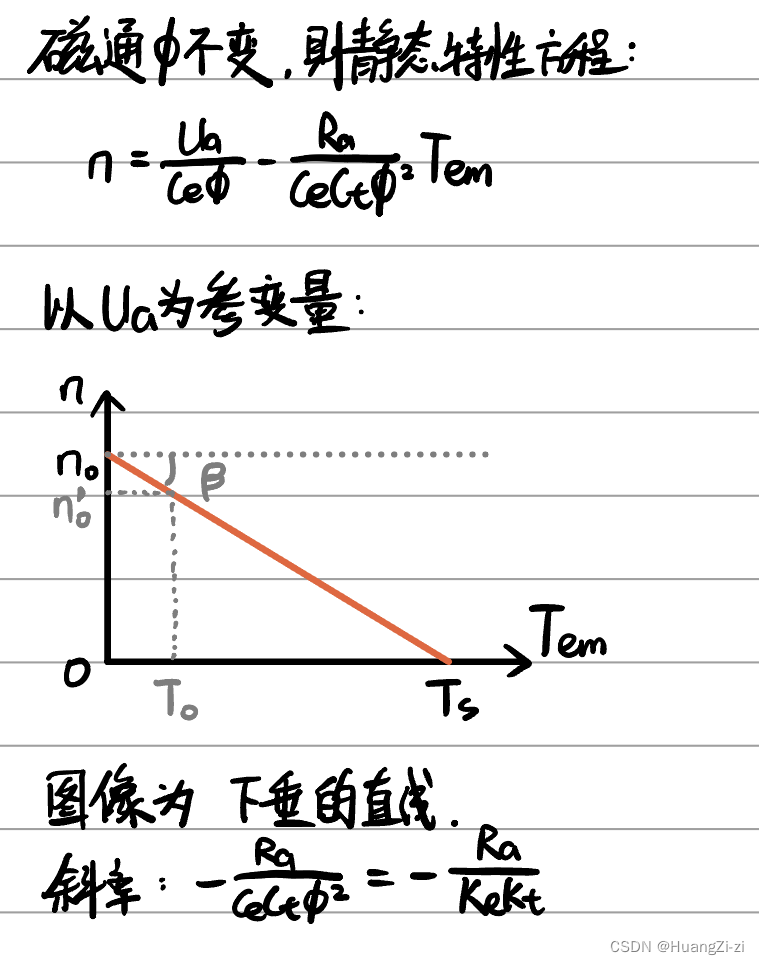
理想空载转速:
T
e
m
=
0
,
n
0
=
U
a
C
e
Φ
T_{em}=0,n_0=\frac{U_a}{C_e\Phi}
Tem=0,n0=CeΦUa
实际空载转速:
T
e
m
=
T
0
→
n
0
′
T_{em}=T_0\to n_0'
Tem=T0→n0′(有阻转矩)
堵转转矩:
n
=
0
,
T
s
=
U
a
R
a
C
t
Φ
=
I
s
C
t
Φ
=
I
s
K
t
n=0,T_s=\frac{U_a}{R_a}C_t\Phi=I_sC_t\Phi=I_sK_t
n=0,Ts=RaUaCtΦ=IsCtΦ=IsKt
称这里的Is为启动电流,因为不仅堵转时适用这个关系,启动时也适用这个关系。
机械特性硬度: β \beta β越小,机械特性越硬(转速改变量: Δ n = Δ T ⋅ tan β \Delta n=\Delta T\cdot\tan{\beta} Δn=ΔT⋅tanβ, β \beta β越小,转速越不容易因转矩改变而变化)
机械特性族:
Ua取值不同时画出的一族平行直线
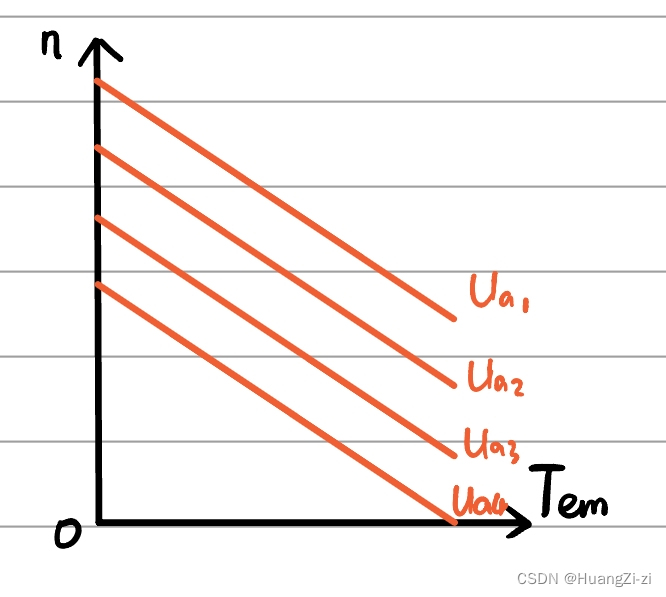
U
a
U_a
Ua越大,直线越高。
n
0
n_0
n0与
U
a
U_a
Ua呈线性关系。
斜率与
U
a
U_a
Ua无关。
通过这个例题看一下电枢电压是如何控制转速的:
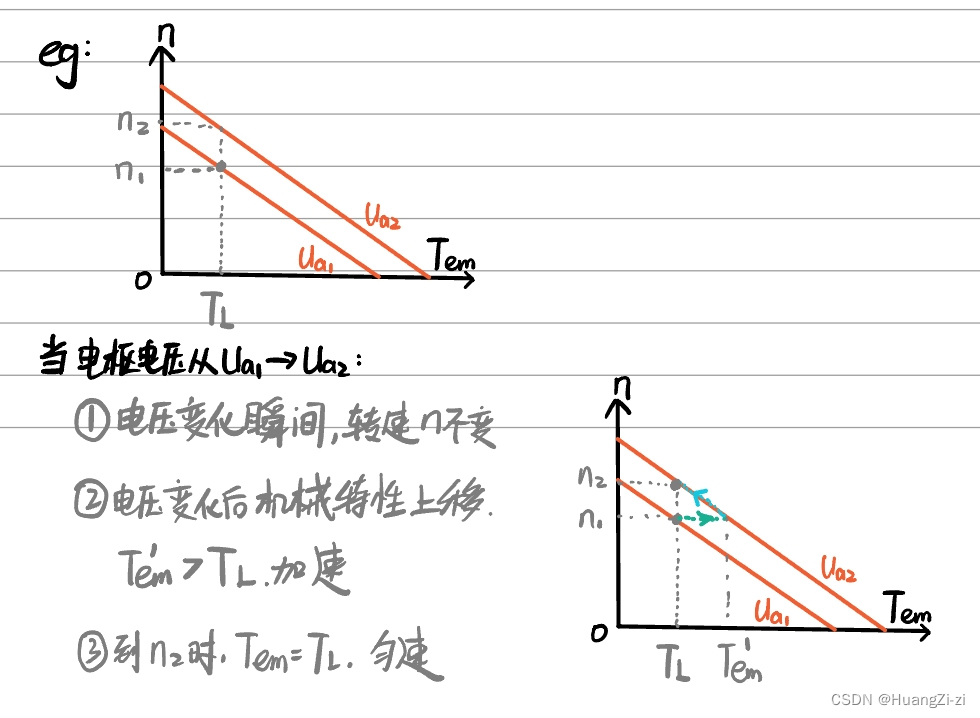
电枢控制时的调节特性
复习一下调节特性:电磁转矩为参变量时转速与电枢电压的关系。
在静态特性方程中,固定Tem,画出n和Ua之间的关系:
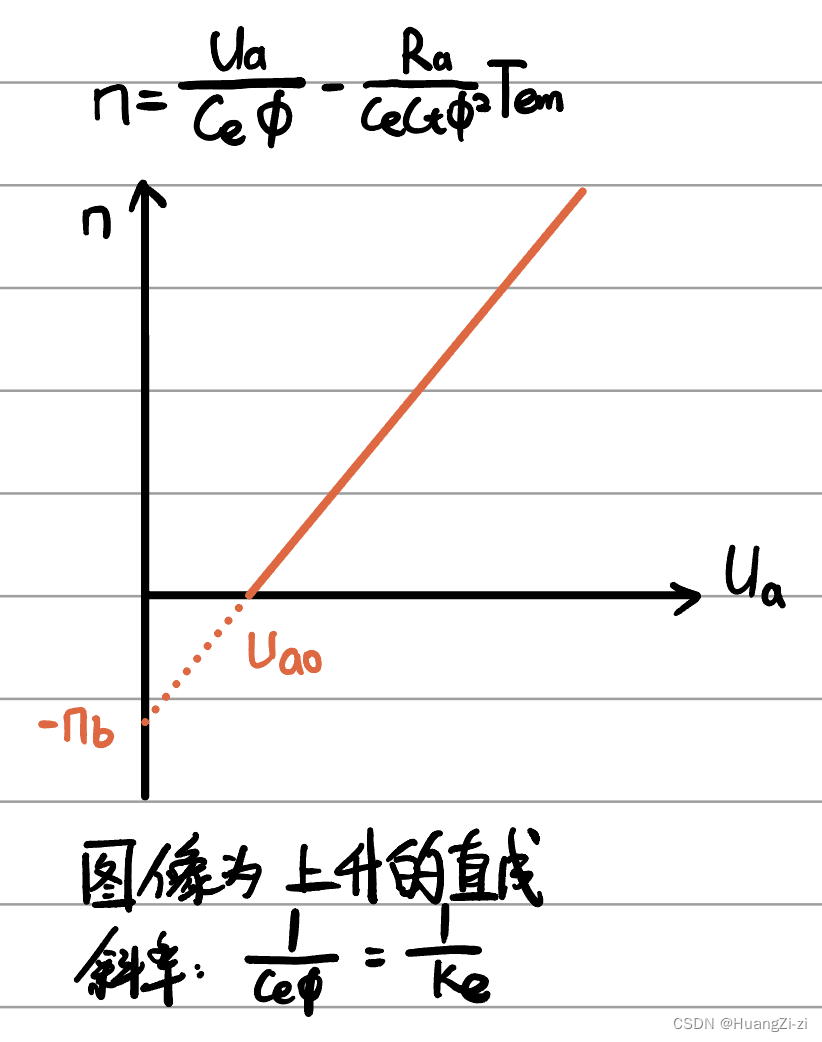
同样的,调节特性也是一族平行直线,称为调节特性族:
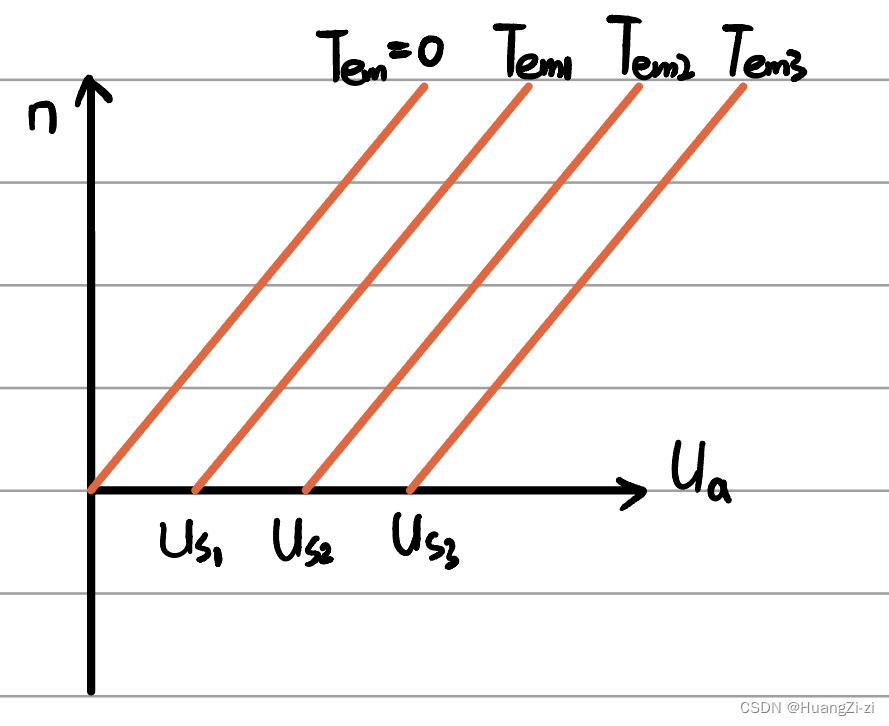
Tem越大,直线越靠右。其中Tem=0的直线过原点。
与横轴交点:
U
s
=
T
e
m
R
a
C
t
Φ
=
T
c
R
a
C
t
Φ
\displaystyle{U_s=\frac{T_{em}R_a}{C_t\Phi}=\frac{T_cR_a}{C_t\Phi}}
Us=CtΦTemRa=CtΦTcRa
T
c
T_c
Tc为总阻转矩
启动电压:Us。Tem=0的直线是理想情况,实际上由于摩擦力和负载,电枢电压需要达到一定值电机才能启动。启动电压也称死区电压。
启动电流:Is。 I s = U s R a I_s=\frac{U_s}{R_a} Is=RaUs
电枢控制的优缺点
优点:
- 机械特性和调节特性曲线族都是平行直线,是理想的线性元件,可以平滑调速
缺点:
- 以Ua为控制量,导致控制功率 U a I a U_aI_a UaIa较大。对于较大的电机,需要用大容量的功率放大器。
- 只能在基速以下调速(调速范围不能超过额定转速)
磁场控制时的机械特性和调节特性
磁场控制:改变励磁电压 U f U_f Uf和电流 I f I_f If
机械特性
固定磁通
Φ
\Phi
Φ,画出转速n和转矩
T
e
m
T_{em}
Tem的关系:
改变
Φ
\Phi
Φ的大小,可以画出机械特性族:
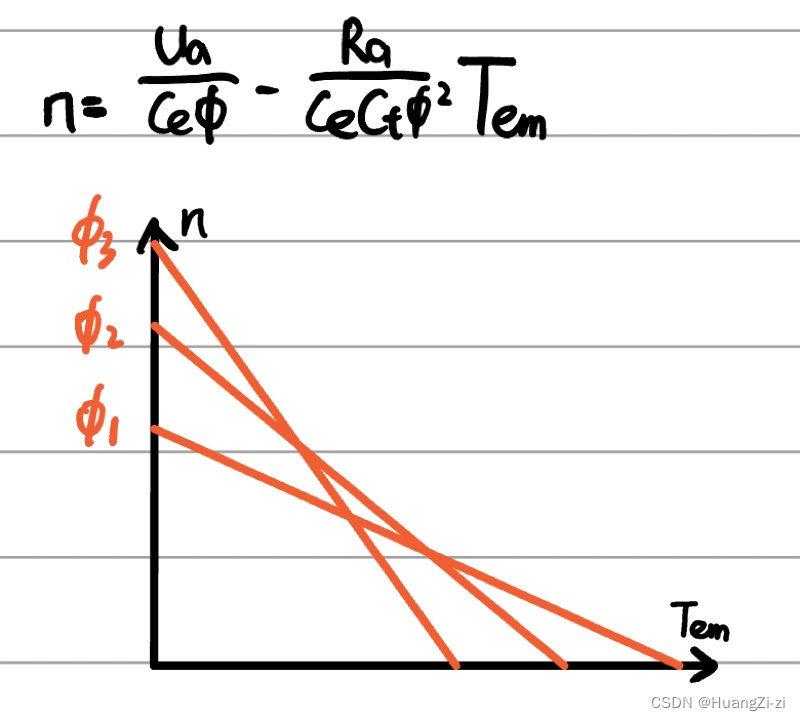
机械特性族是交叉的直线。 Φ \Phi Φ越大,直线越平缓。
调节特性
固定转矩
T
e
m
T_{em}
Tem,画出转速n与磁通
Φ
\Phi
Φ的关系:
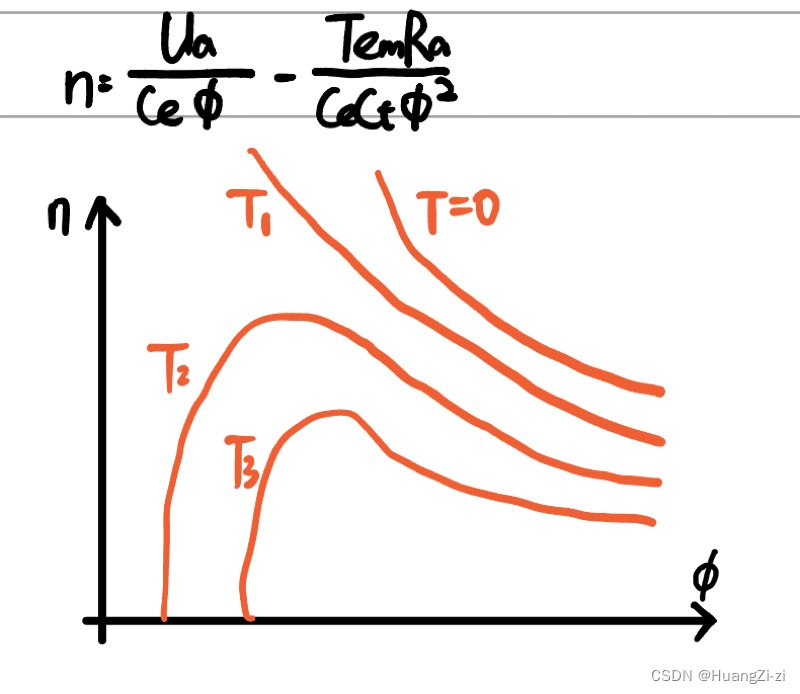
( T 3 > T 2 > T 1 T_3>T_2>T_1 T3>T2>T1)
调节特性是非线性曲线。
磁场控制的优缺点
优点:
- 控制功率 U f I f U_fI_f UfIf小,可以控制大型电机
缺点:
- 只能弱磁调速(因为铁心的工作点已经设置在靠近饱和点的位置,因此控制时只能减弱磁场进行控制)
- 动态性能较差(调节特性是非线性的,难以精确控制)
改变电枢回路串电阻时的机械特性
改变电枢回路串连电阻的大小。这个方法很少用,所以甚至连调节特性都没有分析。
固定总电阻,画转速和转矩的关系
改变回路总电阻,画出机械特性族:
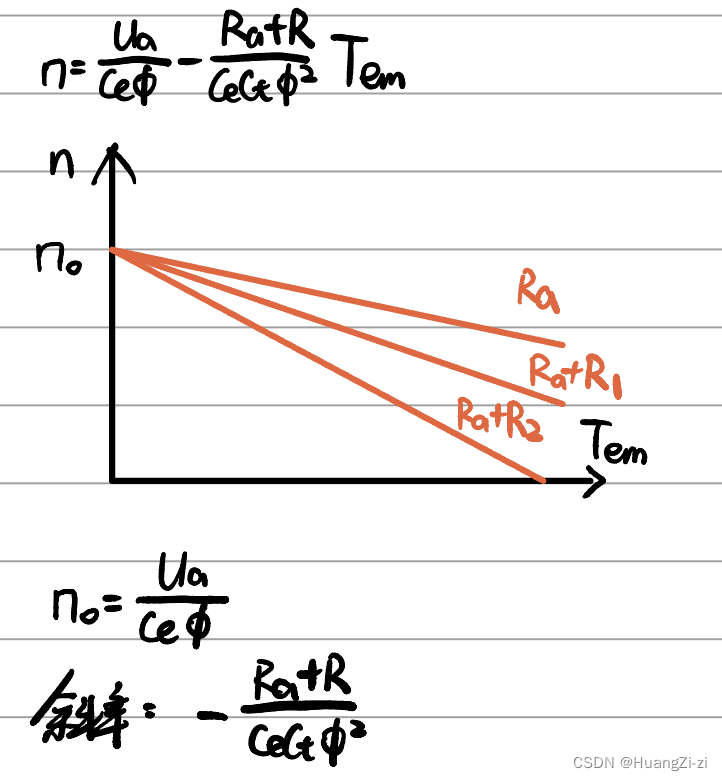
R越大,直线越陡。
理想空载转速不变。
机械特性族是放射形直线。
改变电枢回路串电阻的缺点
- 功率损耗较大
- 有级调速
稳态运行时的功率关系

铜耗
P
c
u
=
I
a
2
R
a
P_{cu}=I_a^2R_a
Pcu=Ia2Ra就是通电后导线发热功率。
输出功率
P
2
=
T
2
ω
P_2=T_2\omega
P2=T2ω。这里忽略了阻转矩,
T
2
=
T
e
m
,
P
2
=
P
e
m
T_2=T_{em},P_2=P_{em}
T2=Tem,P2=Pem
无载损耗功率
P
0
P_0
P0,包括机械损耗和铁耗。如果计算阻转矩,则
P
1
=
P
c
u
+
P
0
+
P
2
P_1=P_{cu}+P_0+P_2
P1=Pcu+P0+P2
他励式直流电机的工作特性
他励式直流电机的工作特性:电枢电压Ua、励磁电流If为额定值,电动机带动机械负载时,转速n、转矩Tem、效率
η
\eta
η、输出功率P2与电枢电流Ia的关系。
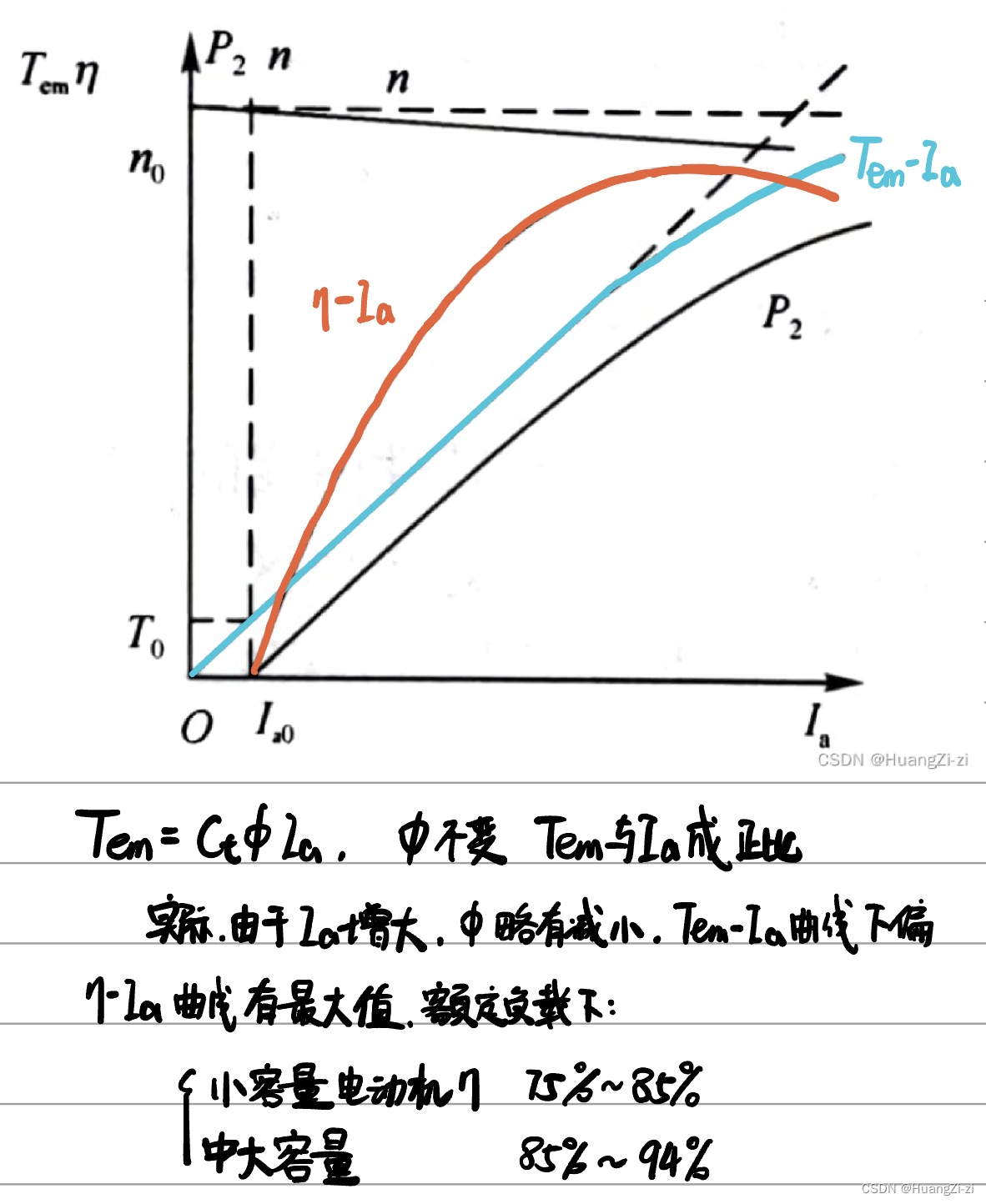
在这里需要讨论的一个话题是,励磁式电机在工作中断开励磁会发生什么:

飞车状态,电机转速过快,有可能导致离心力过大损坏电枢元件。
停车状态,停转后电枢电流 = 堵转电流,电流过大可能烧毁电枢元件。
因此尤其要注意,在工作过程中不能够断开励磁。而电机启动时,应该先接通励磁,在接通电枢。停止时应先切断电枢再切断励磁。
直流电机的启动
启动:直流电机接通电源后,转速从0达到稳定转速的过程。
启动要求启动转矩足够大,且启动电流限制在允许范围内,并让启动时间较短。
启动瞬间,n=0, I s t = U R a I_{st}=\displaystyle{\frac{U}{R_a}} Ist=RaU很大,约等于10~12倍额定电流,因此不能直接接电源,需要采取一定的启动方式。
降电压启动
也就是从较低的电压开始,逐渐提高电枢电压,直到额定电压,达到正常工作点。
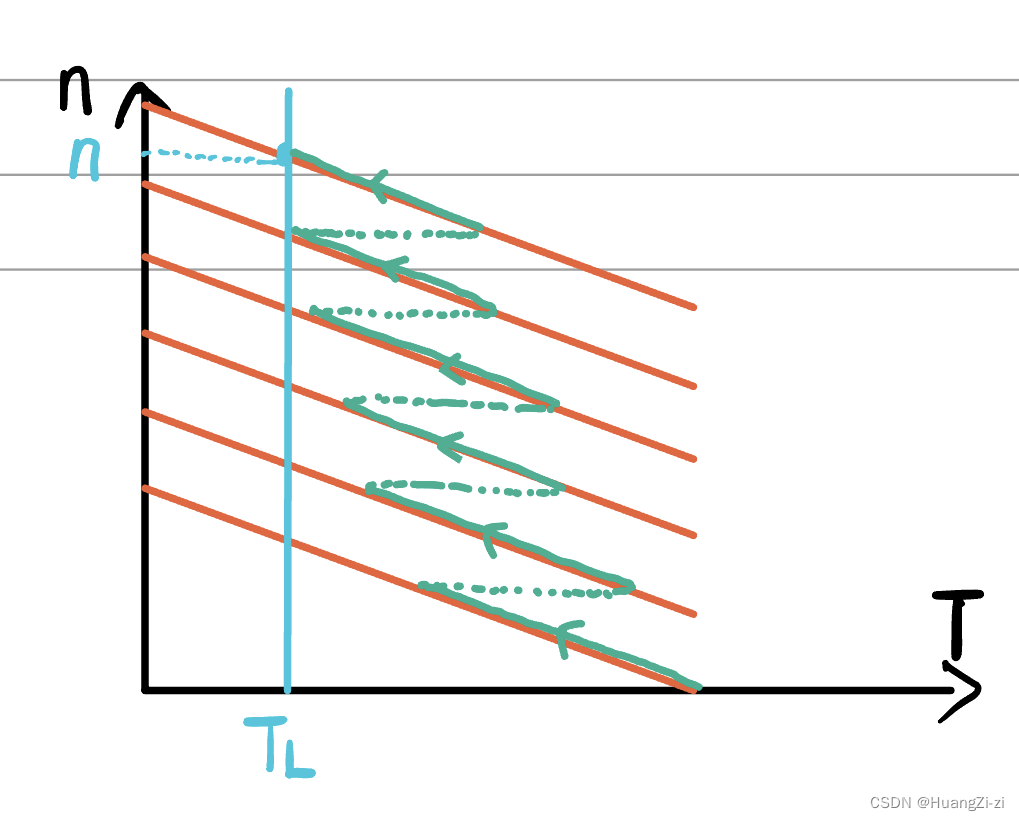
启动过程用绿色线表示。
这样启动电流
I
s
t
=
U
1
R
a
I_{st}=\frac{U_1}{R_a}
Ist=RaU1,只要合理控制第一次加的电压U1,就可以避免产生大电流。
电枢回路串电阻启动
也就是先在电枢回路串入大电阻,逐渐减小电阻直到为0,到达正常工作点。
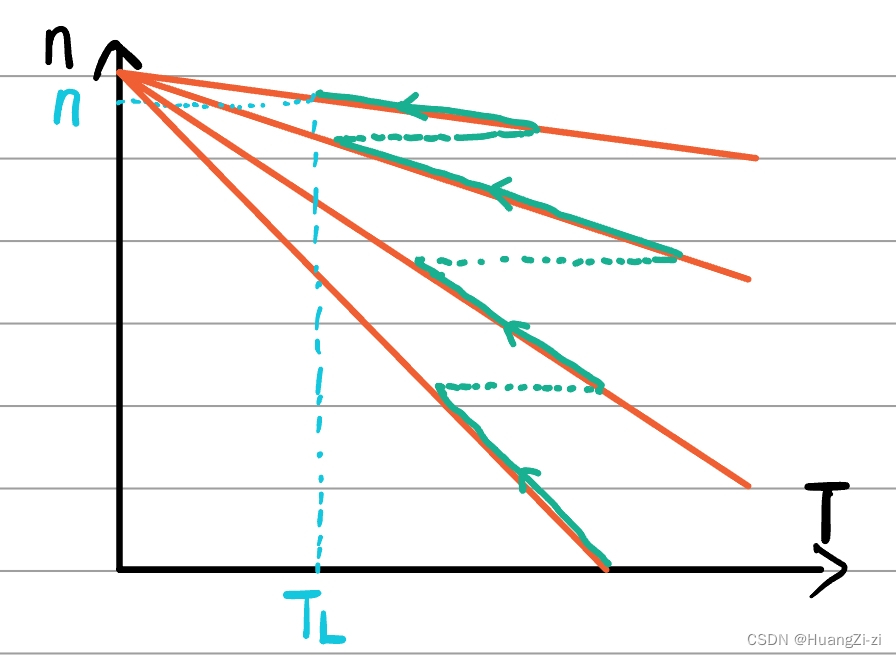
启动的过程用绿色线表示。
这样启动电流就变成了
I
s
t
=
U
a
R
a
+
R
I_{st}=\frac{U_a}{R_a+R}
Ist=Ra+RUa,只要合理控制第一次接入的R大小,也可以避免产生大电流。
电机稳定运行的条件
稳定运行:假设电机转速为n,当受到某种扰动,转速发生变化。当扰动消失后,电机能够回复到转速n,则称这个运行状态为稳定运行状态,用 T e m = T L \bold{T_{em}=T_L} Tem=TL和n表示
电机能否稳定运行,与所带负载的特性有关。
负载的转矩特性
负载转速
n
n
n与负载转矩
T
L
T_L
TL之间的关系。
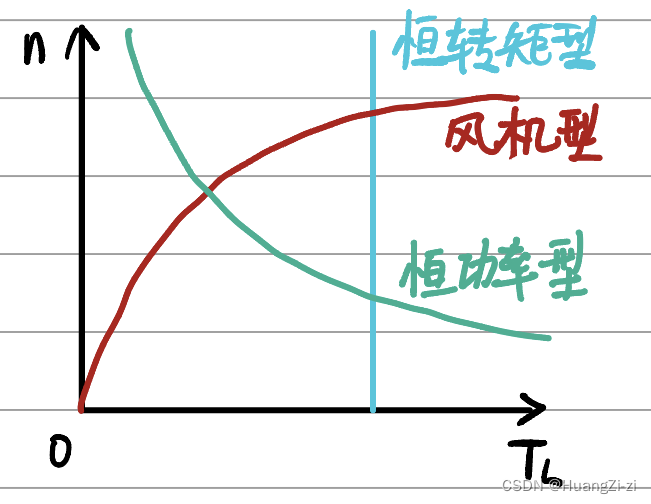
- 恒转矩型:负载转矩与转速无关, T L = c o n s t T_L=const TL=const
- 风机型:也叫泵类负载, T L ∝ n 2 T_L\propto n^2 TL∝n2
- 恒功率负载:负载功率恒定,
P L = T L ω = c o n s t P_L=T_L\omega=const PL=TLω=const
当电机的机械特性是下垂的:

也就是随着转矩增大,转速降低。目前我们接触的几种电机调节方法都是下垂的。
当电机的机械特性是上翘的:
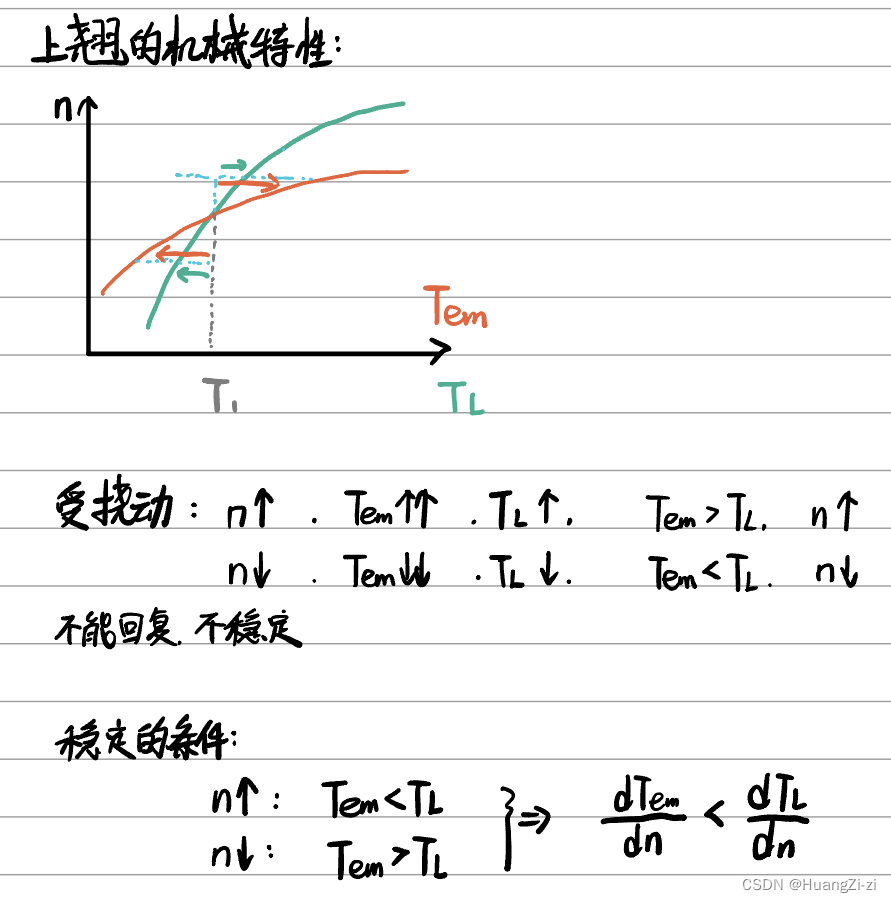
在图示的情况下是不能稳定的。但如果机械特性线比负载特性线更陡,就可以稳定了。
稳定运行的条件
在 T e m = T L T_{em}=T_L Tem=TL处,满足 d T e m d n < d T L d n \displaystyle{\frac{dT_{em}}{dn}<\frac{dT_L}{dn}} dndTem<dndTL
「补充」以上分析是基于转速改变引起的扰动。而实际情况下,干扰也可能是由于电压改变引起的。也就是机械特性线会发生移动:
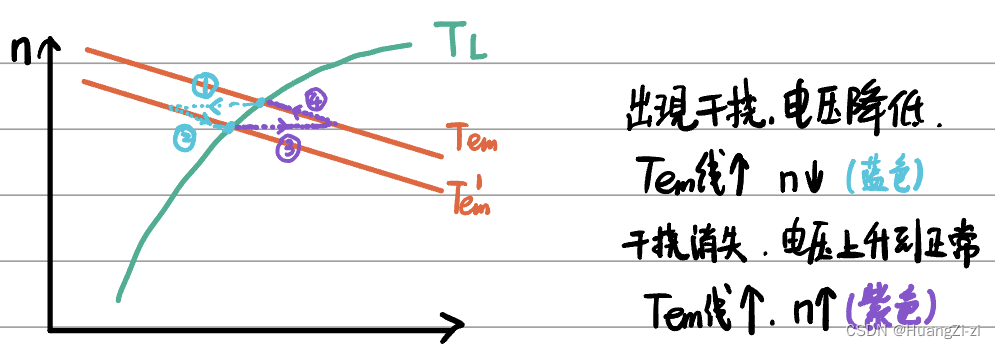
调速方式与负载类型的配合
调速方式有:
- 恒转矩调速
包括降压调速(电枢控制)、电枢回路串电阻调速
在整个调速范围内输出转矩为常数,输出功率与转速成正比 - 恒功率调速
包括弱磁调速(磁场控制)
在整个调速范围内输出功率为常数,转矩与转速成反比
- 恒转矩负载采用恒转矩调速
- 恒功率负载采用恒功率调速
直流电动机的四种工作状态
1 电动机状态
就是之前分析研究了很久的作为电动机工作的状态。
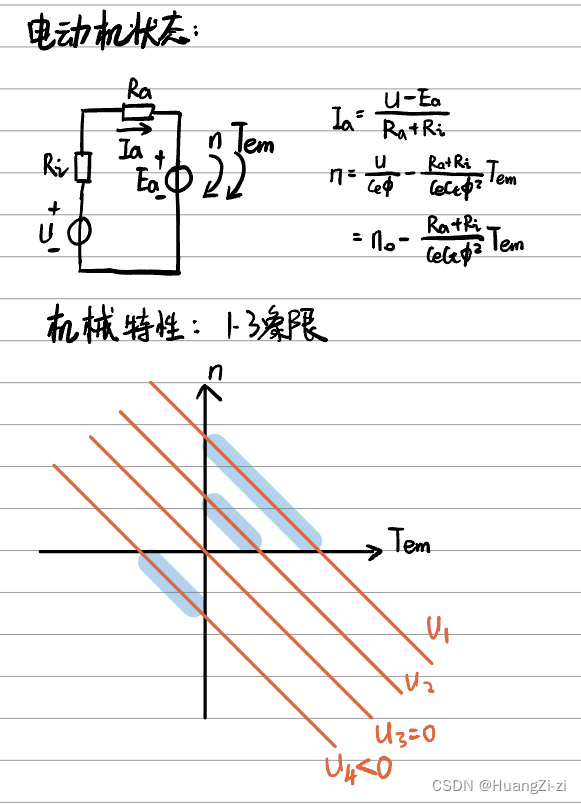
外加电压大于电枢感应电势,二者方向相反
电流为正,小于堵转电流,与外加电压方向匹配
电磁转矩方向和转速相同,转速低于空载转速
电能转化为机械能
2 发电机状态
也叫回馈状态。是指直流电机作为电动机工作的某一个状态,并不是作为发电机工作。

外加电压小于电枢感应电势,二者方向相反
电流为负,与感应电势方向匹配
电磁转矩方向和电机转速相反,转速高于理想空载转速。
机械能转化为电能
3 能耗制动状态
去掉外加电源。注意这里不是直接断开电源,而是保持了电枢回路。
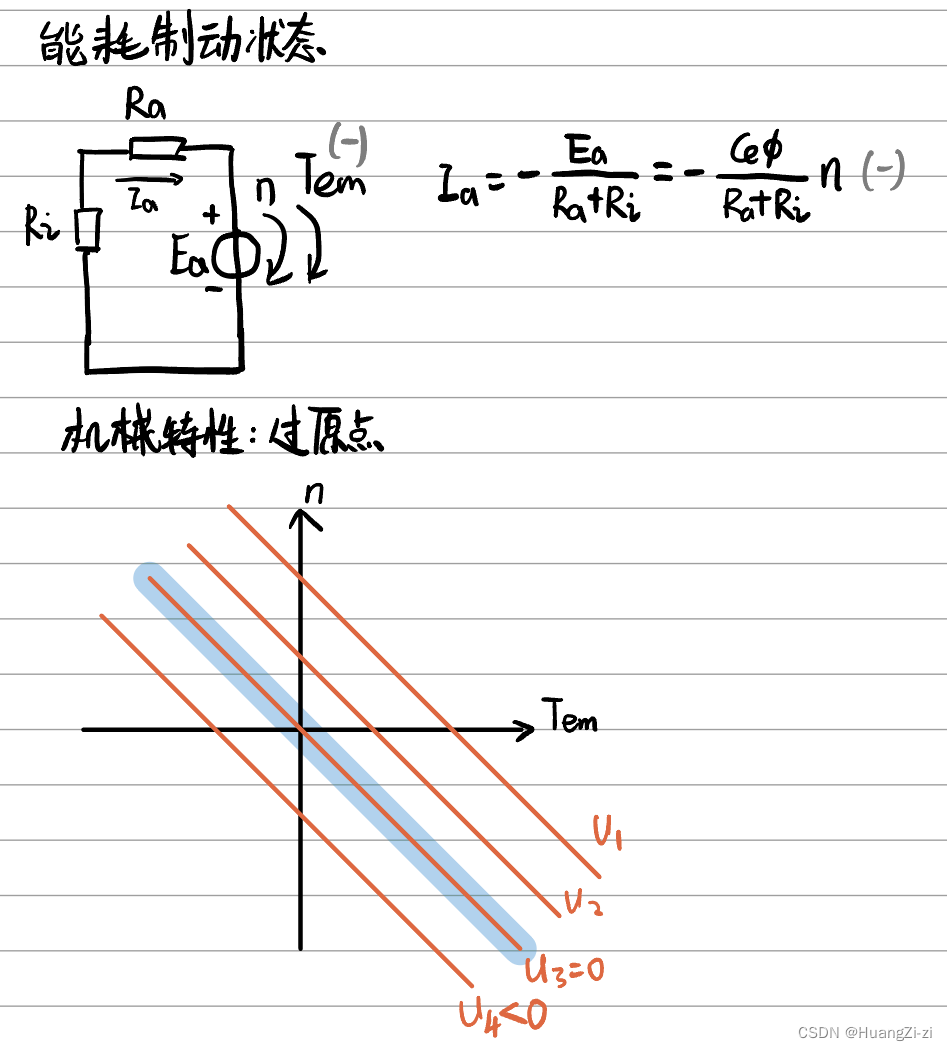
外加电压=0
电流为负,与感应电势方向匹配
电磁转矩方向和电机转速相反
机械能转化为电能继而转化为热能
能耗制动状态一般用在停转的过程中。除了去掉外加电源,还可以增加电枢回路的串连电阻,加快制动。
4 反接制动状态
输入电压U反向:
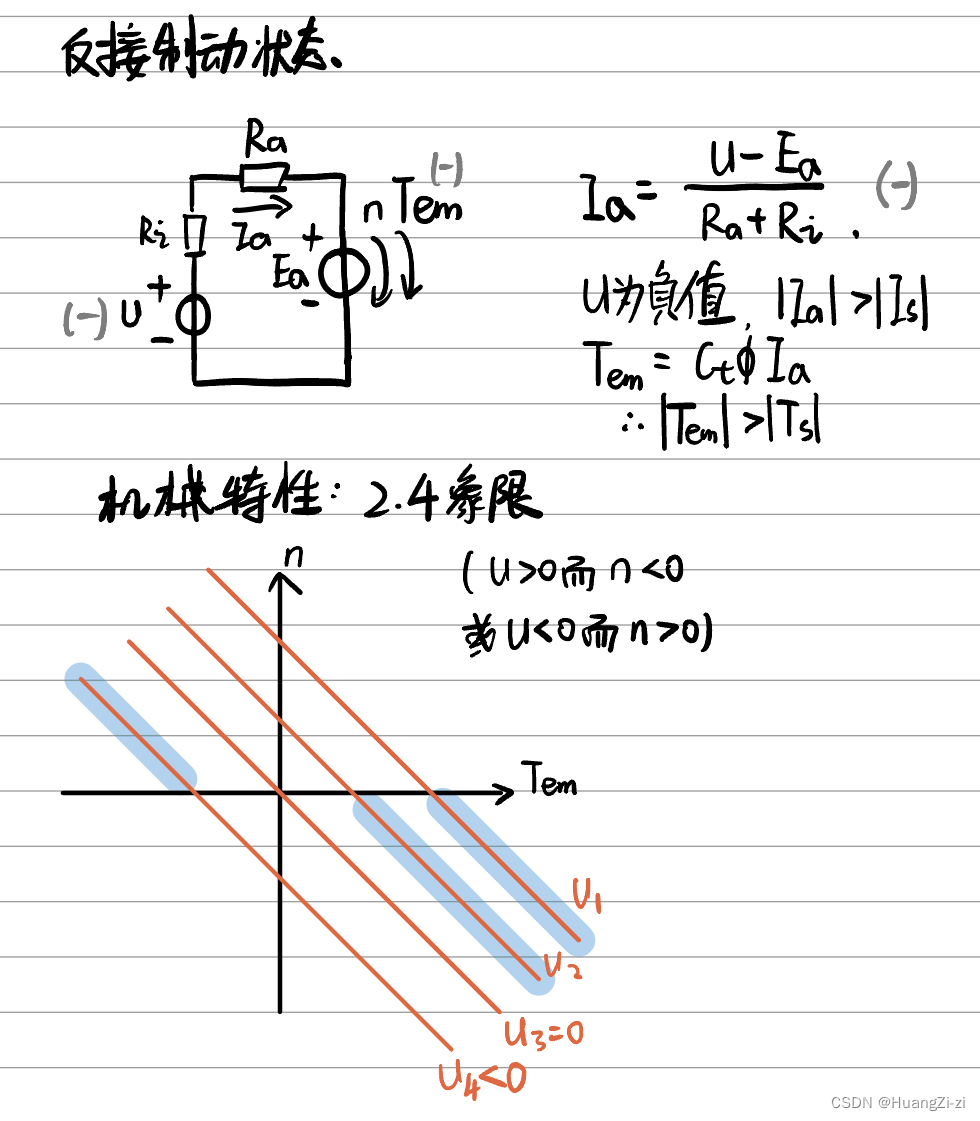
外加电压与感应电势同向
电流为负,且大于堵转电流。与外电压、感应电动势方向匹配
电磁转矩与转速方向相反。且大于堵转转矩
电能和机械能转变为热能
工作状态分析

这里以调速为例。电机经过了发电机状态和电动机状态。依次类推:在控制过程中,一台电动机至少包含两个状态
发电机状态、能耗制动状态、反接制动状态,电磁转矩方向都与转速方向相反,是制动转矩,加快减速过程。
直流电机的动态特性
稳态运行:电动机在负载特性和机械特性的交点上恒速运行
过渡过程 \ 动态过程:电动机从一个稳态到另一个稳态的变化过程,电动机在交点以外的机械特性上运行
动态过程中电动机具有的特性就称作动态特性。在这里用方框图和传递函数来表达。
电枢控制时的动态特性
以Ua为输入, ω \omega ω(t)(角速度)为输出
这里用到了一些自控原理的知识。参考这里:自动控制原理学习笔记
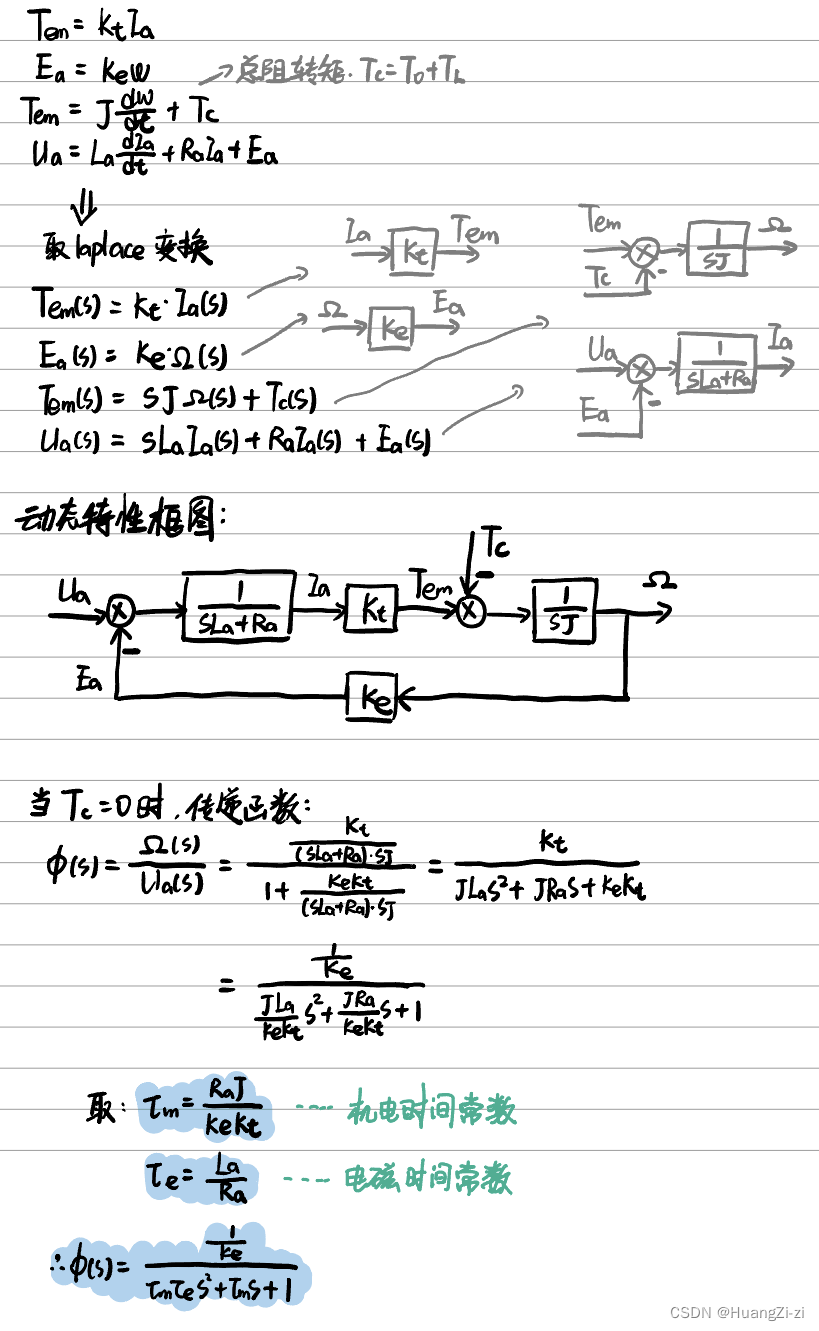
{
Φ
(
s
)
=
1
/
K
e
τ
m
τ
e
s
2
+
τ
m
s
+
1
τ
m
=
R
a
J
K
e
K
t
τ
e
=
L
a
R
a
\left \{ \begin{aligned} \displaystyle&\Phi(s)&=&\frac{1/K_e}{\tau_m\tau_es^2+\tau_ms+1}\\\\ &\tau_m&=&\frac{R_aJ}{K_eK_t}\\\\ &\tau_e&=&\frac{L_a}{R_a} \end{aligned} \right.
⎩
⎨
⎧Φ(s)τmτe===τmτes2+τms+11/KeKeKtRaJRaLa
提出了两个常数,分别是机电时间常数和电磁时间常数。
一般情况下有
τ
m
>
10
τ
e
\tau_m>10\tau_e
τm>10τe,因此传递函数也可以表示为:
Ω
(
s
)
U
a
(
s
)
=
1
/
K
e
(
τ
m
s
+
1
)
(
τ
e
s
+
1
)
\displaystyle \frac{\Omega(s)}{U_a(s)}=\frac{1/K_e}{(\tau_ms+1)(\tau_es+1)}
Ua(s)Ω(s)=(τms+1)(τes+1)1/Ke
当
τ
e
\tau_e
τe很小的时候,传递函数还可以表示为:
Ω
(
s
)
U
a
(
s
)
=
1
/
K
e
(
τ
m
s
+
1
)
\displaystyle \frac{\Omega(s)}{U_a(s)}=\frac{1/K_e}{(\tau_ms+1)}
Ua(s)Ω(s)=(τms+1)1/Ke,这就变成了一个一阶系统。
时间响应如图:
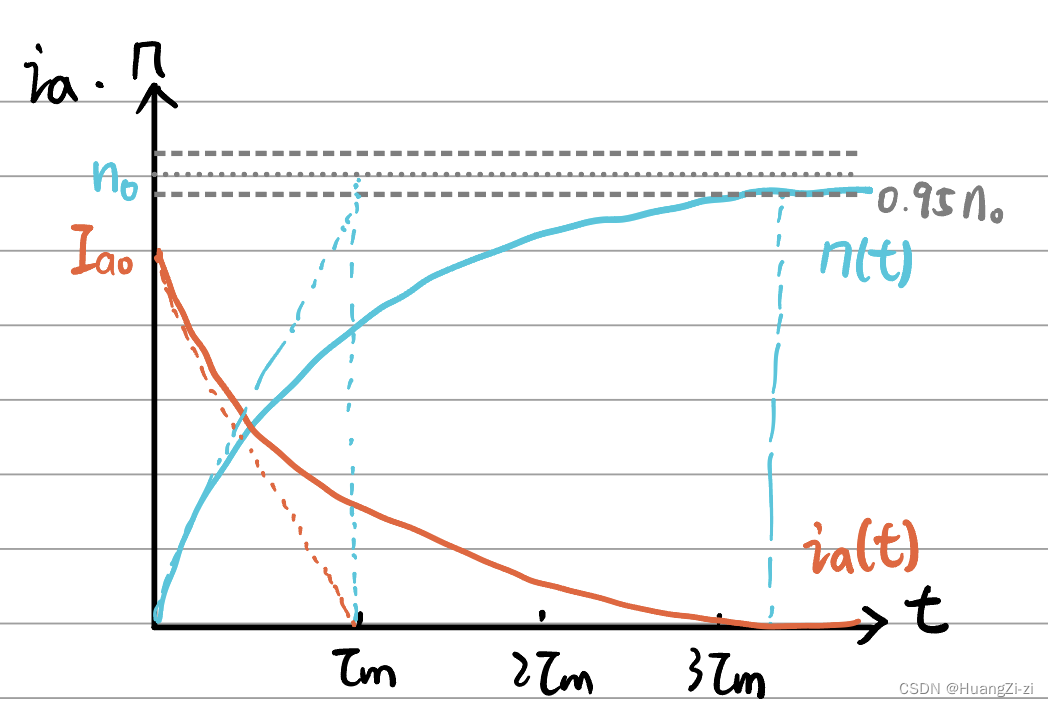
τ m \tau_m τm和静态特性的关系
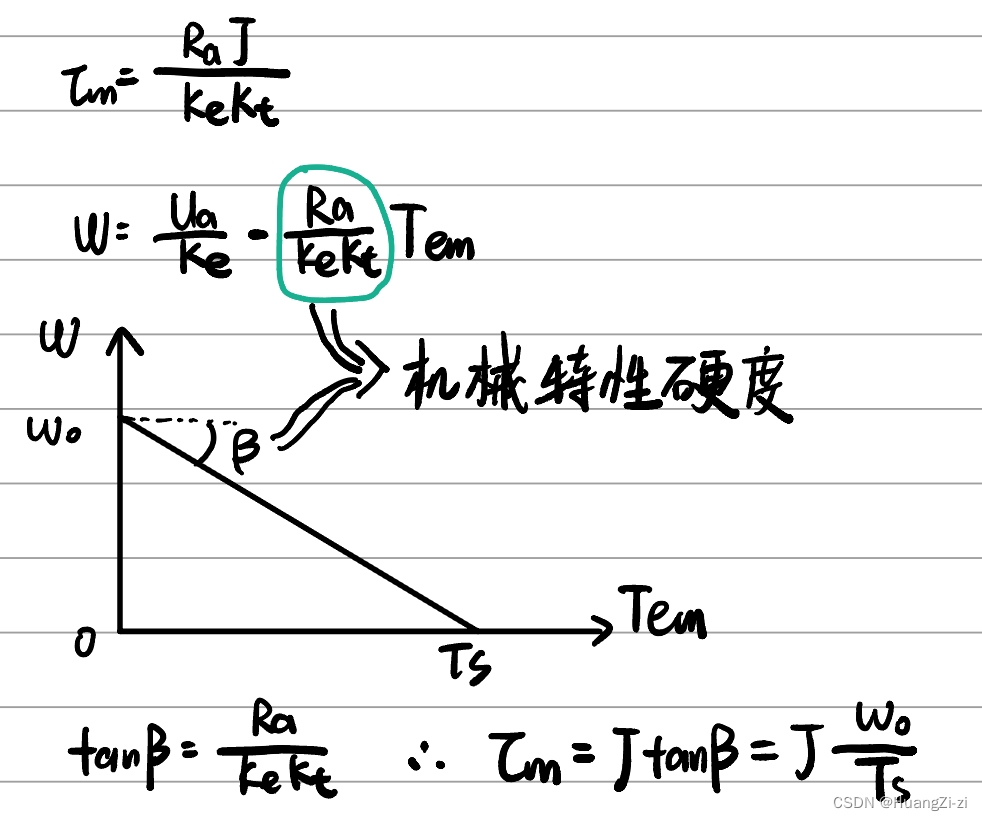
机电时间常数与机械特性斜率成正比。机械特性硬度越大,直线越平,机电时间常数越小,响应越快。
控制回路电阻Ra在分子,即减小内阻有利于快速响应
转动惯量J在分子,即负载的转动惯量将增大时间常数
结构参数
K
e
K
t
=
p
2
N
2
ϕ
2
120
π
a
2
K_eK_t=\frac{p^2N^2\phi^2}{120\pi a^2}
KeKt=120πa2p2N2ϕ2在分母,为减小时间常数,可以采用合理的绕组形式(减少并联支路数a)、选择恰当的磁极对数(增大p)、适当提高每极下的磁通(增大
ϕ
\phi
ϕ)
例题:

其实公式就这么几个。主要注意一些特殊的工作状态就可以。比如堵转和启动,n=0,Ea=0,空载Tem=Tf
以Ua为输入, θ \theta θ(t)(角位移)为输出
直观理解,角位移=角速度积分。所以只需要给前面的方框图加一个积分环节就ok

以Ia为输入
控制系统采用电流源性质的功放。

不同在于这里需要根据总阻转矩求粘滞系数。
磁场控制时的动态特性
这个就不细推了。在假设电枢电流不变的情况下:
Ω
(
s
)
U
f
(
s
)
=
K
t
(
J
s
+
K
c
)
(
L
f
s
+
R
f
)
=
K
t
/
K
c
R
f
(
τ
m
s
+
1
)
(
τ
e
s
+
1
)
\displaystyle \frac{\Omega(s)}{U_f(s)}=\frac{K_t}{(Js+K_c)(L_fs+R_f)}=\frac{K_t/K_cR_f}{(\tau_ms+1)(\tau_es+1)}
Uf(s)Ω(s)=(Js+Kc)(Lfs+Rf)Kt=(τms+1)(τes+1)Kt/KcRf
其中Uf为励磁电压,If为励磁电流,Lf为励磁线圈电感,
τ
m
=
J
K
c
\tau_m=\frac{J}{K_c}
τm=KcJ为机械时间常数,
τ
e
=
L
f
R
f
\tau_e=\frac{L_f}{R_f}
τe=RfLf为电磁时间常数
磁场控制时电机的非线性非常严重,所以一般不这样控制。而且实际很难保证电枢电流不变,所以这个传递函数也不准确。
控制系统中应用的直流电动机
这些电动机的工作原理和之前介绍的完全一样。只是为了适配控制系统,专门做出了一些优化。这几个种类的电机了解就可以。
直流伺服电机
就是专门伺服控制系统设计和制造的一种电机。伺服控制系统需要根据输入快速调整输出,因此直流伺服电机具有响应快速的特点。
除了一般直流电动机具有的稳定性好,可控性好等优点,还有:
- 将电枢做得细长,转动惯量小
- 换向性能优良,能承受大的瞬时电流
- 机械强度高,能承受大的瞬时转矩
- 电刷放置在几何中性面,保证正反转时特性对称
当然也会有缺点:
- KeKt小,转矩小
- 低速运转不平稳
直流伺服电机也分为传统型直流伺服电机、低惯量型直流伺服电机、宽调速直流伺服电机。
传统型直流伺服电机
结构与普通直流电机相似(有槽),但是转子细长。
分为电磁式和永磁式。
低惯量型直流伺服电机
转子更加细长,甚至转动部分没有铁心 ——(减小转子转动惯量,减小机电时间常数)
铁心没有齿槽 ——(减小力矩波动,使低速运转平稳)
电枢绕组与铁心分离 ——(增大磁阻,减小电枢电感,进而提高换向性能)
低惯量型直流伺服电机,还可以向下细分:
无槽电枢直流伺服电机:
电枢铁心无槽,电枢绕组固定在铁心表面,冷却效果好。气隙大,电感小。
盘式电枢直流伺服电动机:
转子是圆盘形,电流径向流过圆盘表面,导体绕组兼做换向器。
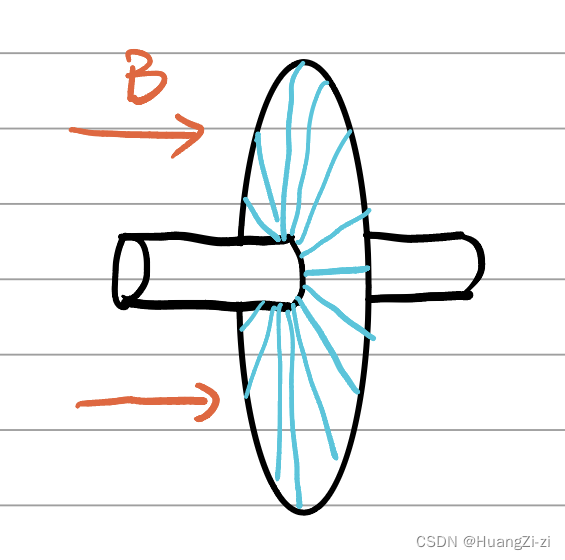
图有点抽象,蓝色是绕组。绕组的径向段为有效长度。这种电机特别使用与轴向尺寸小的场合。
空心杯电枢直流伺服电动机:
当下比较新兴也比较火热的一种电动机。也是低惯量电动机中性能最好的一种。电枢做成杯形,转子无铁心。分为内磁式和外磁式。其中外磁式是指外定子为永磁体,内定子为软磁材料。
外磁式空心杯电枢直流伺服电动机的机电时间常数是各种交直流电动机中最小的。

宽调速直流伺服电机
这是直流伺服电动机的第三种。
之前说直流伺服电机有低转速运转不平稳的现象,是因为转速低时,电枢电压和电枢反电势都很小,相应受到齿槽效应造成的影响,电势波动增大,导致电流及电磁转矩波动较大。此外,电动机的频率响应为低频通,高频衰减,因此在低转速时电势、转矩波动对电机的影响大于高转速时。
不同于之前通过无槽铁心降低波动,宽调速直流伺服电机通过增加磁极对数、齿槽数来增加低速时稳定性
宽调速直流伺服电机也分为永磁式和励磁式。而永磁式一般不安装换向极和补偿绕组,所以机构上会有一点点不同。
为了降低成本,一般采用铁氧体做磁极材料,而为了弥补铁氧体剩磁太小的问题,增加侧磁极(绿色)。
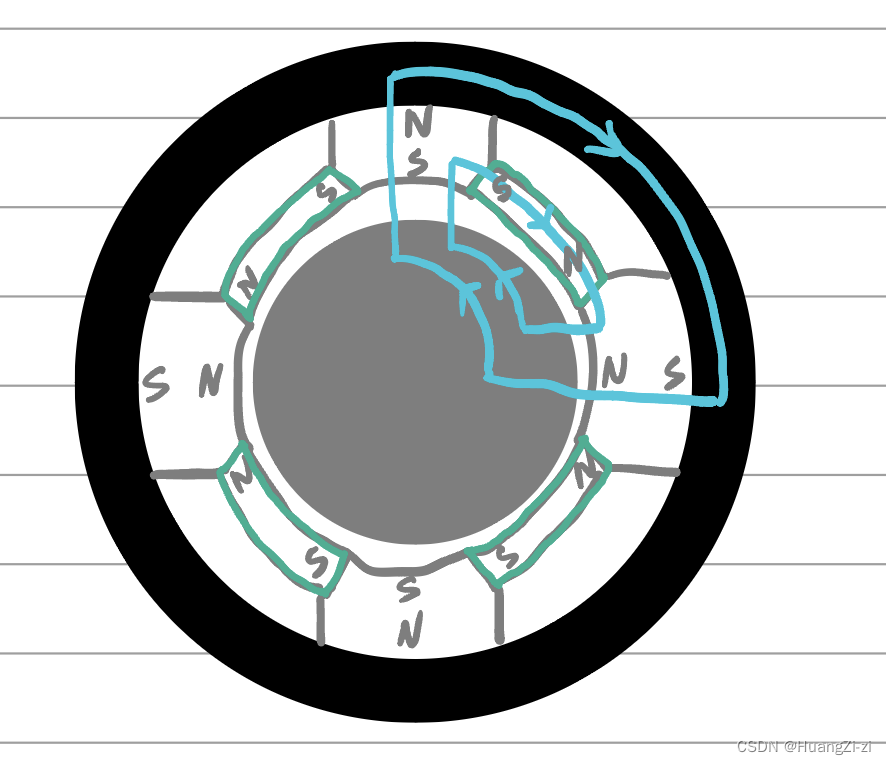
宽调速直流伺服电机转矩大,调速范围宽,可以与负载同轴连接。转子转动惯量大,可以忽略负载的折算惯量,使控制器适用性广。热容量大,允许较长时间过载工作。
这种电动机广泛用于各种机床、雷达天线驱动等场合。
直流力矩电动机
之前介绍的电机都属于高速电机,额定转速几百上千转,同等功率下力矩小,因此常需要搭配减速器使用。
而直流力矩电机是一种低转速、大转矩的直流电动机,可以直接带动负载工作。
由于减少了机械减速器,使得系统响应迅速、精度高、线性度好,运行可靠。
而直流力矩电动机本身的特点还有:

值得一提的是,直流力矩电动机是我们接触的电机里唯一一种使用单波绕组的电机。通过这种绕制方法使并联支路对数a更小。
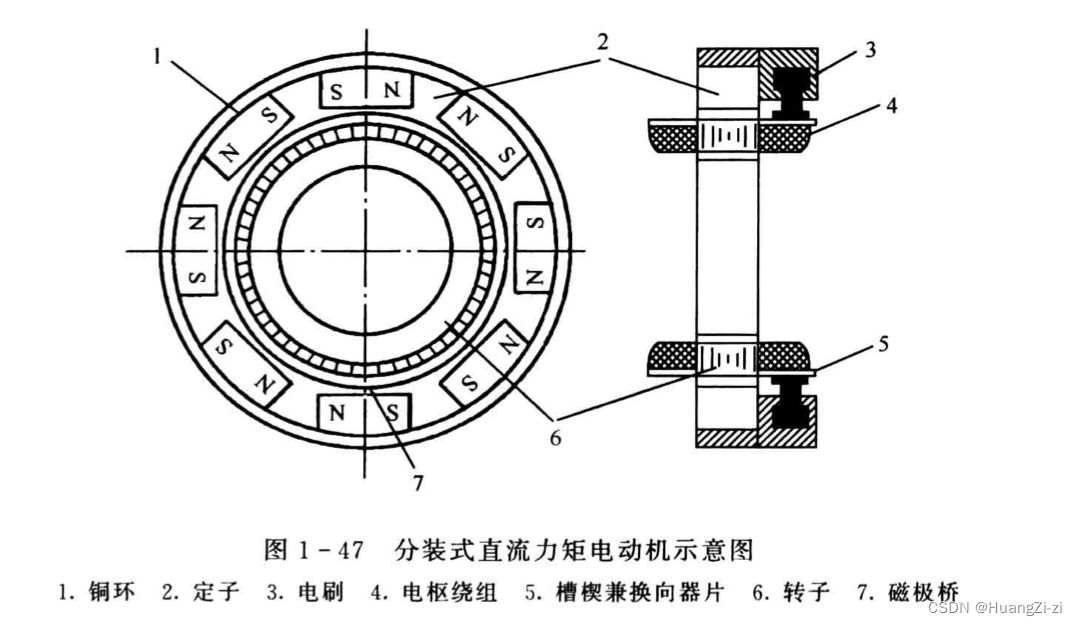
「图源:自动控制元件及线路_梅晓榕」
这里的磁极桥作用是使气隙中磁场更均匀。
分装式也就是工厂提供转子、定子、刷架,供用户自行转配,以便和其他部件组合。
有限转角直流力矩电动机
最大的特征就是没有换向器。
转子是一个简单的磁极,而绕组在定子上。电枢(定子)又分齿槽结构和环形结构。
这里只画了环形。

在一定的转角范围内,力矩不变。工作范围有限。
没有电刷,没有其带来的摩擦、火花,寿命长。
能在低速和堵转情况下长期正常工作,转矩大,响应快。
传递函数和普通直流电机相同。
这种电机常用在小转角的高精度控制系统中,比如各种稳定平台、仪表指针、驱动记录笔等。
直流电机的选型原则
电机选型需要考虑到额因素很多,这里只是大概介绍一下:
- 转矩——额定转矩和峰值转矩
- 转速
- 功率
- 尺寸和重量