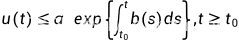整理自一个知乎大佬的回答

Cauchy-Schwarz积分不等式

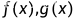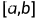在上可积,有:

取等号的充要条件是存在常数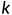,使得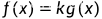

Hölder 积分不等式

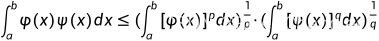
Minkowski 积分不等式

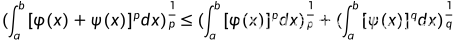
Chebyshev 积分不等式

设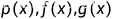在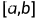上是连续函数,并且在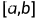上单调递增,则

Kantorovich 积分不等式

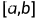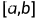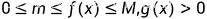设函数均在区间上可积,且在上满足,则

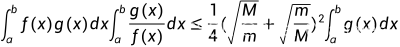
Jensen 积分不等式

若函数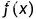为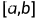上的可积函数,且,又是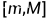上的连续下凹函数,则有:

若是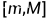上的连续上凸函数时,上式中的不等号相反.

Hadamard 积分不等式

设是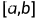上的凸函数,

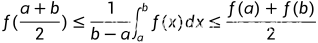
流行积分不等式

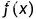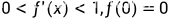设是上的可微函数,且当时,则

Dirichlet 核积分不等式

Dirichlet 核:

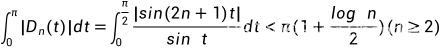
Favard 积分不等式

若函数是一个非负凹函数,则有:

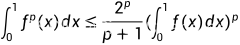
Wirtinger 积分不等式

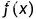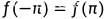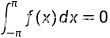设是上的连续可微函数,且,若,则有

当且仅当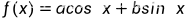等号成立

Hardy 积分不等式

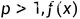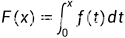设在上非负可积,则有

当且仅当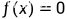时等号成立

Carleman 积分不等式

设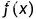可积,则有

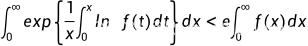
Carlson 积分不等式

设则有

lyengar 积分不等式

设在区间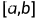上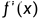的绝对值有界,且,则有

Zmorovich 积分不等式

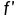在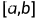上绝对连续,则

Gronwall 积分不等式

设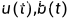是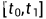上非负连续函数,并满足,

则