离散数学，半群性质的证明，群，群的性质，子群

news2024/12/25 9:45:52

目录

1.半群性质的证明

半群的性质 

定理5-3.2证明 

定理5-3.3证明 

半群的性质 

定理5-3.4证明 

例子 

2.群 

群是每个元素都可逆的独异点 

例子 

有限群，阶数，无限群，平凡群 

3.群的性质 

群中不可能有零元 

群中任一元素逆元唯一 

群中a*x=b方程解唯一 

消去律 

置换 

群中的幂 

例子 

4.子群

平凡子群 

子群判定定理一 

子群判定定理二 

子群判定定理三 

例子 

习题 

1.半群性质的证明

半群的性质 

6156e1dafda5480d8128ea027cf2d99b.png

定理5-3.2证明 

2c7140d1290b472abbd0385ae56f5ad4.png

定理5-3.3证明 

7b9a8b052eb24d869e03b45e560ab774.png

078e29fabb404b8594fbddd386d8fc1d.png

半群的性质 

68df06e9fc904d5c85a0c40f6c15bddd.png

定理5-3.4证明 

c05fa1b88fee40829be3f6c3a040ff04.png

例子 

198646f72388400db80f13f6d4534777.png

939c4016f99b4c05976abb57bb404cb0.png

be1a56d8021a4cd0b391ec4c3acbfecf.png

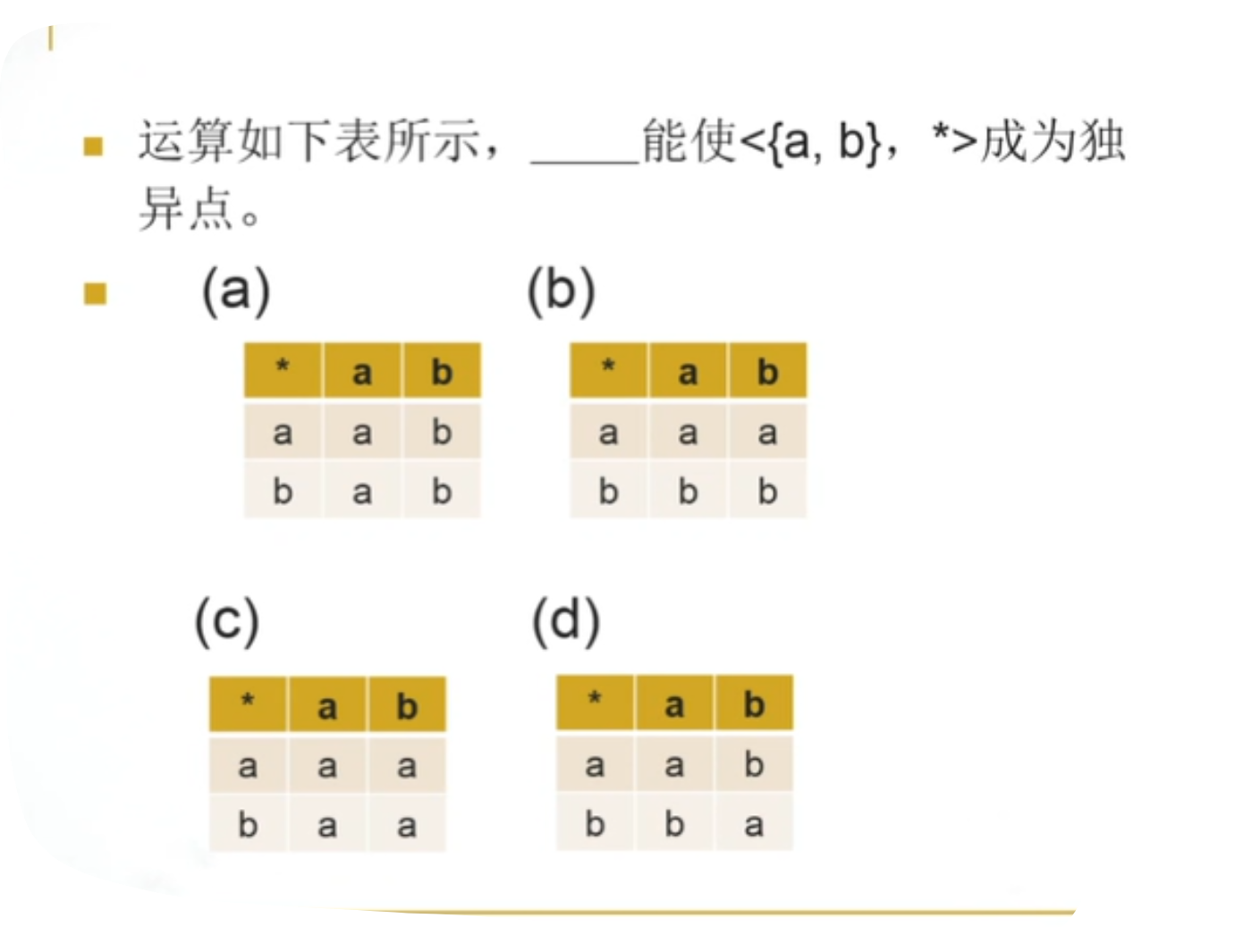
13154f4eade04d3dad72a237e7b7a8dd.png

2.群 

4a8febb0acf34c1cabdeae92fdd41636.png

群是每个元素都可逆的独异点 

f734af7c82c544b79952675225135a88.png

例子 

257e4b3952254cada90284212ffdfc90.png

8107269774f1478d86597bb24630fec1.png

167ae4e04a06476d877e44a4b3943332.png

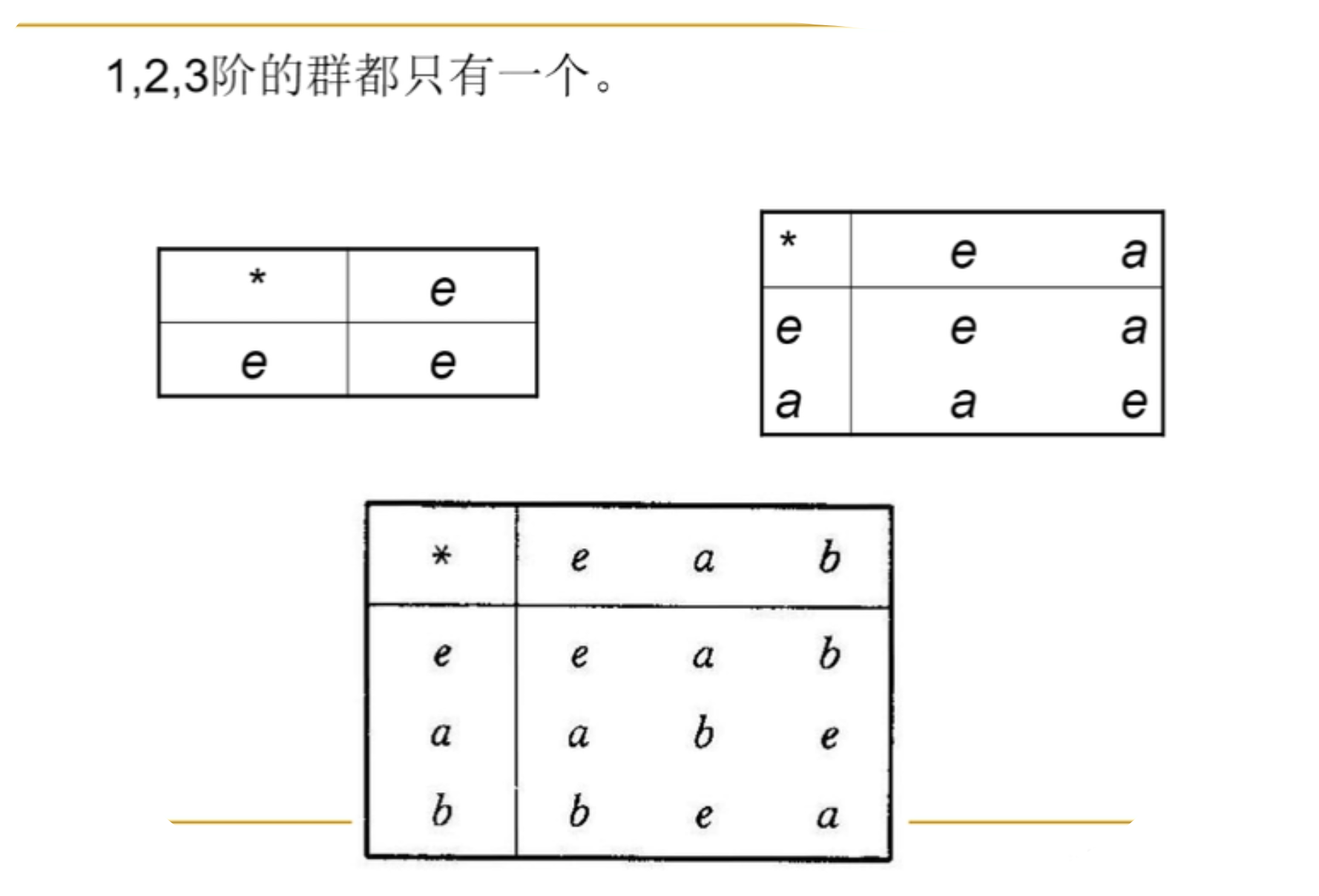
有限群，阶数，无限群，平凡群 

eff9ea0617ff41e98898fe954ff0b35c.png

3.群的性质 

d55386f3aea84478aa3715e2d2686cb0.png

2f75fd5a8f054697abeede441bd3f285.png

群中不可能有零元 

be28ecaa722e47b4a16eae12dba766bd.png

群中任一元素逆元唯一 

c3d20df9ef444831aca0d3bfc02801b9.png

群中a*x=b方程解唯一 

87a6cdc1052441fa9b7c49ccf1ebe59e.png

消去律 

497f1fe992b14a939c1f39650aeaee4f.png

置换 

aed5ef381b3e4575ac58260359b7cf4a.png

群中的幂 

4ac7e86ec09f4e33a4d1501ae7708c40.png

ab6b40e0a7b34da994a03ca3cfe8bb4b.png

7fb7fa833dcb4632a152c15e61f9da95.png

例子 

fd79d9c7193f41879e089b4ba91dbd8a.png

86d25f9a36e14860896dbdb87f711a88.png

4f6176d3d7334a81aa94675c4ba26261.png

8bb1fb4209f14bf4ad8a2ef6b84f0db7.png

4.子群

平凡子群 

99032882462d4081a9d09d64ba8147aa.png

子群判定定理一 

e8ff399571ca47918c44e329b24a882c.png

f1f3ecf90e8e4dc9b5018db3358c3047.png

a48c92d179574d9d9cf00c4569747f48.png

子群判定定理二 

a07fcffbbc8c45ed9ec32e152cd4bd12.png

7540b28154154b79bb4a994ed8769eab.png

子群判定定理三 

 531195968b16498cb72739ebb573576c.png

51c03319b98a4e0e92bc17731b4f3b10.png

例子 

bfb0f6b4d70f4f758ddb3df079e75f73.png

64339afc06df45fd89e9988def430880.png

ffd32cc42b7447238e6111f7b04647fa.png

习题 

4c6b56e3972446e1b59a1ec9e79b7fc0.png

20f65d2b55c9462496d8e38d944a18ba.png

1ea220f5d749431f9ebec88fff53da32.png

374f856602484cd89fccd8d0be917c82.png

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1937034.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Paypal个人支付申请及沙箱测试配置

Paypal个人支付申请及沙箱测试配置

目录 一. 申请paypal账号二. Sanbox 测试配置申请买家Account申请卖家AccountSandbox的Client ID及密钥申请Live的Client ID及密钥申请IPN回调设置 一. 申请paypal账号 浏览器输入https://www.paypal.com, 单击注册按钮 2. 我这里申请个人账户，如果你需要企业账户&…
阅读更多...
如何提升EVs应用潜力？EVs与工程化材料的结合！

如何提升EVs应用潜力？EVs与工程化材料的结合！

细胞外囊泡 (EVs)作为细胞间通讯的重要载体，在组织工程和再生医学中具有巨大的应用潜力。然而，EVs在体内的半衰期很短，难以有效地到达靶组织并发挥其生物学功能。因此，如何控制EVs的释放和保留成为实现其临床应用的关键。近年来&a…
阅读更多...
智慧旅游平台小程序的设计

智慧旅游平台小程序的设计

管理员账户功能包括：系统首页，个人中心，用户管理，景点分类管理，旅游景点管理，景区活动管理，留言板管理，系统管理 微信端账号功能包括：系统首页，旅游景点&…
阅读更多...
(七)原生js案例之评分功能

(七)原生js案例之评分功能

业务开发中，评分组件基本都是用element,antd这些框架的已经给我们封装好了现成的。现在手写一个原生的评分组件 效果 代码实现 必要的css .rating {width: 600px;margin: 60px auto;text-align: center;}.rating img {width: 30px;height: 30px;cursor: pointer…
阅读更多...
uniapp上传功能用uni-file-picker实现

uniapp上传功能用uni-file-picker实现

文章目录 html代码功能实现css样式代码 html代码 <uni-file-pickerselect"onFileSelected"cancel"onFilePickerCancel"limit"1"class"weightPage-upload-but"file-mediatype"image"></uni-file-picker><imag…
阅读更多...
Java记事本工具Notepad++

Java记事本工具Notepad++

常见的高级记事本 Editplus、Notepad、Sublime Notepad软件的安装和使用 安装&#xff1a;傻瓜式安装 1、选择中文-->【OK】 2、点击【下一步】 3、协议点击【我接受】 4、选择安装路径-->【下一步】 5、点击【下一步】 6、最后点击【安装】 7、将运行取消-->点击…
阅读更多...
机械学习—零基础学习日志（高数06——函数特性）

机械学习—零基础学习日志（高数06——函数特性）

零基础为了学人工智能&#xff0c;真的开始复习高数 函数的性质&#xff0c;开始新的学习&#xff01; 有界性&#xff1a; 解法放这里&#xff1a; 证明有界&#xff0c;其实内部的包含知识点很多。第一&#xff0c;如果有界&#xff0c;你需要证明函数在一定区间内&#xff…
阅读更多...
【体外诊断】ARM/X86+FPGA嵌入式计算机在免疫分析设备中的应用

【体外诊断】ARM/X86+FPGA嵌入式计算机在免疫分析设备中的应用

体外诊断 信迈提供基于Intel平台、AMD平台、NXP平台的核心板、2.5寸主板、Mini-ITX主板、4寸主板、PICO-ITX主板&#xff0c;以及嵌入式准系统等计算机硬件。产品支持GAHDMI等独立双显&#xff0c;提供丰富串口、USB、GPIO、PCIe扩展接口等I/O接口&#xff0c;扩展性强&#xf…
阅读更多...
pytorch学习（九）激活函数

pytorch学习（九）激活函数

1.pytorch常用激活函数如下&#xff1a; #ReLU激活函数 #Leaky ReLU激活函数 #Sigmoid激活函数 #Tanh激活函数 #Softmax激活函数 #Softplus2.代码 import torch.nn as nn import torch import numpy from torch.utils.tensorboard import SummaryWriterwriter SummaryWriter…
阅读更多...
buu做题(5)

buu做题(5)

目录 [GXYCTF2019]禁止套娃 方法一: 方法二: [NCTF2019]Fake XML cookbook [GXYCTF2019]禁止套娃 页面里啥也没有 使用dirsearch 扫一下目录 发现有 git 使用工具githack拉取源码 <?php include "flag.php"; echo "flag在哪里呢&#xff1f;<br&g…
阅读更多...
空间计算开发：Volu的集成开发工具包

空间计算开发：Volu的集成开发工具包

在空间计算技术迅速发展的今天，VR和AR项目的开发需求日益增长。Volu，一个面向空间计算赛道的开发者工具，正致力于简化这一过程。本文将深入探讨Volu如何通过其集成环境，为开发者提供一站式的解决方案。 一、定位：空间计算的得力助手 Volu定位为一个专为空间开发设计的集…
阅读更多...
亚马逊自养号测评系统：电商卖家的销量加速器

亚马逊自养号测评系统：电商卖家的销量加速器

搭建一套属于自己的测评系统&#xff0c;以实现批量优质账号的养成和自主掌控真实买家行为&#xff0c;对于电商卖家来说&#xff0c;无疑是一个极具吸引力和竞争力的选择。以下是对您提出的实现价值点的详细解析&#xff1a; 实现价值详细解析 1.全面掌控与灵活应对&#xf…
阅读更多...
Chromium CI/CD 之Jenkins实用指南2024-添加Windows节点（八）

Chromium CI/CD 之Jenkins实用指南2024-添加Windows节点（八）

1. 引言 在现代软件开发流程中&#xff0c;持续集成&#xff08;CI&#xff09;和持续交付&#xff08;CD&#xff09;已成为确保代码质量和加速发布周期的关键实践。Jenkins作为一款广泛应用的开源自动化服务器&#xff0c;通过其强大的插件生态系统和灵活的配置选项&#xf…
阅读更多...
Qt中的高分辨率及缩放处理

Qt中的高分辨率及缩放处理

写在前面 使用Qt开发界面客户端&#xff0c;需要考虑不同分辨率及缩放对UI界面的影响&#xff0c;否则会影响整体的交互使用。 问题 高分辨率/缩放设备上图片/图标模糊 若不考虑高分辨及缩放处理&#xff0c;在高分辨率/缩放设备上&#xff0c;软件中的图片、图标可能会出现…
阅读更多...
rimraf快速删除node_modules方法

rimraf快速删除node_modules方法

项目中&#xff0c;有时候会遇到下载依赖报错&#xff0c;然后想要删除node_modules再重新下载&#xff0c;但是有时候直接用yarn 或者npm install仍热不行&#xff0c;我们可以尽量用yran&#xff0c;因为npm 可能会自动下一些给一些包升级了&#xff0c;此时因为前面已经下过…
阅读更多...
【D3.js in Action 3 精译_020】2.6 用 D3 设置与修改元素样式 + 名人专访（Nadieh Bremer）+ 2.7 本章小结

【D3.js in Action 3 精译_020】2.6 用 D3 设置与修改元素样式 + 名人专访（Nadieh Bremer）+ 2.7 本章小结

当前内容所在位置 第一部分 D3.js 基础知识 第一章 D3.js 简介&#xff08;已完结&#xff09; 1.1 何为 D3.js&#xff1f;1.2 D3 生态系统——入门须知1.3 数据可视化最佳实践&#xff08;上&#xff09;1.3 数据可视化最佳实践&#xff08;下&#xff09;1.4 本章小结 第二章…
阅读更多...
Linux云计算 |【第一阶段】ENGINEER-DAY4

Linux云计算 |【第一阶段】ENGINEER-DAY4

主要内容&#xff1a; 配置Linux网络参数、配置静态主机名、查看/修改/激活/禁用网络连接、指定DNS、虚拟网络连接、虚拟机克隆、SSH客户端、SCP远程复制、SSH无密码验证&#xff08;SERVICE-DAY5&#xff09;、虚拟网络类型 一、网络参数配置 修改网卡配置文件主要是需要配置…
阅读更多...
Spring Authorization Server 自定义 OAuth2 密码模式返回数据结构优化

Spring Authorization Server 自定义 OAuth2 密码模式返回数据结构优化

前言 对接了自定义密码模式&#xff0c;但是返回的数据结构不符合要求 我们需要改成下面格式 开始 我假设你已经对接好了自定义密码功能&#xff0c;不会的话看下面文章 Spring Authorization Server 1.1 扩展实现 OAuth2 密码模式与 Spring Cloud 的整合实战&#xff08;上…
阅读更多...
23种设计模式之命令模式

23种设计模式之命令模式

命令模式 1、定义 命令模式&#xff1a;将一个请求封装为一个对象&#xff0c;从而可用不同的请求对客户进行参数化&#xff0c;对请求排队或者记录请求日志&#xff0c;以及支持可撤销的操作 2、命令模式结构 Command&#xff08;抽象命令类&#xff09;&#xff1a;一般是…
阅读更多...
【入门】基于DE2-115的My First FPGA 工程

【入门】基于DE2-115的My First FPGA 工程

1.1. 概述 这是一个简单的练习&#xff0c; 可以帮助初学者开始了解如何使用Intel Quartus 软件进行 FPGA 开发。 在本章节中&#xff0c;您将学习如何编译 Verilog 代码&#xff0c;进行引脚分配&#xff0c;创建时序约束&#xff0c;然后对 FPGA 进行编程&#xff0c;驱动开…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023