问题2_1

        函数$fun$的功能是：计算如下公式前 $n$项的和，并作为函数值返回。
$$S=\frac{1\times 3}{2^2}+\frac{3\times 5}{4^2}+\frac{5\times 7}{6^2}+\cdot \cdot \cdot +\frac{(2\times n-1)\times (2\times n+1)}{(2\times n{)}^2},$$
        例如，当形参$n$的值为 10 时，函数返回值为 9.612558。

代码2_1

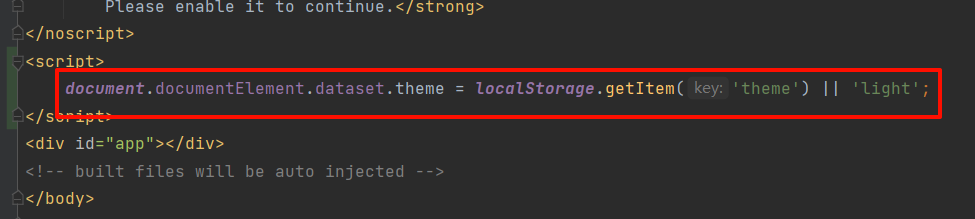
#include<stdio.h>

double fun(int n){
	int i;
	double sum, t;
	sum = 0;
	for(i=1; i<=n; i++){
		t = 2.0*i;
		sum = sum+(t-1)*(t+1)/(t*t);
	}
	return sum;
}

void main(void){
	int n = -1;
	while(n<0){
		printf("Please input(n>0):");
		scanf("%d", &n);
	}
	printf("\n The result is:%f\n", fun(n));
}

结果2_1

问题2_2

        函数$fun$的功能是：统计 $substr$ 所指的字符串在 $str$ 所指的字符串中出现的次数。
        例如，若字符串为 $aaas1kaaas$，子字符串为 $as$，函数返回值为 2。

代码2_2

#include<stdio.h>

int fun(char* str, char* substr){
	int i, j, k, num=0;
	for(i=0; str[i]; i++){
		for(j=i, k=0; substr[k]==str[j]; k++, j++){
			if(substr[k+1] == '\0'){
				num++;
				break;
			}
		}
	}
	return num;
}

void main(void){
	char str[80], substr[80];
	printf("Input a string:");
	gets(str);
	printf("Input a substring:");
	gets(substr);
	printf("%d \n", fun(str, substr));
}

结果2_2

问题2_3

        函数$fun$的功能是：根据以下公式求 $\pi$ 的值（要求精度 $0.0005$，即某项小于 $0.0005$ 时停止迭代）。
$$\frac{\pi }{2}=1+\frac{1}{3}+\frac{1\times 2}{3^5}+\frac{1\times 2\times 3}{3\times 5\times 7}+\frac{1\times 2\times 3\times 4}{3\times 5\times 7\times 9}+\cdot \cdot \cdot +\frac{(1\times 2\times ...\times n)}{(3\times 5\times ...\times (2n+1))},$$
        例如，程序运行后，若精度为 $0.0005$ ，则程序输出结果为 $3.14106$。

代码2_3

#include<stdio.h>
#include<conio.h>
#include<math.h>

double fun(double eps){
	double sum = 1.0, sum1 = 1.0;
	int n = 1;
	while(sum1 >= eps){       
		sum1 = sum1*n/(2*n+1);
		sum = sum + sum1;
		n++;
	}
	return 2*sum;
}

void main(void){
	double x;
	printf("Input eps:");
	scanf("%lf", &x);
	printf("\n eps = %lf, PI = %lf\n", x,fun(x));
}

结果2_3