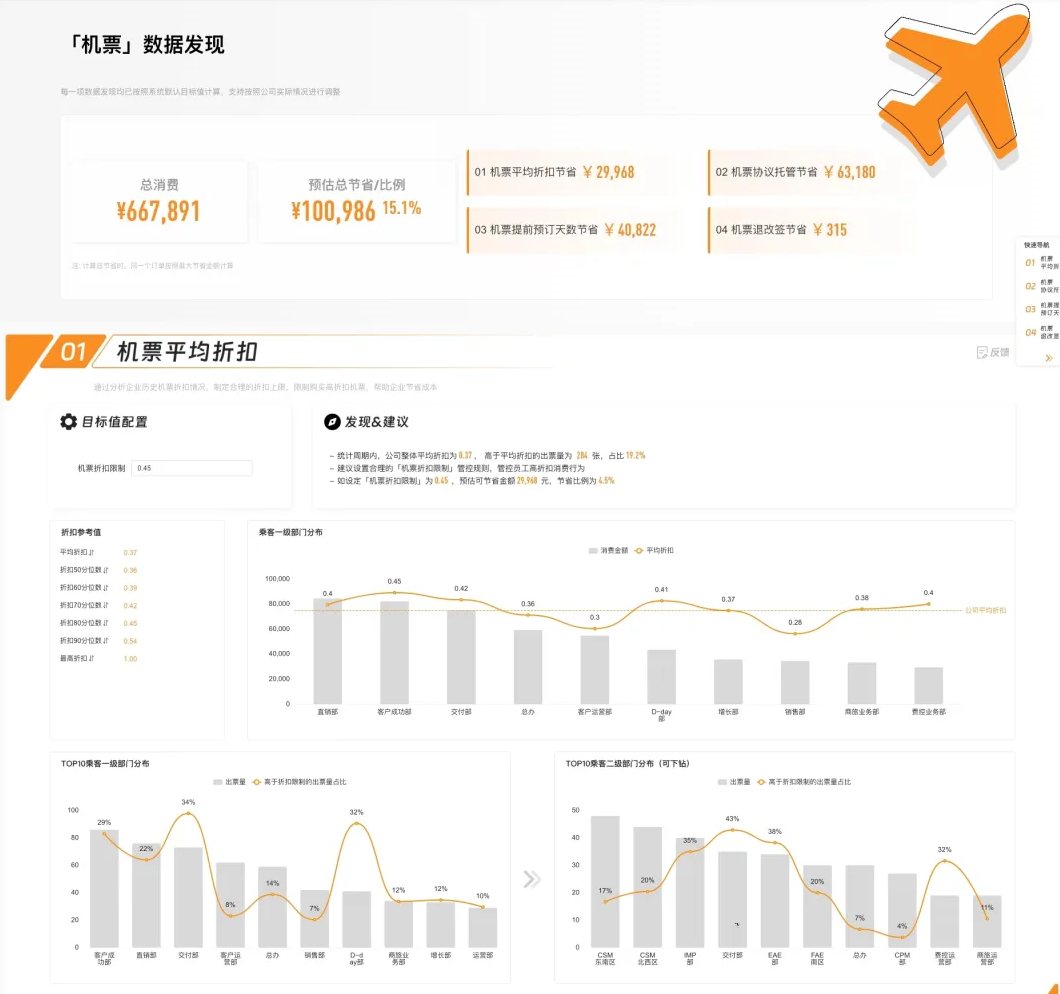
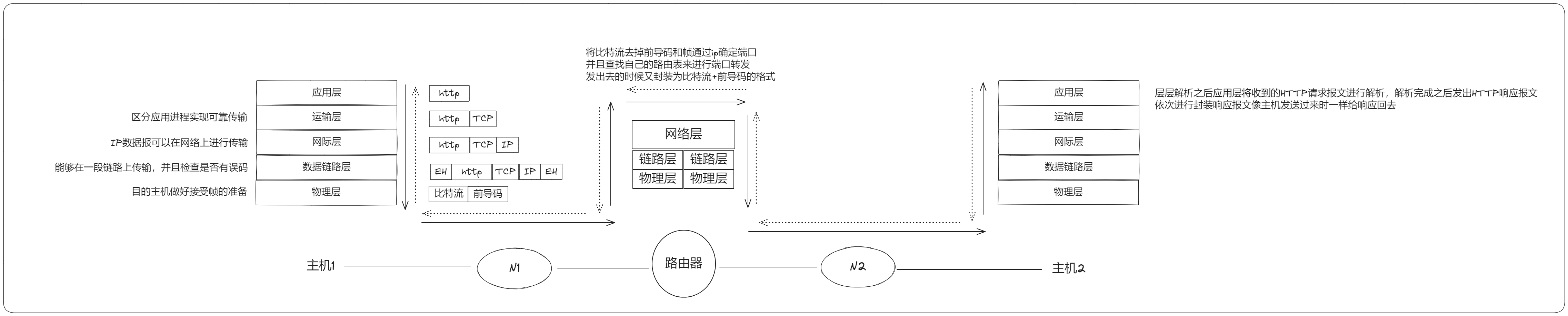
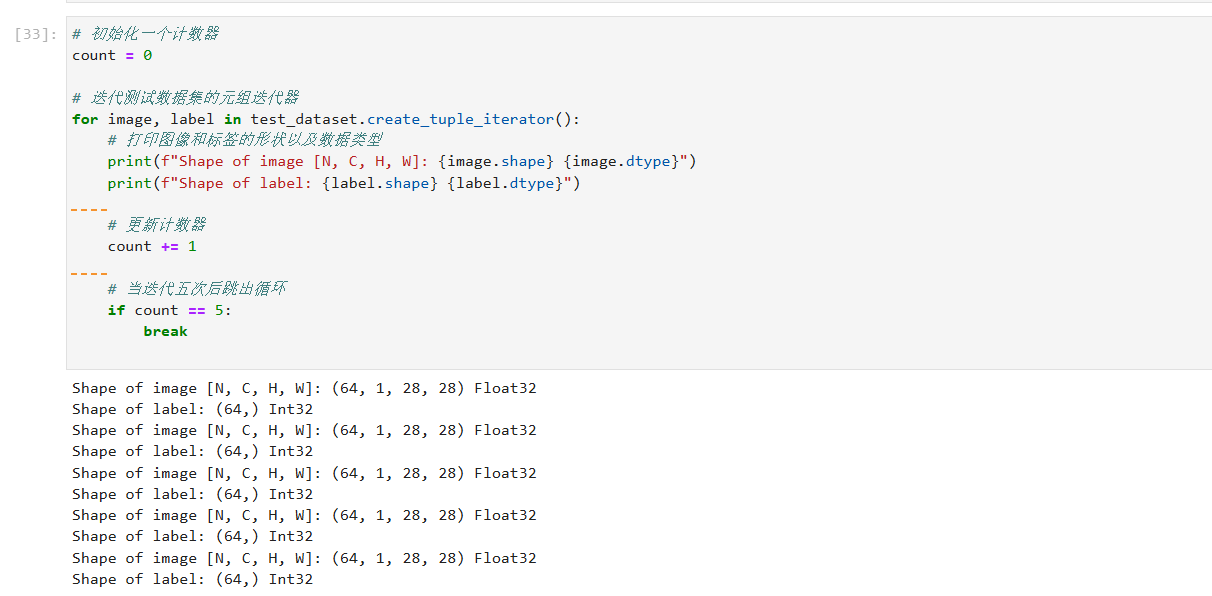
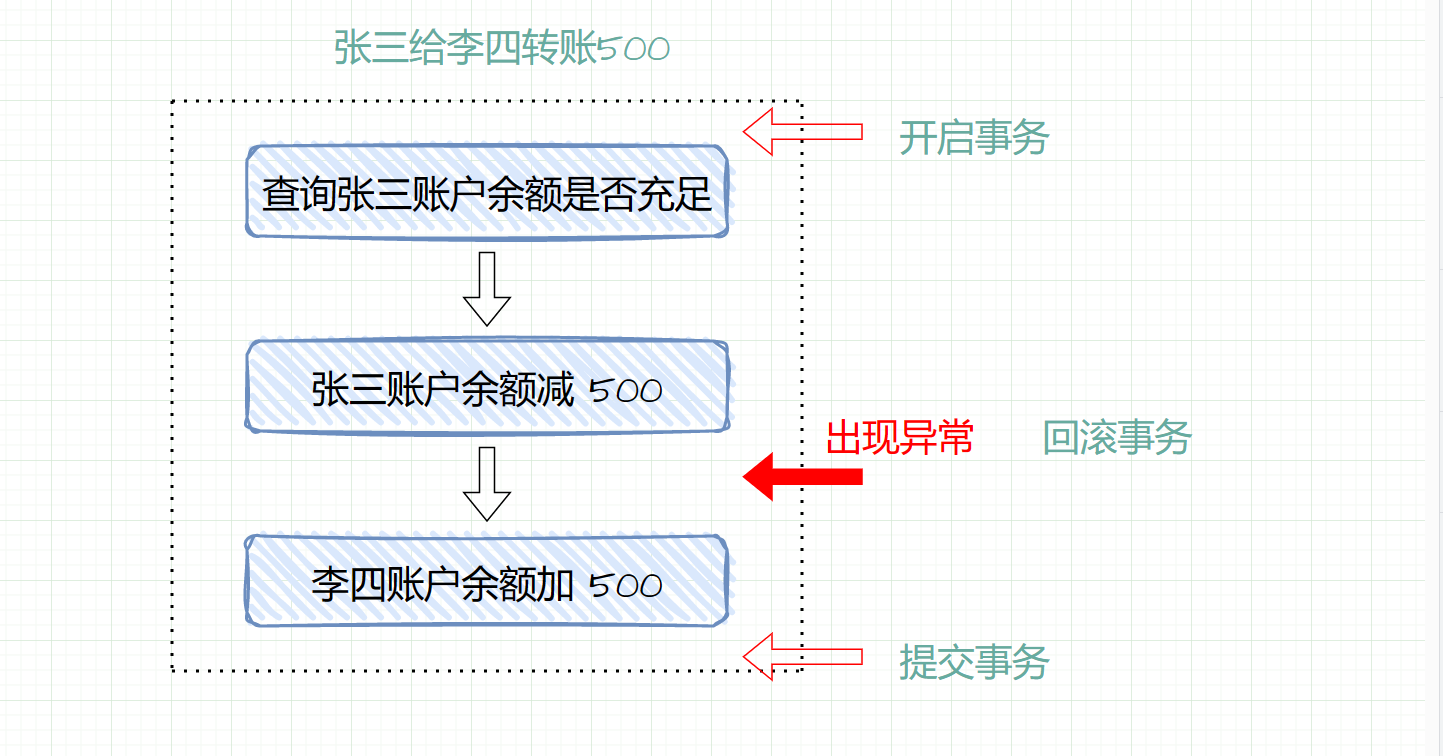
添加链接描述

题意：对于给定的n,m 。计算0~n 每一个数和m & 之后，得到的数 的二进制中 1的个数的和。

一位一位的算。最多是60位。

我们只需要计算 在 1-n这些数上，有多少个数 第i位 为1.
因为是连续的自然数，每一位上1 的出现 必然存在某种规律。
我们从 第零位 开始计数。
第 i 位 的 1 的出现周期是 2^(i+1) ，其中前一半是0，后一半是1.（数量是 2^i个）
想明白这一点之后，
对于整除的那一部分，第i位的贡献是

int w=(long long )1<<i;
n/(w*2)*w 

那么整的部分算完了，接下来算 散 的那一部分

这里可以自己找个例子，算一下。不然很同意错。
max((long long )0,n%(2*w)-w+1)

#include <bits/stdc++.h>
using namespace std;
#define int long long 
const int mod=998244353;
signed main()
{
	int n,m;cin>>n>>m;
	int ans=0;
	for (int i=0;i<60;i++)
	{
		if (m>>i &1){
			int w=(long long )1<<i;
			ans+=n/(w*2)*w+max((long long )0,n%(2*w)-w+1);
			ans%=mod;
		}
	}
	cout<<ans<<endl;
	return 0;
}