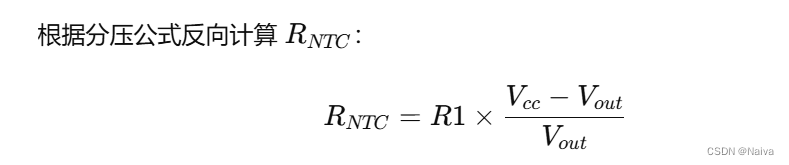目录
前言
算法原理
数学模型
Ridge 回归的估计量
Ridge 回归与标准多元线性回归的比较
3. Ridge 参数的选择
算法步骤
SPSSPRO
1、作用
2、输入输出描述
3、案例示例
4、案例数据
5、案例操作
6、输出结果分析
7、注意事项
8、模型理论
SPSSAU
岭回归分析案例
1、背景
2、理论
3、操作
4、SPSSAU 输出结果
5、文字分析
6、剖析
疑难解惑
F 值括号里面的两个值分别是什么?
智能分析每次都提示k值为0.99?
岭回归分析前是否需要对数据进行标准化处理?
岭回归时提示‘某标题数字恒定,请检查数据!’?
岭回归时没有输出标准化回归系数?
SPSSAU岭回归判断k值的标准是什么?
岭回归分析案例
其他说明
优缺点
优点
局限性
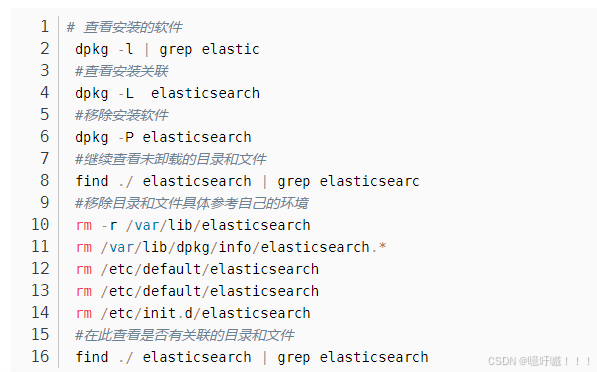
代码实现
MATLAB
R语言
python
前言
岭回归分析(Ridge Regression)是一种改良的最小二乘法,其通过放弃最小二乘法的无偏性,以损失部分信息为代价来寻找效果稍差但回归系数更符合实际情况的模型方程。
简单来说,岭回归是通过引入k个单位阵,使回归系数可以估计,得到的回归估计值要比简单线性回归系数更加稳定,也更加接近真实情况。虽然引入单位阵会导致信息丢失,但同时也换来回归模型的合理估计。
算法原理
数学模型
Ridge 回归的估计量




![[python]Markdown图片引用格式批处理桌面应用程序](python-Markdown%E5%9B%BE%E7%89%87%E5%BC%95%E7%94%A8%E6%A0%BC%E5%BC%8F%E6%89%B9%E5%A4%84%E7%90%86%E6%A1%8C%E9%9D%A2%E5%BA%94%E7%94%A8%E7%A8%8B%E5%BA%8F/image-20240706075502201.png)