【论文通读】RuleR: Improving LLM Controllability by Rule-based Data Recycling

news2025/11/4 17:53:02

RuleR: Improving LLM Controllability by Rule-based Data Recycling

前言
Abstract
Motivation
Solution
Method
Experiments
Conclusion

前言

一篇关于提升LLMs输出可控性的短文，对SFT数据以规则的方式进行增强，从而提升SFT数据的质量，进而间接帮助提升LLM的可控性。这种基于规则的方式确实可以去除人力和额外的LLM资源的开销，但是在某种程度上可能不能真正泛化到具体的数据上。

Paper	https://arxiv.org/abs/2406.15938
Code	https://github.com/MingLiiii/RuleR

Abstract

LLMs缺乏稳定可控的输出，这对产品表现和用户体验不利。然而现有的用于提升LLMs可控性的SFT数据集经常依赖人类经验或者大模型，需要付出额外的成本。相比于从头构建新数据集，RuleR对现有的数据集进行重新利用，对其输出注入基于规则的编辑，并将基于规则的指令append到原始的指令中。实验表明RuleR可以高效提升LLM的可控性，同时不降低模型通用性能。

Motivation

当前如何最大化利用LLMs的能力是一个重要问题，其关键在于让LLMs的输出遵循用户的要求。但是如果对输出没有约束，生成的结果很难有实际效用。

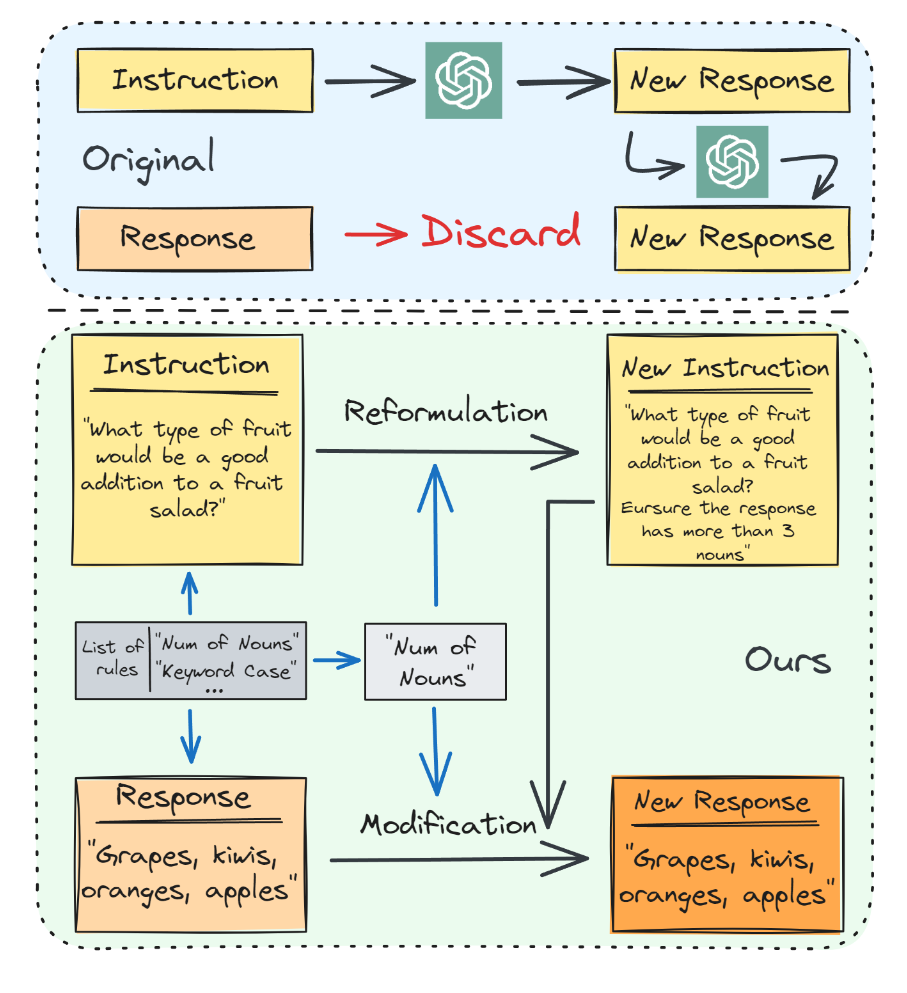
然而现有的方法通过构建SFT数据集，但是这种方法只能关注到通用的指令，忽略了用户特定的约束。一个可行的解决方法是通过模型或者人类改写指令，但成本高。
能不能通过重新利用现有SFT数据集，在不采用人力和模型的情况下，为其赋予不同类型的约束，从而进行可控微调？

Solution

本文提出Rule-based Data Recycling (RuleR)，可以自动化编辑现有的SFT数据，用于提升LLM的可控性。其核心是利用各种预定义的约束规则来代替人力和模型。预定义的规则cover广泛的约束，从high-level到lower-level。对于每个规则，包括：

一组约束模板。
交替编辑指令和Response以以使他们align。

上图的下面部分是一个例子。

Method

在没有人类或者LLM引导的情况下，直接添加任意约束到原始的指令中是不合适的。为此，本文提出只添加和原始数据吻合的约束。具体来说，作者提出基于规则的RuleR方法来增强LLM的可控性，其中用于重新制定的规则和约束由原始数据来确定，确保指令和响应之间的一致性。下表是完整的规则列表：

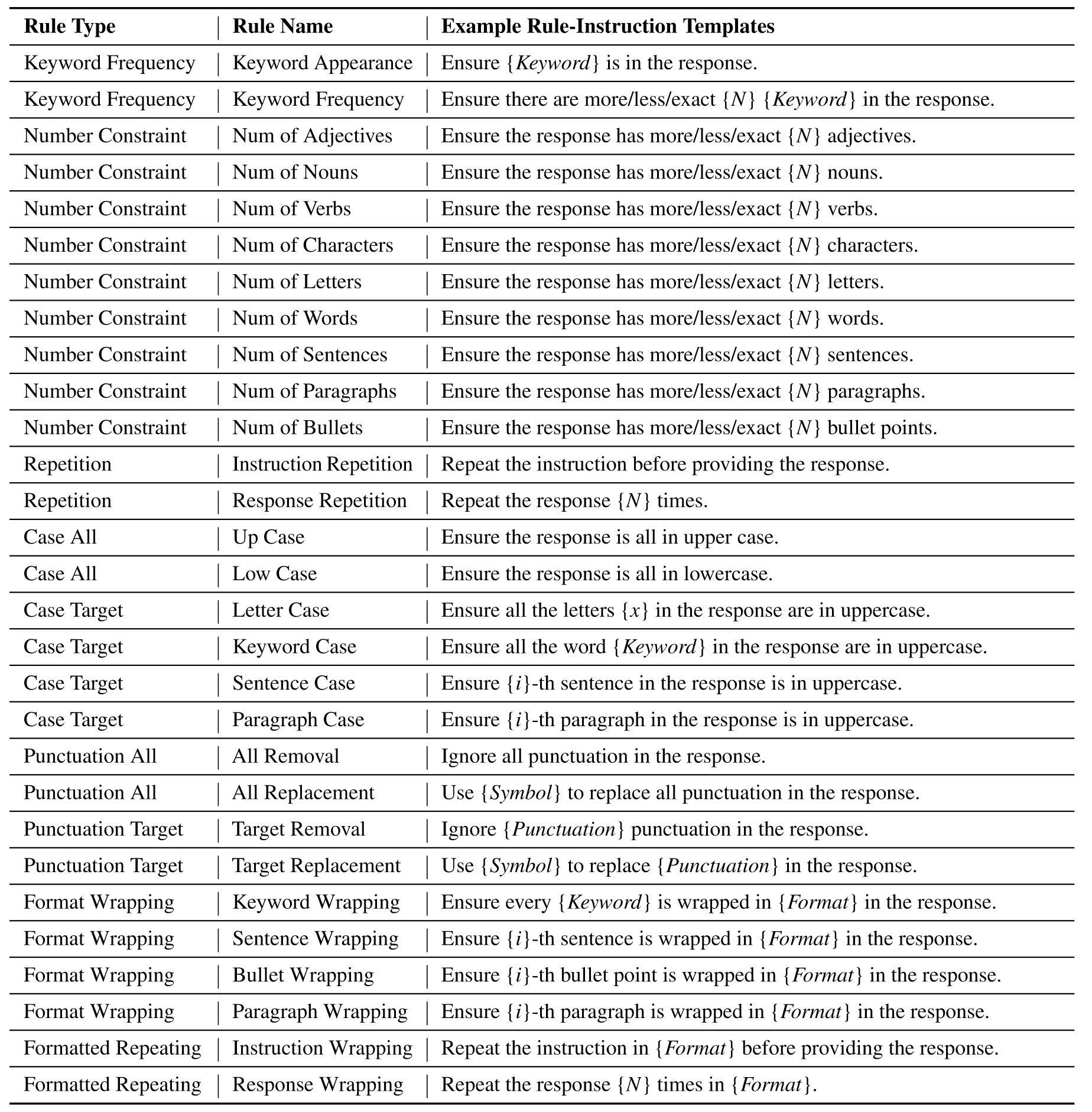
在方法实施时，作者将每个预定义的规则实例化为一个元组：
$(\mathbf{S} _k,f_k,g_k)$
其中 $\mathbf{S} _k$ 表示第k条规则对应的指令模板集， $f _k$ 和 $g_k$ 分别表示重构指令的函数和可选修改response的函数。对于样本 $x_i,y_i)$ ，增强指令会由如下公式获取：
$x_{i, a u g}=f_{k}\left(x_{i}, y_{i}, \mathbf{S}_{k}\right)$
具体来说，随机抽取一个规则指令模板，并填充相应的特征，作为对原始指令的附加约束。然后，规则指令与原始指令连接成为增强指令。对于标签y，也可以类似的选择性修改：
$y_{i, a u g}=g_{k}\left(x_{i}, y_{i}, \mathbf{S}_{k}\right)$
对于某些规则，无需对response进行修改。

Experiments

作者在一系列开源模型和开源SFT数据集上进行实验，实验结果如下：

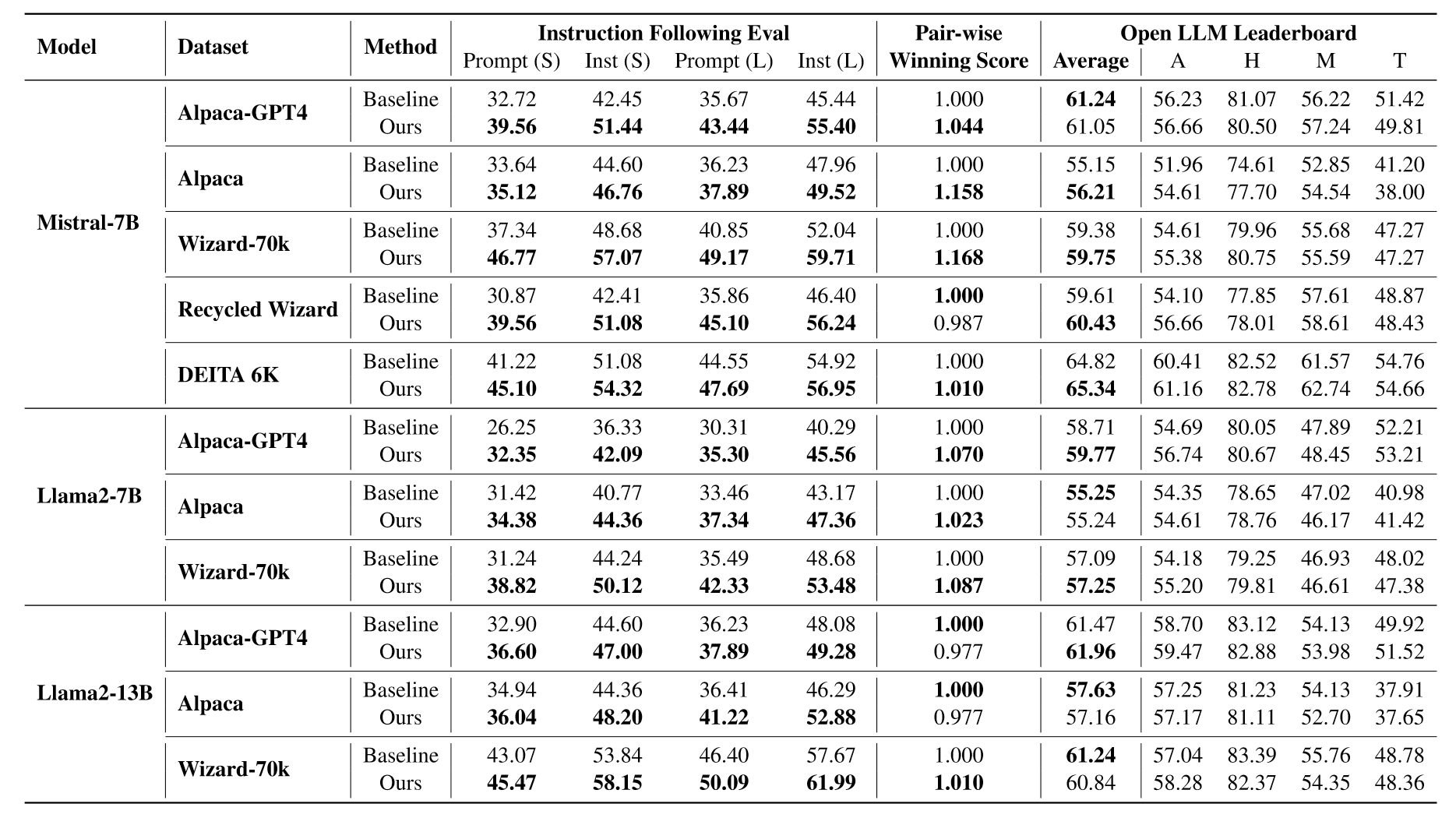
结果显著，一些数据集上提点能够达到10%。
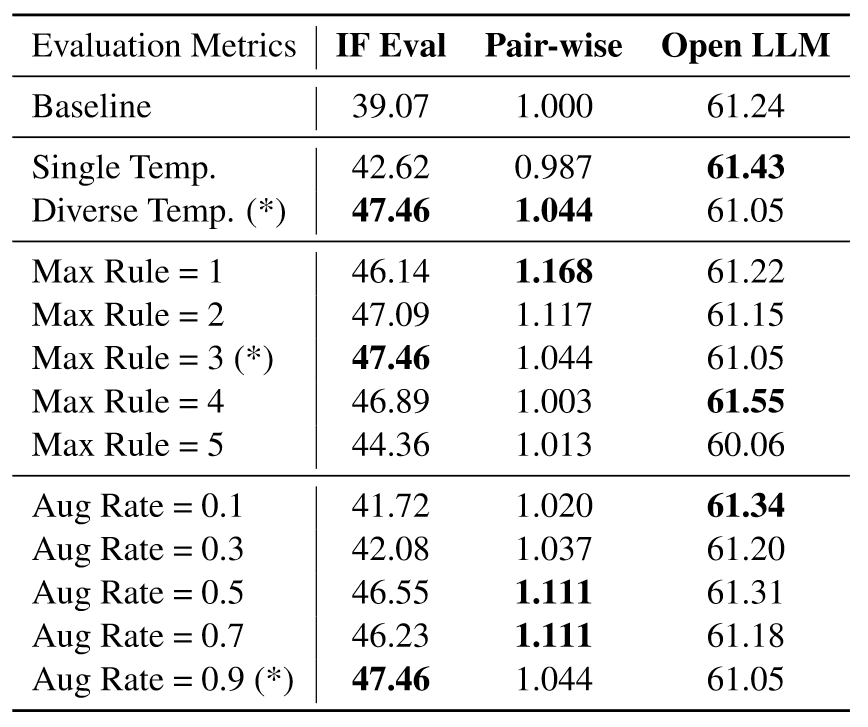
下表是消融实验结果。Single Temp意味一个规则使用一个模板，Diverse Temp意味一个规则对应多个模板，Max Rule 表示每个原始数据样本上最多可以采样和利用x个不同规则的设置。结果显示在一个样本中使用太多的规则可能会损害模型的性能。Aug Rate指的是将增强应用于每个样本的概率，可以看到，随着Aug Rate的增加，LLM可控性越好，但是对一般指令的跟踪能力有所下降。IF Eval的变化大，说明方法主要还是和可控性有关。

Conclusion

本文提出一个新颖的方法，即基于规则的数据回收方法RuleR，它利用从现有数据派生的约束来增强数据集，并将这些约束纳入训练过程，从而提高LLM的多约束可控性。这种方法为开发 SFT 增强方法以提高 LLM 的可控性提供了一个有前途的方向，为 LLM 更有效的进步铺平了道路。
这篇工作简单易懂，且效果显著，但是我也有一些额外的想法：

方法中提到“we propose to only incorporate constraints that are compatible with the original data sample.”但是注入规则时却是随机抽取一个规则指令模板，我很难将随机采样和“compatible with the original data sample”理解到一起。
基于规则的增强过程在文章中的描述过于泛泛，具体来说， $f _k$ 和 $g_k$ 这两个函数具体是怎么执行的没有详细说明，导致不是很好理解，也许对于这两个函数举出特定的一两个例子会更好。
基于规则的方法真的可以泛化到每一个特定的样本上吗，我不是很能确定。
图一中作者方法部分列举的例子让我感到困惑，Response和New Response内容一样，虽然文中提到remains unchanged，但是这个例子显然不能说明Modification的作用。