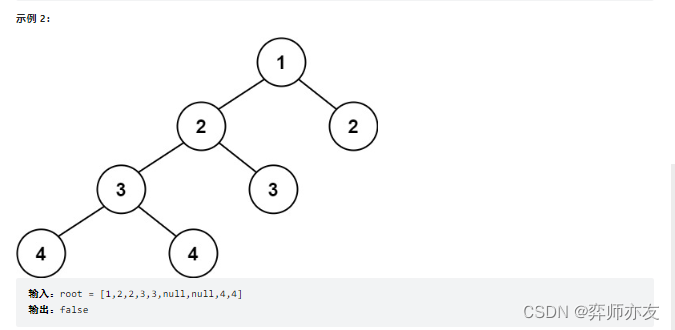
110.平衡二叉树

看完题后的思路

1. int[] f(root)
2. if root=null return [true,0]
3. left[]=f(root.left)
   if(!left[0]){return [false,-1]}
   right[]=f(root.right)
   if(!right[0]){return [false,-1]}
   return[true,math.max(left[1],right[1])+1]

思路

上面的过程弄复杂了，其实直接返回高度即可，如果子树是平衡二叉树，返回树的高度，如果不是，返回-1.

代码

 // 110. 平衡二叉树
        public boolean isBalanced(TreeNode root) {
            Object[] objects = isBalanced02(root);
            return (Boolean) objects[0];
        }
        public Object[] isBalanced02(TreeNode root) {
            if (root==null){
                return new Object[]{true,0};
            }
            Object[] left = isBalanced02(root.left);
            if (!(Boolean) left[0]){
                return new Object[]{false,0};
            }
            Object[] right = isBalanced02(root.right);
            if (!(Boolean)right[0]){
                return new Object[]{false,0};
            }
              Integer leftHeight = (Integer) left[1];
            Integer rightHeight = (Integer) right[1];
            if (Math.abs(leftHeight-rightHeight)<=1){
                return new Object[]{true,Math.max((Integer)left[1],(Integer) right[1])+1};
            }else {
                return new Object[]{false,-1};
            }
        }

复杂度

收获

本题回溯做法可以大框架使用后续迭代，然后求每个节点的高度，效率很低
三刷大脑过一遍

257. 二叉树的所有路径

看完题后的思路

本题本质是回溯算法

1. 递归参数
   是指一个全局变量
   void f（root，Stringbuild path）
2. 终止条件
   if root==nul 将处理后的path加入list，return
3. 递归
   终止判断
   path.add(root)
   f（root.left,path）;
   f(root.right,payh);
   // 回溯
   path.remove（root）
   错误，看代码

代码

 ArrayList<String> binaryTreePathsRes = new ArrayList<>();
        public List<String> binaryTreePaths(TreeNode root) {
        
            binaryTreePathsBT(root,new StringBuilder());
            return binaryTreePathsRes;
        }
    public void binaryTreePathsBT(TreeNode root,StringBuilder sb) {
        sb.append(root.val);
        sb.append("->");
        if (root.left==null&&root.right==null){
            //sb.delete(sb.length()-1,sb.length());
            //binaryTreePathsRes.add(sb.toString());
             String string = sb.toString();
            
            binaryTreePathsRes.add(string);
            return;
        }
      
       if (root.left!=null){
            binaryTreePathsBT(root.left,sb);
            sb.delete(sb.length()-3,sb.length());
        }
       
        if (root.right!=null){
            binaryTreePathsBT(root.right,sb);
            sb.delete(sb.length()-3,sb.length());
        }
    }

代码有点小问题，使用sb删除的时候是按字符删，引文数字位数不同，所以不知道删除几个

收获

当终止条件是叶子节点的时候，需要首先加入叶子节点
每次执行完都要回溯，删除的是子节点，不是自己，最终这种模式最终会剩下根节点
三刷敲一遍

404.左叶子之和

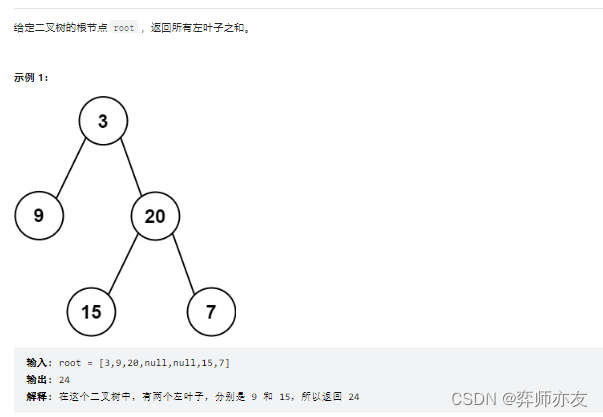
看完题后的思路

使用前序遍历

 int sumOfLeftLeavesRes=0;
      public void sumofleftleaves(TreeNode root,TreeNode pre) {
        if (root==null){
            return;
        }
        if (root.left==null&&root.right==null&&pre.left==root){
            sumOfLeftLeavesRes+=root.val;
        }
        sumofleftleaves(root.left,root);
        sumofleftleaves(root.right,root);

    }
    public int sumOfLeftLeaves(TreeNode root) {
        // 特殊条件判断
          if (root==null||(root.left==null&&root.right==null)){
            return 0;
        }
        // TreeNode iroot = new TreeNode();
        // iroot.left=root;
        sumofleftleaves(root,null);
        return sumOfLeftLeavesRes;
    }

复杂度

收获

本题有前序前一个节点代码
本题三刷要看一遍
本题后续也可以，三刷再来看