数据结构之二叉树
- 二叉树
- 简介
- 分类
- 普通二叉树
- 平衡二叉树
- 满二叉树
- 二叉搜索树(二叉排序树、二叉查找树),
- 平衡二叉树
- 红黑树
- B树类型
- B树(B-树、B_树)
- B+树
- B*树
二叉树
简介
二叉树(Binary Tree) :是一种非常重要的非线性结构。:二叉树是每个节点最多有两个子树的树结构;
是n(n>=0)个结点的有限集合,它或者是空树(n=0),或者是由一个根结点及两颗互不相交的、分别称为左子树和右子树的二叉树所组成
节点:Node, 二叉树是由N个节点组成,(每个节点有两个子节点的指针(也可以没有),分别为左子节点,右子节点)。
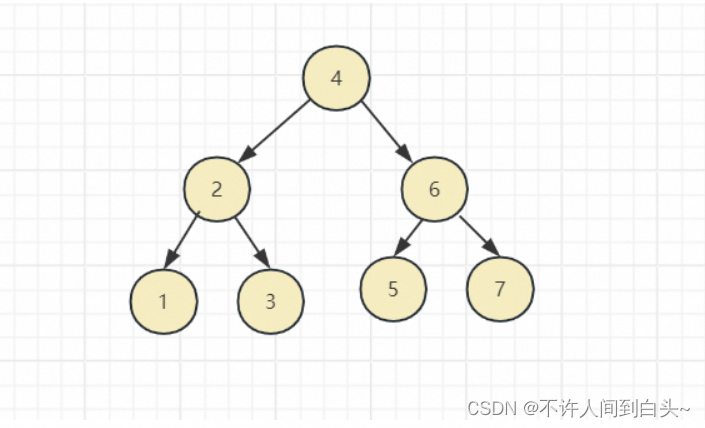
根节点:没有父节点的节点就是根节点(唯一),也就是第一层的哪一个节点。如图所示:4
叶子节点:没有子节点的节点就是叶子节点。如图所示:1,3,5,7
非叶子节点:有子节点的节点就是非叶子节点。如图所示:2,6,4(4 是根节点也是特殊的非叶子节点)
度:表示节点的子节点个数,因为子节点最大数量为2 (左子,右子),所以度最大为2.
高度:也称树的深度(层高)等,表示树的层级。如图所示:树高度为3.
每层节点数量:N = 2^(h-1) . N(每层数量),h (层级)。
树总节点数量:N = (2^h) - 1. N(每层数量),h (层级)。
如图所示
分类
二叉树也有类别:
普通二叉树
平衡二叉树
除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少右边的若干结点
- 叶子结点只能出现在最下层和次下层。
- 最下层的叶子结点集中在树的左部。
- 倒数第二层若存在叶子结点,一定在右部连续位置。
- 如果结点度为1,则该结点只有左孩子,即没有右子树。
- 同样结点数目的二叉树,完全二叉树深度最小
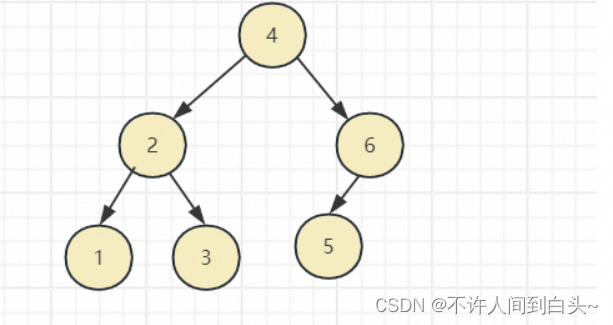
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树
- 叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
- 非叶子结点的度(
结点拥有的子树数目称为结点的度)一定是2 - 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多
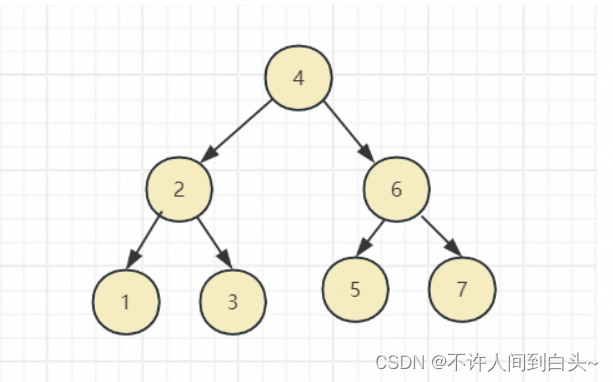
二叉搜索树(二叉排序树、二叉查找树),
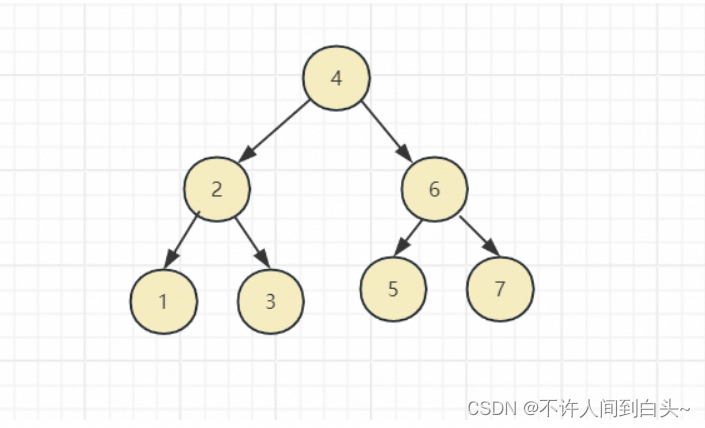
二叉排序树:可以为空树,或者是具备如下性质:若它的左子树不空,则左子树上的所有结点的值均小于根节点的值;若它的右子树不空,则右子树上的所有结点的值均大于根节点的值,左右子树分别为二叉排序树。
如下图所示
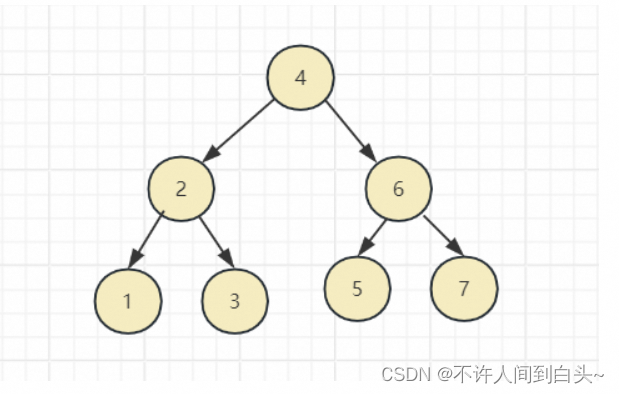
平衡二叉树
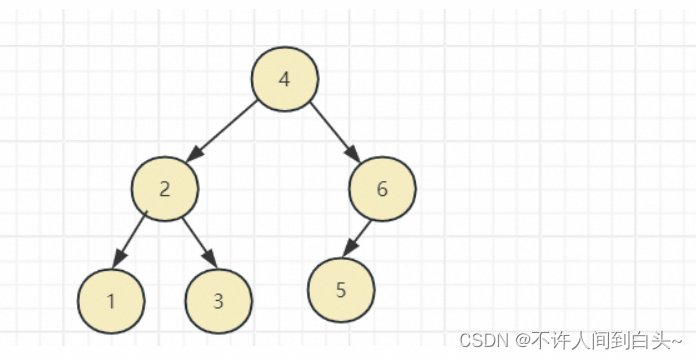
平衡二叉树是一种概念,是二叉查找树的一个进化体,它有几种实现方式:红黑树、AVL树
它是一个空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是平衡二叉树,如果插入或者删除一个节点使得高度之差大于1,就要进行节点之间的旋转,将二叉树重新维持在一个平衡状态。
这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多
AVL实现平衡的关键在于旋转操作:
插入和删除可能破坏二叉树的平衡,此时需要通过一次或多次树旋转来重新平衡这个树。
当插入数据时,最多只需要1次旋转(单旋转或双旋转);但是当删除数据时,会导致树失衡,AVL需要维护从被删除节点到根节点这条路径上所有节点的平衡,旋转的量级为O(lgn)
由于旋转的耗时,AVL树在删除数据时效率很低;在删除操作较多时,维护平衡所需的代价可能高于其带来的好处,因此AVL实际使用并不广泛
红黑树
红黑树是一种平衡二叉查找树的变体,它的左右子树高差有可能大于1,所以红黑树不是严格意义上的平衡二叉树(AVL),但对之进行平衡的代价较低, 其平均统计性能要强于 AVL
- 每个节点或者是黑色,或者是红色
- 根节点是黑色
- 每个叶结点是黑色
- 如果一个节点是红色的,则它的子节点必须是黑色的,红色节点的孩子和父亲都不能是红色。从每个叶子到根的所有路径上不能有两个连续的红色节点,任意一结点到每个叶子结点的路径都包含数量相同的黑结点。确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对接近平衡的二叉树,并不是一个完美平衡二叉查找树
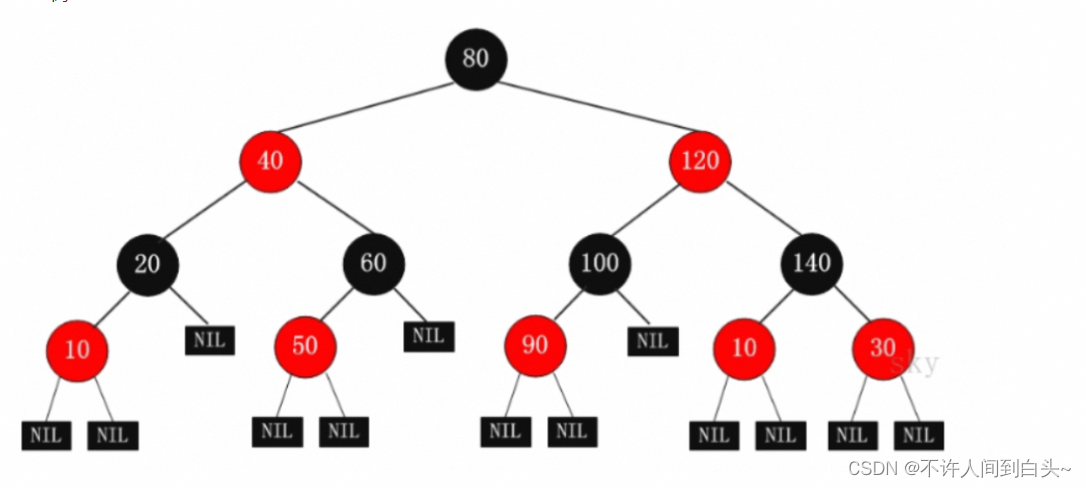
红黑树和AVL树区别
RB-Tree和AVL树作为二叉搜索树(BBST),其实现的算法时间复杂度相同,AVL作为最先提出的BBST,貌似RB-tree实现的功能都可以用AVL树是代替,那么为什么还需要引入RB-Tree呢
- 红黑树不追求
完全平衡,即不像AVL那样要求节点的高度差的绝对值<= 1,它只要求部分达到平衡,但是提出了为节点增加颜色,红黑是用非严格的平衡来换取增删节点时候旋转次数的降低,任何不平衡都会在三次旋转之内解决,而AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多 - 就插入节点导致树失衡的情况,
AVL和RB-Tree都是最多两次树旋转来实现复衡rebalance,旋转的量级是O(1) - 删除节点导致失衡,
AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡,旋转的量级为O(logN),而RB-Tree最多只需要旋转3次实现复衡,只需O(1),所以说RB-Tree删除节点的rebalance的效率更高,开销更小 AVL的结构相较于RB-Tree更为平衡,插入和删除引起失衡,RB-Tree复衡效率更高;当然,由于AVL高度平衡,因此AVL的Search效率更高- 针对插入和删除节点导致失衡后的
rebalance操作,红黑树能够提供一个比较便宜的解决方案,降低开销,是对search,insert,以及delete效率的折衷,总体来说,RB-Tree的统计性能高于AVL - 故引入
RB-Tree是功能、性能、空间开销的折中结果
AVL更平衡,结构上更加直观,时间效能针对读取而言更高;维护稍慢,空间开销较大。
红黑树,读取略逊于AVL,维护强于AVL,空间开销与AVL类似,内容极多时略优于AVL,维护优于AVL。
缺点:对于数据在内存中的情况,红黑树的表现是非常优异的。但是对于数据在磁盘等辅助存储设备中的情况(如MySQL等数据库),红黑树并不擅长,因为红黑树长得还是太高了。当数据在磁盘中时,磁盘IO会成为最大的性能瓶颈,设计的目标应该是尽量减少IO次数;而树的高度越高,增删改查所需要的IO次数也越多,会严重影响性能
总结:实际应用中,若搜索的次数远远大于插入和删除,那么选择AVL,如果搜索,插入删除次数几乎差不多,应该选择RB-Tree
B树类型
B树(B-树、B_树)
一种平衡的多叉树,称为B树(或B-树、B_树,B:balanced说明B树和平衡树有关系)
B树是为磁盘等辅存设备设计的多路平衡查找树,与二叉树相比,B树的每个非叶节点可以有多个子树。 因此,当总节点数量相同时,B树的高度远远小于AVL树和红黑树(B树是一颗“矮胖子”),磁盘IO次数大大减少。
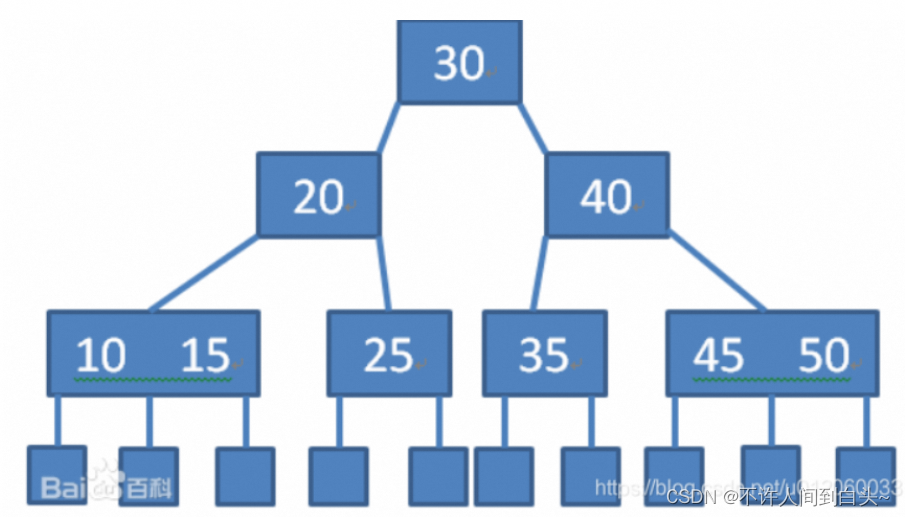
一棵M阶B树(M阶数:表示此树的结点最多有多少个孩子结点(子树))是一棵平衡的m路搜索树。它或者是空树,或者是满足下列性质的树:
- 每个节点最多包含 m 个子节点
- 根结点至少有两个子节点,除根节点外,每个非叶节点至少包含 m/2 个子节点;
- 拥有 k 个子节点的非叶节点将包含 k - 1 条记录
- 每个非根节点所包含的关键字个数 j 满足:┌m/2┐ - 1 <= j <= m - 1;
- 除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足:┌m/2┐ <= k <= m ;
- 所有的叶子结点都位于同一层。
简单理解为:平衡多叉树为B树(每一个子节点上都是有数据的),叶子节点之间无指针相邻
B树的搜索,从根结点开始,如果查询的关键字与结点的关键字相等,那么就命中;否则,如果查询关键字比结点关键字小,就进入左儿子;如果比结点关键字大,就进入右儿子;如果左儿子或右儿子的指针为空,则报告找不到相应的关键字;重复,直到所对应的儿子指针为空,或已经是叶子结点
如果B树的所有非叶子结点的左右子树的结点数目均保持差不多(平衡),那么B树的搜索性能逼近二分查找;但它比连续内存空间的二分查找的优点是,改变B树结构(插入与删除结点)不需要移动大段的内存数据,甚至通常是常数开销;但B树在经过多次插入与删除后,有可能导致不同的结构
B-树的特性:
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
- 自动层次控制;
由于M阶B树每个结点最少M/2个结点的限制,是为了最大限度的减少查找路径的长度,提供查找效率
B树在数据库中有一些应用,如mongodb的索引使用了B树结构。但是在很多数据库应用中,使用了是B树的变种B+树
B+树
B+树是B树的一种变形形式,B+树上的叶子结点存储关键字以及相应记录的地址,叶子结点以上各层作为索引使用。一棵m阶的B+树定义如下
- 每个结点至多有m个子女;
- 除根结点外,每个结点至少有[m/2]个子女,根结点至少有两个子女;
- 有k个子女的结点必有k个关键字
B+树的查找与B树不同,当索引部分某个结点的关键字与所查的关键字相等时,并不停止查找,应继续沿着这个关键字左边的指针向下,一直查到该关键字所在的叶子结点为止。
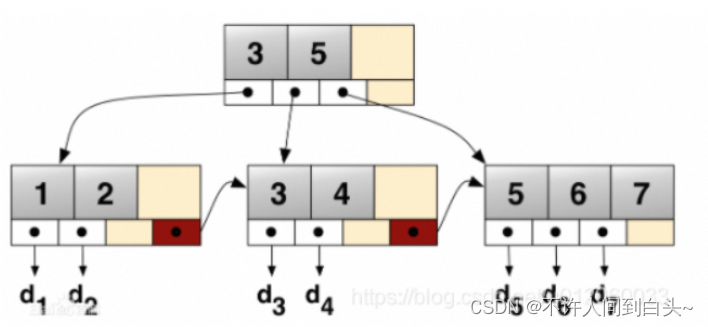
B+树也是多路平衡查找树,其与B树的区别主要在于:
B树中每个节点(包括叶节点和非叶节点)都存储真实的数据,B+树中只有叶子节点存储真实的数据,非叶节点只存储键。
在MySQL中,这里所说的真实数据,可能是行的全部数据(如Innodb的聚簇索引),也可能只是行的主键(如Innodb的辅助索引),或者是行所在的地址(如MyIsam的非聚簇索引)
点击了解MySQL中索引数据结构分析B树中一条记录只会出现一次,不会重复出现,而B+树的键则可能重复重现——一定会在叶节点出现,也可能在非叶节点重复出现。B+树的叶节点之间通过双向链表链接B树中的非叶节点,记录数比子节点个数少1;而B+树中记录数与子节点个数相同。
由此,B+树与B树相比,有以下优势:
- 更少的
IO次数:B+树的非叶节点只包含键,而不包含真实数据,因此每个节点存储的记录个数比B树多很多(即阶m更大),因此B+树的高度更低,访问时所需要的IO次数更少。此外,由于每个节点存储的记录数更多,所以对访问局部性原理的利用更好,缓存命中率更高。 - 更适于范围查询:在
B树中进行范围查询时,首先找到要查找的下限,然后对B树进行中序遍历,直到找到查找的上限;而B+树的范围查询,只需要对链表进行遍历即可。 - 更稳定的查询效率:
B树的查询时间复杂度在1到树高之间(分别对应记录在根节点和叶节点),而B+树的查询复杂度则稳定为树高,因为所有数据都在叶节点。
B+树也存在劣势:由于键会重复出现,因此会占用更多的空间。但是与带来的性能优势相比,空间劣势往往可以接受,因此B+树的在数据库中的使用比B树更加广泛。
B*树
B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;所以,B*树分配新结点的概率比B+树要低,空间使用率更高
B树类型总结:
二叉搜索树:二叉树,每个结点只存储一个关键字,等于则命中,小于走左结点,大于走右结点;B树(B-树):多路搜索树,每个结点存储M/2到M(M是指M阶B树)个关键字,非叶子结点存储指向关键字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;B+树:在B-树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3