【题目来源】
https://www.acwing.com/problem/content/1258/
【题目描述】
由于先序、中序和后序序列中的任一个都不能唯一确定一棵二叉树,所以对二叉树做如下处理,将二叉树的空结点用 · 补齐,如图所示。
我们把这样处理后的二叉树称为原二叉树的扩展二叉树,扩展二叉树的先序或后序序列均能唯一确定其二叉树。
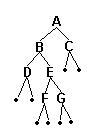
现给出扩展二叉树的先序序列,要求输出原二叉树中序和后序序列。
【输入格式】
扩展二叉树的先序序列。
【输出格式】
输出其中序和后序序列。
【数据范围】
原二叉树的结点数不超过 26,且均由大写字母表示。
【输入样例】
ABD..EF..G..C..
【输出样例】
DBFEGAC
DFGEBCA
【算法分析】
扩展二叉树的前序遍历相当于普通二叉树的“前序+中序”,能唯一确定二叉树的形状;
扩展二叉树的后序遍历相当于普通二叉树的“后续+中序”,能唯一确定二叉树的形状。
【算法代码】
#include <bits/stdc++.h>
using namespace std;
string pre;
string in,post;
int k;
void dfs() {
char root=pre[k++];
if(root=='.') return;
dfs(); //Enter the left subtree
in+=root;
dfs(); //Enter the right subtree
post+=root;
}
int main() {
cin>>pre;
dfs();
cout<<in<<endl;
cout<<post<<endl;
return 0;
}
/*
in:
ABD..EF..G..C..
out:
DBFEGAC
DFGEBCA
*/
【参考文献】
https://www.cnblogs.com/0fflineboy/p/15403913.html
https://www.acwing.com/solution/content/36138/
https://blog.csdn.net/m0_72895175/article/details/132356141