机械原理介绍
- 1 介绍
- 1.1 概述
- 1.2 资料
- 书籍
- 在线资料
- 2 [机械原理知识整理](https://tomm.muzing.top/) 【muzing整理编写】
- 1 绪论
- 2 机构的结构分析
- 2-2 机构的组成及分类
- 2-3 机构运动简图
- 2-4 机构具有确定运动的条件及最小阻力定律
- 2-5 2-6 机构自由度的计算
- 2-7 平面机构的组成原理、结构分类及结构分析
- 3 平面机构的运动分析
- 3-2 用图解法作机构的运动分析
- 4 平面机构的力分析
- 4-1 机构力分析
- 4-3运动副中摩擦力的确定
- 5 机械的效率和自锁
- 5-1 机械的效率
- 5-2 机械的自锁
- 6 机械的平衡
- 6-1 机械平衡的目的及内容
- 6-2 刚性转子的平衡计算
- 6-3 刚性转子的平衡实验
- 6-4 转子的许用不平衡量和许用不平衡度
- 6-5 平面机构的平衡
- 7 机械的运转及其速度波动的调节
- 7-1 概述
- 7-4 稳定运转状态下机械的周期性速度波动及其调节
- 8 连杆机构及其设计
- 8-1 连杆机构及其传动特点
- 8-2 平面四杆机构的类型及应用
- 8-3 平面四杆机构的基本知识
- 8-4平面四杆机构的设计
- 9 凸轮机构及其设计
- 9-1 凸轮机构的应用及分类
- 9-2 推杆的运动规律
- 推杆运动规律:
- 刚性冲击
- 柔性冲击
- 多项式运动规律
- 三角函数运动规律
- 9-3 凸轮轮廓曲线的设计
- 理论廓线(cam pitch curve)
- 实际廓线(cam contour)
- 9-4 凸轮机构基本尺寸的确定
- 压力角
- 基圆半径的确定
- 变尖与失真
- 10 齿轮机构及其设计
- 10-1 齿轮机构的特点及类型
- 优点:
- 缺点:
- 用于平行轴间传动的齿轮机构
- 用于相交轴间传动的齿轮机构
- 用于交错轴间传动的齿轮机构
- 10-2 齿轮的齿廓曲线
- 10-3 渐开线齿廓及其啮合特点
- 渐开线方程式:
- 10-4 渐开线标准齿轮的基本参数和几何尺寸
- 齿轮各部分的名称和符号:
- 渐开线齿轮的基本参数:
- 10-5 渐开线直齿圆柱齿轮的啮合传动
- 10-6 渐开线齿廓的切制原理与根切现象
- 10-7 渐开线变位齿轮简介
- 10-8 斜齿圆柱齿轮传动
- 10-9 直齿锥齿轮传动
- 10-10 蜗轮蜗杆传动
- 蜗轮蜗杆正确啮合的条件:(阿基米德蜗轮蜗杆)
- 11 齿轮系及其设计
- 11-1 齿轮系及其分类
- 11-2 定轴轮系的传动比
- 11-3 周转轮系的传动比
- 11-4 复合轮系的传动比
- 11-5 轮系的功用
- 12 其他机构
- 12-1 棘轮机构
- 12-2槽轮机构
- 12-4 凸轮式间歇运动机构
- 12-5 不完全齿轮机构
- 参考
1 介绍
1.1 概述
机械(machinery)是机器(machine)和机构(mechanism)的总称。
一般简单的叫机构,复杂的叫机器。

1.2 资料
书籍
- 《机械原理》[第八版] 孙恒、陈作模、葛文杰主编(西北工业大学 机械原理及机械零件教研室)
- 《机械原理》[第七版] 郑文伟
- Monograph-on-Theory-of-Machine-Raman-Gahlaut
- Theory of Machines and Mechanisms
在线资料
- 机械原理知识整理
2 机械原理知识整理 【muzing整理编写】
如下由 muzing 编写,本人整理只为了搜索内容方便
详见
- 主页:https://muzing.top/
- 整理:https://tomm.muzing.top/

1 绪论
机械(machinery)是机器(machine)和机构(mechanism)的总称。
机构:
用来传递与变换运动和力的可动的装置
机器:
根据某种使用要求而设计的用来变换或传递能量、物料和信息的执行机械运动的装置
本书研究的内容主要包括以下几个方面:
- (1)机构结构分析的基本知识
-
- 机构的组成、机构具有确定运动的条件
-
- 机构的组成原理及机构的结构分类
-
- 绘制机构运动简图
- (2)机构的运动分析
- (3)机器动力学
-
- 分析机器在运转过程中其各构件的受力情况以及这些力的作功情况
-
- 研究机器在已知外力作用下的运动、机器速度波动的调节、不平衡惯性力的平衡问题
- (4)常用机构的分析与设计
- (5)机械系统的方案设计
2 机构的结构分析
2-2 机构的组成及分类
构件(link)
机器中每一个独立的运动单元体称为一个构件
运动副(kinematic pair)
- 由两个构件直接接触而组成的可动的连接
- 运动副元素:上述两构件上能够参加接触而构成运动副的表面
- 根据接触情况分类:
-
- 高副:通过单一点或线接触而构成的运动副
-
- 低副:通过面接触而构成的副
- 根据封闭方式分类:
-
- 几何封闭/形封闭运动副
-
- 力封闭运动副
- 根据构成运动副的两构件之间相对运动分类:
-
- 转动副/回转副/铰链
-
- 移动副
-
- 螺旋副
-
- 球面副
- 根据空间分类:
-
- 平面运动副
-
- 空间运动副
运动链(kinematic chain)
构件通过运动副的连接而构成的可相对运动的系统
机构
在运动链中,如果将其中某一构件加以固定而成为机架(fixed link),则该运动链便成为机构
原动件(主动件):机构中按给定的已知运动规律独立运动的构件
从动件:主动件外其余活动构件
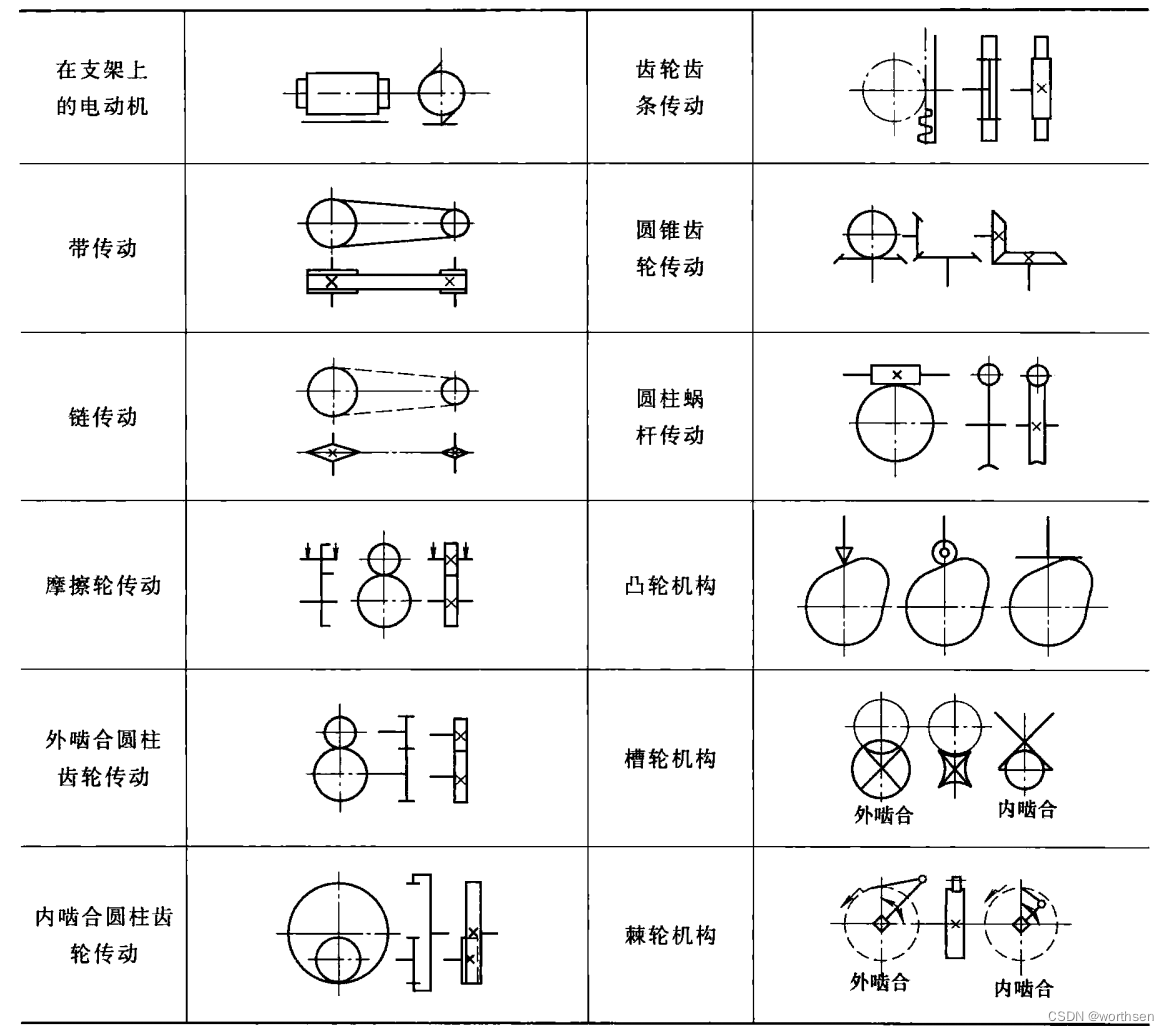
2-3 机构运动简图
kinematic diagram of mechanism
用以表示机构运动传递情况的简化图形:
根据机构的运动尺寸,按一定的比例尺定出各运动副的位置,用运动副及常用机构运动简图的代表符号和一般构件的表示方法将机构的运动传递情况表示出来
2-4 机构具有确定运动的条件及最小阻力定律
欠驱机构:原动件数小于机构自由度的机构
冗驱机构:原动件数多于机构自由度的机构
2-5 2-6 机构自由度的计算
F
=
3
n
−
(
2
P
1
+
P
h
−
p
′
)
−
F
′
F = 3n - (2P_1 + P_h - p') - F'
F=3n−(2P1+Ph−p′)−F′
自由度 = 3 * 活动构件数 - (2 * 低副数 + 高副数 - 虚约束数) - 局部自由度
复合铰链:
m 个构件在同一连接处构成复合铰链( m ≥ 2 ),则共有( m − 1 )个转动副。
复合高副:
如果两构件在多处相接触构成平面高副,而在各接触点处的公法线方向彼此不重合,就构成了符合高副,相当于一个低副。
局部自由度
在有些机构中,某些构件所产生的局部运动并不影响其他构件的运动,则称这种局部运动的自由度为局部自由度。
如滚子推杆凸轮机构中,滚子绕其自身轴线的转动并不影响其他构件的运动,只是一种局部自由度。
虚约束
有些运动副带入的约束对机构的运动只起重复约束作用,特把这类约束称为虚约束(redundant constraint)
2-7 平面机构的组成原理、结构分类及结构分析
3 平面机构的运动分析
3-2 用图解法作机构的运动分析
速度瞬心
矢量方程图解法/相对运动图解法
相似三角形计算原理:同一个构件上的三个点
4 平面机构的力分析
4-1 机构力分析
作用在机械上的力:
- 驱动力 (driving force)
-
- 驱动力与其作用点的速度方向相同或成锐角
-
- 作正功,称为驱动功/输入功(driving work)
- 阻抗力(resistance)
-
- 有效阻抗力:有效功
-
- 有害阻抗力:非生产阻力,损失功
4-3运动副中摩擦力的确定
移动副中摩擦力的确定:
当量摩擦因数
f
v
f_v
fv
摩擦角
φ
\varphi
φ :总反力与法向反力之间的夹角
φ = a r c t a n f \varphi = arctanf φ=arctanf
转动副中摩擦力的确定
摩擦圆(circle of friction)
ρ
=
f
v
r
\rho = f_vr
ρ=fvr
总反力与摩擦圆相切
5 机械的效率和自锁
5-1 机械的效率
机械效率
-
机械效率反映输入功在机械中的有效利用程度,以 η \eta η 表示:
-
功表述
η = W r W a = 1 − W f W d \eta = \frac{W_r}{W_a} = 1 - \frac{W_f}{W_d} η=WaWr=1−WdWf -
功率表述
η = P r P d = 1 − P f P d \eta = \frac{P_r}{P_d} = 1 - \frac{P_f}{P_d} η=PdPr=1−PdPf -
- P d P_d Pd 输入功率
-
- P r P_r Pr 输出功率
-
- P f P_f Pf 损失功率
-
损失率
ξ = W f W a = P f P d \xi = \frac{W_f}{W_a} = \frac{P_f}{P_d} ξ=WaWf=PdPf -
力表述
η = F 0 F \eta = \frac{F_0}{F} η=FF0 -
- 理想驱动力 F 0 F_0 F0
-
- 实际驱动力 F F F
-
力矩表述
η = M 0 M \eta = \frac{M_0}{M} η=MM0 -
- 理想驱动力矩 M 0 M_0 M0
-
- 实际驱动力矩 M M M
机组效率的计算
-
串联
串联机组的总效率等于组成该机组的各个机器效率的连乘积:
总效率小于其中任意机器的效率。
η = P r P d = P 1 P d P 2 P 1 . . . P k P k − 1 = η 1 η 2 . . . η k \eta = \frac{P_r}{P_d} = \frac{P_1}{P_d} \frac{P_2}{P_1}... \frac{P_k}{P_{k-1}} = \eta_1\eta_2...\eta_k η=PdPr=PdP1P1P2...Pk−1Pk=η1η2...ηk -
并联
并联机组的总效率计算公式为:
η = Σ P r i Σ P d i = P 1 η 1 + P 2 η 2 + . . . + P k η k P 1 + P 2 + . . . + P k \eta = \frac{\Sigma P_{ri}}{\Sigma P_{di}} = \frac{P_1 \eta1 + P_2 \eta2 + ... + P_k \eta k}{P_1 + P_2 + ... + P_k} η=ΣPdiΣPri=P1+P2+...+PkP1η1+P2η2+...+Pkηk
其中 η m i n < η < η m a x \eta_{min} < \eta < \eta_{max} ηmin<η<ηmax
机组总效率主要取决于传递功率最大的机器的效率。 -
混联
混联机组的效率计算为:
η = Σ P r Σ P d \eta = \frac{\Sigma P_r}{\Sigma P_d} η=ΣPdΣPr
5-2 机械的自锁
机械的自锁(self locking):由于摩擦的存在,无论一个驱动力如何增大,也无法让该机械沿着有效驱动力作用的方向运动的现象
移动副自锁条件:
β
≤
φ
\beta \leq \varphi
β≤φ
作用于滑块上的驱动力作用在其摩擦角之内
转动副自锁条件:
α
≤
ρ
\alpha \leq \rho
α≤ρ
作用在轴径上的驱动力为单力
F
F
F ,且作用于摩擦圆之内
机械自锁的判断
当驱动力任意增大时:
- G ≤ 0 G \leq 0 G≤0 能克服的生产阻抗力小于等于零
- η ≤ 0 \eta \leq 0 η≤0 效率小于等于零
则机械自锁
机械自锁的方向性:
机械的自锁只是在一定的受力条件和受力方向下发生的,而在另外的情况下是可动的
6 机械的平衡
6-1 机械平衡的目的及内容
机械平衡的目的:设法将构件的不平衡惯性力加以平衡以消除或减小其不良影响
机械平衡:
-
转子平衡
-
- 刚性转子
工作转速低于 ( 0.6 ∼ 0.75 ) n c 1 (0.6 \sim 0.75)n_{c1} (0.6∼0.75)nc1 ( n c 1 n_{c1} nc1 为转子的第一临界速度)
· 静平衡:惯性力平衡
· 动平衡:惯性力平衡 + 惯性力矩平衡
- 刚性转子
-
- 挠性转子:
工作转速高 [ n ≥ ( 0.6 ∼ 0.75 ) n c 1 ] [n \geq (0.6 \sim 0.75)n_{c1}] [n≥(0.6∼0.75)nc1]
工作过程中将会产生较大的弯曲变形,从而使其惯性力显著增大
- 挠性转子:
-
机构的平衡(机械在机座上的平衡)
6-2 刚性转子的平衡计算
刚性转子的静平衡计算:
-
盘状转子
转子轴向宽度 b 与其直径 D 之比 b D < 0.2 \frac b{D} < 0.2 Db<0.2
齿轮、盘形凸轮、带轮、叶轮、螺旋桨等
质量可近似认为分布在垂直于其回转轴线的同一平面内 -
在转子上增加或除去一部分质量,使其质心与回转轴心重合
-
静平衡条件
Σ F = Σ F I i + F b = 0 \Sigma F = \Sigma F_{Ii} + F_b = 0 ΣF=ΣFIi+Fb=0
设平衡质量 m b m_b mb 的矢径为 r b r_{b} rb,则式可化为
m 1 r 1 + m 2 r 2 + . . . + m i r i + m b r b = 0 m_1 r_1 + m_2 r_2 + ... + m_i r_i + m_b r_b= 0 m1r1+m2r2+...+miri+mbrb=0
式中
m
r
r
i
m_r r_i
mrri 称为质径积
平衡质径积大小:
m
b
r
b
=
(
m
b
r
b
)
x
2
+
(
m
b
r
b
)
y
2
m_b r_b =\sqrt{(m_b r_b)^2_x + (m_b r_b)^2_y}
mbrb=(mbrb)x2+(mbrb)y2
根据转子结构选定
r
b
r_b
rb(一般选大一些)之后,即可定出平衡质量
m
b
m_b
mb ,其相位角
α
b
\alpha_b
αb
α
b
=
a
r
c
t
a
n
[
(
m
b
r
b
)
y
(
m
b
r
b
)
x
]
\alpha_b = arctan[\frac{(m_b r_b)_y}{(m_b r_b)_x}]
αb=arctan[(mbrb)x(mbrb)y]
- 在同一个平衡面内增加或者去除一个平衡质量即可获得平衡,故又称为单面平衡
刚性转子的动平衡计算:
- 转子动平衡条件:
各偏心质量产生的惯性力矢量和为零,这些惯性力所构成的力矩矢量和也为零,即
Σ F = 0 , Σ M = 0 \Sigma F = 0, \Sigma M = 0 ΣF=0,ΣM=0
只要在两个平衡基面内分别加上或除去一个适当的平衡质量,即可得到完全平衡。故动平衡又称为双面平衡
两平衡基面间的距离应适当大一些
6-3 刚性转子的平衡实验
静平衡实验:
使转子的质心落在其回转中心上
动平衡实验:
动平衡机(dynamic balancing machine)
现场平衡(field balancing):
在现场通过直接测量机器中转子支架的振动,来确定不平衡量的大小及方位,进而进行平衡。
6-4 转子的许用不平衡量和许用不平衡度
许用不平衡量
[
m
r
]
(
g
.
m
m
)
[mr](g.mm)
[mr](g.mm)
许用不平衡量
[
e
]
(
μ
m
)
[e](\mu m)
[e](μm)
[
e
]
=
[
m
r
]
m
[e] = \frac{[mr]}m
[e]=m[mr]
式中,m——转子质量,kg;r——偏心质量回转半径,mm。
转子平衡精度用转子平衡品质等级表示
查表可知转子平衡品质量级
(
e
ω
)
(
m
m
s
)
(e \omega)(\frac{mm}s)
(eω)(smm),再用下两式可分别求得许用不平衡度和许用不平衡量
[
e
]
=
100
(
e
ω
)
ω
[e] = \frac{100(e \omega)}{\omega}
[e]=ω100(eω)
[
m
r
]
=
(
e
)
m
[mr] = (e)m
[mr]=(e)m
式中,
ω
\omega
ω ——转子角速度,rad/s;m ——转子质量,kg
6-5 平面机构的平衡
机构的平衡条件:
机构的总惯性力
F
1
F_1
F1 和 总惯性力矩
M
1
M_1
M1 分别为零
F
1
=
0
,
M
1
=
0
F_1 = 0, M_1 = 0
F1=0,M1=0
只讨论总惯性力的平衡问题
欲使总惯性力
F
1
=
0
F_1 = 0
F1=0,则应使机构的质心静止不动
完全平衡:
- 利用平衡机构平衡
- 利用平衡质量平衡
要完全平衡 n 个构件的单自由度机构的惯性力,应至少加 n/2 个平衡质量,机构质量大大增加和带来其他问题,故在工程实际上往往采用部分平衡法
部分平衡:
- 利用平衡机构平衡
- 利用平衡质量平衡
- 利用弹簧平衡
7 机械的运转及其速度波动的调节
7-1 概述
应设法将机械运转速度波动的程度限制在许可的范围之内。
机械运转的三个阶段:
(1)启动阶段(starting period of machinery)
(2)稳定运转阶段(steady motion period of machinery)
- 平均角速度 ω m \omega_m ωm 保持为一个常数
- ω m \omega_m ωm 一般周期性波动
- 机械的一个运动循环:机械原动件角速度变化的一个周期
(3)停车阶段(stopping period of machinery)
机械特性(mechanical behavior):各种原动机的作用力/力矩与其运动参数(位移、速度)之间的关系
7-4 稳定运转状态下机械的周期性速度波动及其调节
盈功(increment of work)
- 驱动功 大于 阻抗功
- 等效构件动能增加
- 等效构件角速度上升
亏功(decrement of work)
- 驱动功 小于 阻抗功
- 等效构件动能减小
- 等效构件角速度下降
∫ φ b φ c ( M e d − M e r ) d φ = J c a ′ ω c ′ 2 2 − J c a ω a 2 2 = 0 \int\limits_{\varphi_{b}}^{\varphi_{c}}(M_{ed} - M_{er})d_{\varphi} = \frac{J_{ca}'\omega'^2_c}2 - \frac{J_{ca}\omega^2_a}2 = 0 φb∫φc(Med−Mer)dφ=2Jca′ωc′2−2Jcaωa2=0
周期性速度波动的调节
飞轮(Flywheel)
- 最好将飞轮安装在机械的高速轴上
- 机械出现盈功时,飞轮加速,储能;机械亏功时,飞轮减速,放能
- 飞轮等效转动惯量
J
f
J_f
Jf 的计算公式:
J f ≥ Δ W max ω m [ δ ] − J e J_f \geq \frac{\Delta W_{\text{max}}}{\omega_m [\delta]} - J_e Jf≥ωm[δ]ΔWmax−Je
如果 J e ≪ J F J_e \ll J_F Je≪JF ,则 J e J_e Je 可以忽略不计,于是可近似写为:
J F ≥ Δ W max ω m 2 [ δ ] J_F \geq \frac{\Delta W_{\text{max}}}{\omega_m^2 [\delta]} JF≥ωm2[δ]ΔWmax
又如果平均角速度 ω m \omega_m ωm 用平均转速 n (单位:r/min)代换,则有:
J F ≥ 900 Δ W max π 2 n 2 [ δ ] J_F \geq \frac{900 \Delta W_{\text{max}}}{\pi^2 n^2 [\delta]} JF≥π2n2[δ]900ΔWmax
8 连杆机构及其设计
8-1 连杆机构及其传动特点
连杆机构特点:
原动件的运动都要经过一个不与机架直接相连的中间构件(连杆 coupler),才能传动从动件
连杆机构传动优点:
- 运动副一般均为低副。运动副元素为面接触,压强小,承载能力大,润滑好,磨损小,加工制造容易。连杆机构中的低副一般几何封闭,有利于工作的可靠性
- 故连杆机构又被称为 低副机构 (lower pair mechanism)
- 原动件运动规律不变的条件下,可以改变各构件的相对长度,来使从动件得到不同的运动规律
- 连杆曲线 形状随着各构件相对长度的改变而改变,形式多种多样,可用来满足一些特定工作的需要
- 容易改变运动传递方向、扩大行程、实现增力、远距离传动等
连杆机构缺点:
- 传动路线长:易产生较大的误差积累、降低机械效率
- 惯性力难以用一般平衡方法加以消除,因而不适用于高速运动
- 为满足一些运动规律和运动轨迹的设计要求,设计十分繁难
连杆机构分类(按各构件间相对运动空间关系):
- 平面连杆机构
- 空间连杆机构
8-2 平面四杆机构的类型及应用
连杆架(side link):
- 与机架相连的杆
- 如果能做整周回转则称为曲柄 (crank)
- 如果只能在一定范围内摆动则称为摇杆(rocker)
曲柄摇杆机构:
- 两个连架杆一为曲柄一为摇杆
双曲柄机构:
-
两个连架杆均为曲柄
-
若相对两杆长度相等:
-
- 且平行,则构成平行四边形机构
-
-
- 两曲柄以相同速度同向转动
-
-
-
- 连杆作平动
-
-
-
- 连杆上任一点的轨迹均为以曲柄长度为半径的圆
-
-
- 但不平行,构成逆平行四边形机构
双摇杆机构:
- 两个连架杆都是摇杆
- 若两摇杆长度相等且最短,则构成等腰梯形机构
曲柄滑块机构
正弦机构
偏心轮机构
8-3 平面四杆机构的基本知识
有曲柄的条件:
-
满足杆长条件
最短杆长度 + 最长杆长度 ≤ 其余两杆长度之和 -
最短杆为连杆架/机架
急回运动和形成速度变化系数:

- 极位:摇杆处于极限位置
- 极位夹角 θ
- 急回运动
- 行程速度变化系数/行程速比系数 K
K = ( 180 ° + θ ) ( 180 ° − θ ) K = \frac{(180° + \theta)}{(180° - \theta)} K=(180°−θ)(180°+θ)
压力角和传动角(pressure angle, transmission angle):
压力角 α \alpha α:力与速度正方向之间的夹角,越大越好
传动角 γ \gamma γ :压力角的余角,越小越好
死点(dead point):
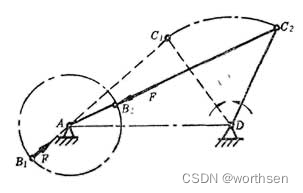
- 传动角 γ = 0 ° \gamma = 0° γ=0°
- 主动件通过连杆作用于从动件上的力恰好通过其回转中心,出现不能使从动件转动的“顶死”现象
- 机构的极位和死点是同一位置(机构原动件不同)
- 极位附近可获得很大的增力效果
铰链四杆机构的连杆曲线
铰链四杆机构的运动连续性
8-4平面四杆机构的设计
9 凸轮机构及其设计
9-1 凸轮机构的应用及分类
- 凸轮(cam):通常作主动件作等速转动
- 推杆(从动件,follower):被凸轮直接推动的构件
- 反凸轮机构(inverse cam mechanism):凸轮为从动件
凸轮机构的分类:
按凸轮形状
- 盘形凸轮:一个具有变化向径的盘形构件绕固定轴线回转
- 圆柱凸轮:在圆柱面上开有曲线凹槽,或在圆柱端面上作出曲线轮廓

按推杆形状
- 尖顶推杆:构造最简单,但易磨损
- 滚子推杆:摩擦较小,可用来传递较大的动力
- 平底推杆:凸轮与平底的接触面间易形成油膜,润滑性好,常用于高速传动
按推杆运动形式
- 直动推杆
-
- 对心直动推杆
-
- 偏置直动推杆
- 摆动推杆
按凸轮与推杆保持接触的方法不同
-
力封闭:利用推杆的重力、弹簧力来使推杆与凸轮保持接触
-
几何封闭:利用凸轮或推杆的特殊几何结构使保持接触
-
- 沟槽凸轮、
-
- 等宽凸轮机构
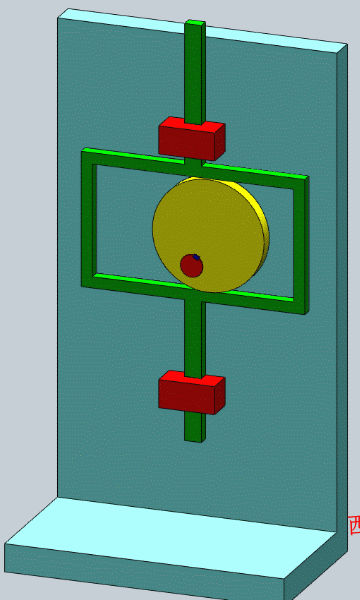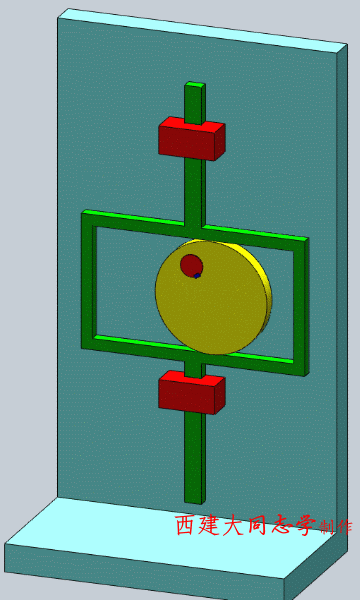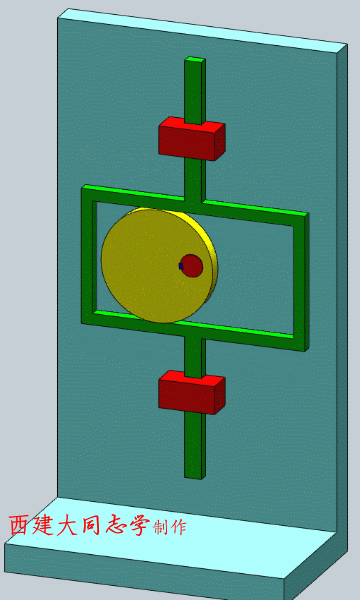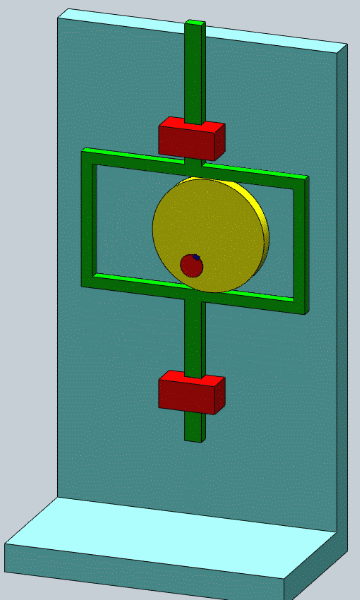
- 等宽凸轮机构
-
- 等径凸轮机构
-
- 共轭凸轮(主回凸轮,conjugate cam)
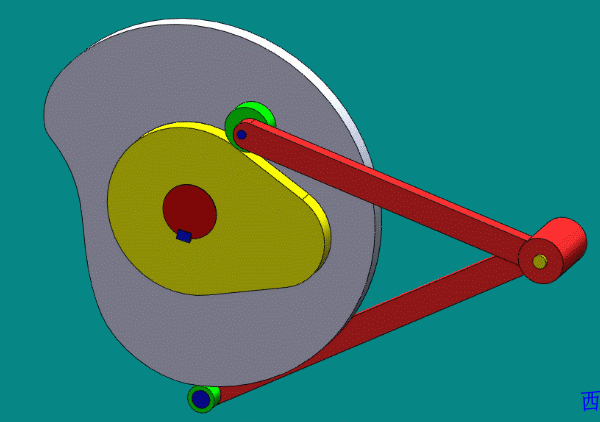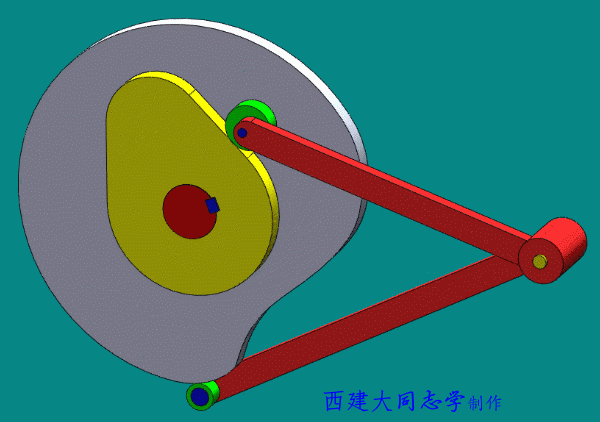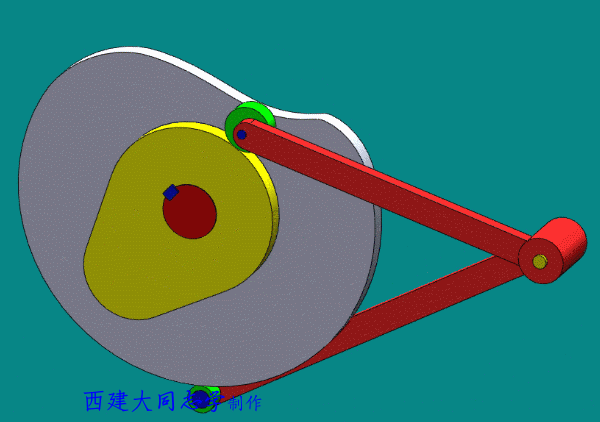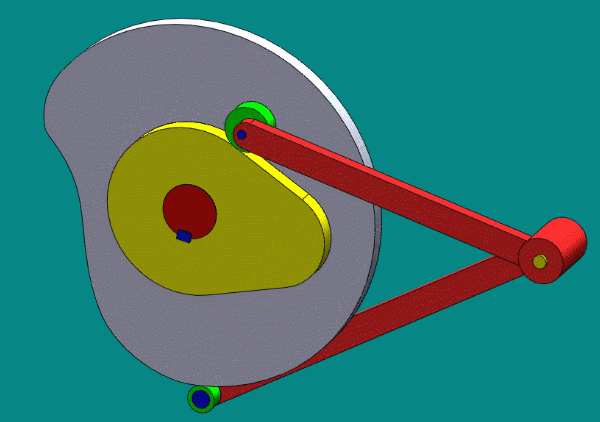
- 共轭凸轮(主回凸轮,conjugate cam)
9-2 推杆的运动规律
| 描述 | 符号 | 说明 |
|---|---|---|
| 基圆 | ( r_0 ) | 以凸轮最小半径所做的圆 |
| 推程运动角 | ( \delta_0 ) | 推杆由最低位置被推到最高位置(推程)对应的凸轮转角 |
| 远休止角 | ( \delta_{01} ) | 推杆在最高位置静止不动(远休止)对应的凸轮转角 |
| 回程运动角 | ( \delta’_0 ) | 推杆由最高位置回最低位置(回程)对应的凸轮转角 |
| 近休止角 | ( \delta_{02} ) | 推杆在最低位置静止不动(近休止)对应的凸轮转角 |
| 推程 | ( h ) | 推杆在推程或回程中移动的距离 |
推杆运动规律:
推杆的位移 ( s ) 、速度 ( v ) 和加速度 ( a ) 随凸轮转角 ( \delta ) 变化的规律
刚性冲击
速度突变,推杆理论上将出现无穷大的加速度和惯性力
柔性冲击
加速度有突变,但为有限值,引起的冲击较小
多项式运动规律
-
一般表达式:
[ s = C_0 + C_1 \delta^1 + C_2 \delta^2 + … + C_n \delta^n ] -
- ( \delta ) —— 凸轮转角
-
- ( s ) —— 推杆位移
-
- ( C_0, C_1, C_2, …, C_n ) —— 待定系数,利用边界条件等来确定
-
一次多项式运动规律
-
- 等速运动规律
-
- 有刚性冲击
-
二次多项式运动规律
-
- 等加速等减速运动规律
-
- 有柔性冲击
-
五次多项式运动规律
-
- 无刚性冲击、无柔性冲击
三角函数运动规律
-
余弦加速度运动规律/简谐运动规律
- 有柔性冲击、无刚性冲击
-
正弦加速度运动规律/摆线运动规律
- 无刚性冲击、无柔性冲击
- 加速度最大值最大
9-3 凸轮轮廓曲线的设计
设计方法所依据的基本原理:反转法
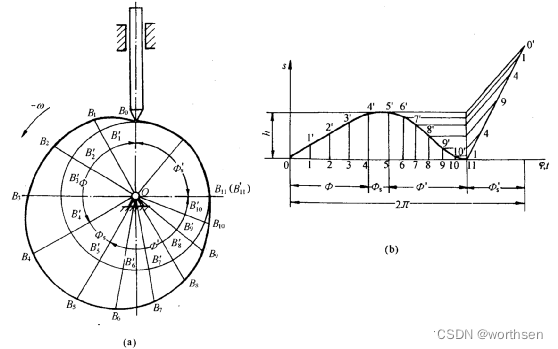
设计方法:图解法、解析法
理论廓线(cam pitch curve)
- 滚子中心A在推杆复合运动中的轨迹
- 凸轮的基圆半径若未指明,通常系指理论廓线的最小半径
实际廓线(cam contour)
- 又称工作廓线
- 以理论廓线上一系列点为圆形,以滚子半径 ( r_r ) 为半径,作一系列的圆,再作此圆族的包络线,即为凸轮的实际廓线
- 理论廓线向外延伸一个滚子半径长度得到的廓线
9-4 凸轮机构基本尺寸的确定
基圆半径、滚子半径、平底尺寸、压力角
压力角
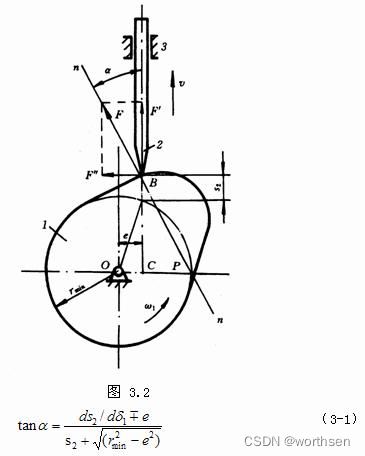
- 推杆沿凸轮廓线接触点的法线方向与推杆速度方向之间所夹的锐角
- 临界压力角 ( \alpha_c = \arctan\left[\frac{1}{1+\frac{2b}{l}\tan\varphi_2}\right] - \varphi_1 )
通过增大导轨长度l,减小悬臂尺寸b,可以提高临界压力角
- 许用压力角[a]
-
- 推程时:
-
-
- 直动推杆 [α] = 30°
-
-
-
- 摆动推杆 [α] = 30° ~ 45°
-
-
- 回程时:70° ~ 80°
基圆半径的确定
在偏距一定、推杆的运动规律已知的条件下,加大基圆半径 ( r_0 ) 可以减小压力角 ( \alpha ) ,从而改善机构的传力特性,但此时机构的尺寸将会增大。
变尖与失真
- 理论廓线曲率半径 ( \rho ) ;滚子半径 ( r_r ) ;工作廓线曲率半径 ρ a \rho_a ρa; ( \rho_a = \rho + r_r )
- 如果 ( \rho = r_r ) , ( \rho_a = 0 ),工作廓线出现尖点,称为变尖现象
- 当 ( \rho < r_r ) ,工作廓线出现交叉,致使推杆不能按预期的运动规律运动,称为失真现象
10 齿轮机构及其设计
10-1 齿轮机构的特点及类型
优点:
- 传递功率范围大
- 传动效率高
- 传动比精确
- 使用寿命长
- 工作可靠
缺点:
- 对制造和安装精度要求高
- 成本较高
用于平行轴间传动的齿轮机构
- 外啮合齿轮机构:两轮转向相反
- 内啮合齿轮机构:两轮转向相同
- 齿轮与齿条机构:齿条可视为轴心在无穷远处的圆形齿轮
- 直齿轮:轮齿的齿向与齿轮轴线方向一致
- 斜齿轮:轮齿的齿向相对于齿轮轴线倾斜一个角度
- 人字齿轮:可视为由螺旋角方向相反的两个斜齿轮所组成
用于相交轴间传动的齿轮机构
- 锥齿轮机构:直齿应用最广,曲线齿传动平稳承载能力高
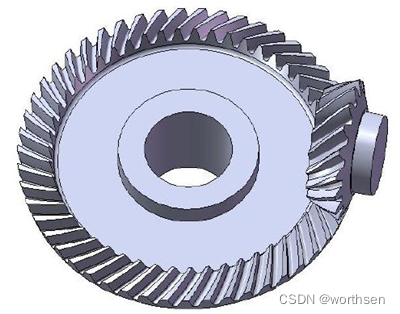
用于交错轴间传动的齿轮机构
- 交错齿轮机构(crossed helical gear mechanism)
- 蜗杆机构(worm and worm wheel mechanism)
- 准双曲面齿轮机构(hypoid gear mechanism)
10-2 齿轮的齿廓曲线
齿廓(tooth profile):圆柱齿轮的齿面与垂直于其轴线的平面的交线
齿廓啮合基本定律:相互啮合传动的一对齿轮,在任一位置时的传动比,都与其连心线 O 1 O 2 O1 O2 O1O2 被其啮合齿廓在接触点处的公法线所分成的两线段长成反比
故齿轮的瞬时传动比与齿廓形状有关

节点(pitch piont):齿廓公法线 nn 与两轮连心线 O 1 O 2 O1 O2 O1O2 的交点 P
两齿轮作定传动比传动的条件:不论两齿廓在何位置接触,过接触点所作的两齿廓公法线与两齿轮的连心线交于一定点
节圆(pitch circle):定传动比传动时节点 P 在轮的运动平面上的轨迹圆
节线:变传动比传动时节点 P 在轮运动平面上的轨迹(一条非圆曲线)
共轭齿廓(conjugate tooth profile):能按预定传动比规律相互啮合传动的一对齿廓
理论上,对于预定传动比,只要给定任一齿轮的齿廓曲线和中心距,就可根据齿廓啮合基本定律求出与其啮合传动的另一齿轮上的共轭齿廓曲线
(定传动比传动)常用的齿廓曲线(按顺序):
(1)渐开线
(2)摆线
(3)变态摆线
(4)圆弧齿廓、抛物线齿廓、余弦齿廓等
10-3 渐开线齿廓及其啮合特点
渐开线(involute)
基圆(base circle)、发生线(generating line)、展角(evolving angle)
特性:
- 发生线上
- 渐开线上任一点
- 渐开线形状取决于基圆大小
- 基圆以内无渐开线
渐开线方程式:
- 压力角
α
K
\alpha_K
αK
[ \cos \alpha_K = \frac{r_b}{r_k} ]
渐开线函数:
[ \text{inv}\alpha_K = \theta_k = \tan \alpha_K - \alpha_K ]
渐开线齿廓的啮合特点:
- 传动的可分性:渐开线齿廓传动比不受中心距变化的影响
- 渐开线齿廓之间的正压力方向不变
啮合线(line of action):齿廓接触点在固定平面中的轨迹
10-4 渐开线标准齿轮的基本参数和几何尺寸
齿轮各部分的名称和符号:
| 名称 | 符号 | 说明 | 英文 |
|---|---|---|---|
| 齿顶圆 | r α r_{\alpha} rα(半径) d α d_{\alpha} dα(直径) | 过轮齿顶端所作的圆 | tip or addendum circle |
| 齿根圆 | ( r_f d_f ) | 过轮齿槽底所作的圆 | root circle |
| 齿厚 | ( S_i ) | 任意圆周上一个轮齿两侧齿廓间的弧线长度 | tooth thickness |
| 齿槽宽 | ( e_i ) | 任意圆周上齿槽两侧齿廓间的弧线长度 | space width |
| 齿距 | ( P_i ) , ( P_i = S_i + e_i ) | 任意圆周上相邻两齿同侧齿廓之间的弧线长 | pitch |
| 分度圆 | ( r\ d\ s\ e\ p ) | 为了便于齿轮设计和制造而选择的一个尺寸参考圆 | reference circle |
| 齿顶高 | ( h_{a} ) | 齿轮介于分度圆与齿顶圆之间的部分(齿顶)的径向高度 | addendum |
| 齿根高 | ( h_{f} ) | 齿轮介于分度圆与齿根圆之间的部分(齿根)的径向高度 | dedendum |
| 齿全高 | ( h ) ,( h = h_a + h_f ) | 齿顶高 + 齿根高 | tool depth |
渐开线齿轮的基本参数:
齿数(number of teeth)
齿轮在整个圆周上轮齿的总数,用
z
z
z 表示
模数(module)
齿距 p 与 π 的比值,用 m 表示
$ m = p / π $
故齿轮的分度圆直径 d 可表示为
$ d = mz $
(1)分度圆压力角(压力角)
- α = a r c c o s ( r b / r ) \alpha = arccos(r_b / r) α=arccos(rb/r)
- r b = r c o s α = z m 2 c o s α r_b = rcos\alpha = \frac{zm}{2}cos\alpha rb=rcosα=2zmcosα
- GB/T 1356-2001 规定
- 在一些特殊场合 α 也允许取其他值
(2)齿顶高系数(addendum coefficient) - 齿轮的齿顶高与其模数比值
- 用 h a ∗ h^*_a ha∗ 表示
- GB/T 1356-2001 规定 h a ∗ = 1 h^*_a = 1 ha∗=1
(3)顶隙系数(clearance coefficient)
- 顶隙(一个齿轮的齿顶圆与另一个齿轮齿根圆之间的径向距离)与模数的比值
- 用 c ∗ c^* c∗
- GB/T 1356-2001 规定 c* = 0.25
渐开线标准齿轮:
- m 、 α 、 h ∗ a 、 c ∗ m、\alpha、h^*a、c^* m、α、h∗a、c∗ 均为标准值
- 分度圆齿厚等于齿槽宽
- 渐开线齿轮
10-5 渐开线直齿圆柱齿轮的啮合传动
一对渐开线齿轮正确啮合的条件:两轮的模数和压力角应分别相等
齿轮传动的中心距:
-
保证两轮的顶隙为标准值
-
- 顶隙(bottom clearance)
-
- c = c ∗ m c = c^*m c=c∗m
-
保证两轮的理论齿侧间隙为零
-
- 齿侧间隙(backlash):很小,由制造公差保证;理论计算齿轮名义尺寸、中心距时按零考虑
-
- 使一个齿轮在节圆上的齿厚等于另一个齿轮在节圆上的齿槽款
标准中心距 = 两轮分度圆半径之和
a
=
r
1
+
r
2
a = r_1 + r_2
a=r1+r2
齿轮传动的啮合角(working pressure angle):
- 节点 P 的圆周速度方向与啮合线 N 1 N 2 N_1 N_2 N1N2 之间所夹锐角
- 用 α ′ \alpha' α′ 表示
- 当两轮按标准中心距安装,啮合角等于分度圆压力角,即 a′ = a 时, α ′ = α \alpha' = \alpha α′=α
- 实际中心距 a′ 与标准中心距 a 不相同时,有如下关系
a ′ c o s α ′ = a c o s α a' cos\alpha' = a cos\alpha a′cosα′=acosα
连续传动条件:要求在前一对齿脱开啮合之前,后一对齿已进入啮合
重合度(contact radio):
- εα = 实际啮合线段/法向齿距
- 大于等于许用值 ε α ≥ [ ε α ] \varepsilon\alpha \geq [\varepsilon \alpha] εα≥[εα]
- 重合度随齿数 z z z 的增多而增大;当 z z z 趋于无穷,极限重合度 ε α max = 1.981 \varepsilon_{\alpha \text{max}} = 1.981 εαmax=1.981
10-6 渐开线齿廓的切制原理与根切现象
近代齿轮加工方法中最常用切削加工法
切削加工法:
-
仿形法:
铣床加工 -
范成法(展成法)
-
- 插齿
-
- 滚齿
-
- 磨齿
-
利用齿廓啮合基本定律来切制齿廓
根切:
范成法加工时,有时刀具的顶部会过多地切入齿轮根部,因而将齿根的渐开线齿廓切去一部分
应避免严重根切
标准齿轮不发生根切的最少齿数:
z
m
i
n
=
2
h
a
∗
s
i
n
2
α
z_{min} = \frac{2h^*_a}{sin^2\alpha}
zmin=sin2α2ha∗
当
h
∗
a
=
1
、
α
=
20
°
h^*a = 1、\alpha = 20°
h∗a=1、α=20°时,
z
m
i
n
=
17
z_{min} = 17
zmin=17
10-7 渐开线变位齿轮简介
标准齿轮缺点:
- 要求齿轮齿数 z ≥ z m i n z \geq z_{min} z≥zmin ,否则将产生根切现象
- 不适用于中心距 a ′ ≠ a = m ( z 1 + z 2 ) / 2 a' \neq a = m(z_1 + z_2) / 2 a′=a=m(z1+z2)/2 的场合
- 一对相互啮合的标准齿轮中,小齿轮齿廓渐开线曲率半径小齿根厚度薄,参与啮合的次数又多,强度低易损坏
为了改善标准齿轮的上述不足,就要做一定的修正,最广泛采用的是变位修正法
径向变位量:
- 在加工齿轮时,将齿条刀具由标准位置相对于轮坯中心向外移出一段距离 xm,即径向变位量
- 径向变位量(xm) = 径向变位系数(x) × 模数(m)
- 正变位(齿轮):x为正值,刀具由齿轮轮坯中心移远;反之为负变位(齿轮)
避免发生根切的最小变位系数:
x
m
i
n
=
h
a
∗
(
z
m
i
n
−
z
)
/
z
m
i
n
x_{min} = h^*_a(z_{min} - z)/z_{min}
xmin=ha∗(zmin−z)/zmin
变位齿轮的几何尺寸:
齿厚
齿槽宽
齿根高
齿顶高
齿顶圆半径
中心距:
a
c
o
s
α
=
a
′
c
o
s
α
′
acos\alpha = a'cos\alpha'
acosα=a′cosα′
无侧隙啮合方程(equation of engagement with zero backlash)
i
n
v
α
′
=
2
t
a
n
α
(
x
1
+
x
2
)
/
(
z
1
+
z
2
)
+
i
n
v
α
inv \alpha' = 2 tan\alpha(x_1 + x_2)/(z_1 + z_2) + inv \alpha
invα′=2tanα(x1+x2)/(z1+z2)+invα
公式中:
- z 1 、 z 2 z_1、z_2 z1、z2 —— 两轮齿数
- α —— 分度圆压力角
- invα、invα′ —— α、α′ 的渐开线函数(其值可由已有的渐开线函数表查取)
- x 1 、 x 2 x_1、x_2 x1、x2 —— 两轮的变位系数
正传动:
- 减小齿轮机构的尺寸
- 齿轮机构承载能力有较大提高
- 重合度减小较多(缺点)
负传动:
- 重合度略有增加
- 齿轮强度下降
- 只用于配凑中心距这种特殊需要场合中
10-8 斜齿圆柱齿轮传动
螺旋角 β (helix angle):
斜齿轮的齿廓曲面与其分度圆柱面相交的螺旋线的切线与齿轮轴线之间所夹的锐角
法面参数 -> 标准值
端面参数 -> 几何尺寸
标准中心距
a
=
(
d
1
+
d
2
)
/
2
=
m
n
(
z
1
+
z
2
)
/
(
2
c
o
s
β
)
a = (d_1 + d_2) / 2 = m_n(z_1 + z_2)/(2 cos\beta)
a=(d1+d2)/2=mn(z1+z2)/(2cosβ)
斜齿轮的当量齿轮(virtual gear)与当量齿数
斜齿轮传动优缺点:
- 啮合性能好,传动平稳,噪声小
- 重合度大,降低每对轮齿的载荷,提高齿轮承载能力
- 不产生根切的最少齿数少
缺点:产生轴向推力 F a = F t t a n β F_a = F_t tan\beta Fa=Fttanβ
10-9 直齿锥齿轮传动
通常取锥齿轮大端的参数值为标准值
一对锥齿轮正确啮合条件:
两轮大端的模数和压力角分别相等
10-10 蜗轮蜗杆传动
蜗轮蜗杆传动特点:
- 传动特别平稳,啮合冲击小,噪声小
- 单级传动可获得较大的传动比,且结构紧凑
- 摩擦磨损大,传动效率低,易出现发热现象,需要用减摩耐磨材料来制造蜗轮,成本较高
- 当蜗杆导程角 γ 1 \gamma_1 γ1 小于啮合齿轮间的当量摩擦角 φ v \varphi_v φv 时,机构反行程具有自锁性
蜗轮蜗杆正确啮合的条件:
(阿基米德蜗轮蜗杆)
蜗轮蜗杆正确啮合的条件:(阿基米德蜗轮蜗杆)
m x 1 = m t 2 = m , α x 1 = α t 2 = α m_{x1} = m_{t2} = m, \alpha_{x1} = \alpha_{t2} = \alpha mx1=mt2=m,αx1=αt2=α
式中:
- m x 1 m_{x1} mx1 - 蜗杆的导程角
- m t 2 m_{t2} mt2 - 蜗轮的端面模数
- m m m 标准值
- α x 1 \alpha_{x1} αx1 - 蜗杆的压力角
- α t 2 \alpha_{t2} αt2 - 蜗轮的压力角
- α - 标准值
当蜗轮与蜗杆的轴线交错角 Σ = 90 ° \Sigma = 90° Σ=90° 时,还需保证 γ 1 = β 2 \gamma_1 = \beta_2 γ1=β2(蜗杆导程角 = 蜗轮的螺旋角)、两者螺旋线的旋向相同
11 齿轮系及其设计
11-1 齿轮系及其分类
齿轮系:
由一系列的齿轮所组成的齿轮传动系统,简称轮系
(1)定轴轮系
- 在轮系运转时,其各个齿轮的轴线相对于机架的位置都是固定的
(2)周转轮系
- 在轮系运转时,其中至少有一个齿轮轴线的位置并不固定,而是绕着其他齿轮的固定轴线回转
- 基本构件:太阳轮、行星轮
- 自由度为2——差动轮系;自由度为1——行星轮系
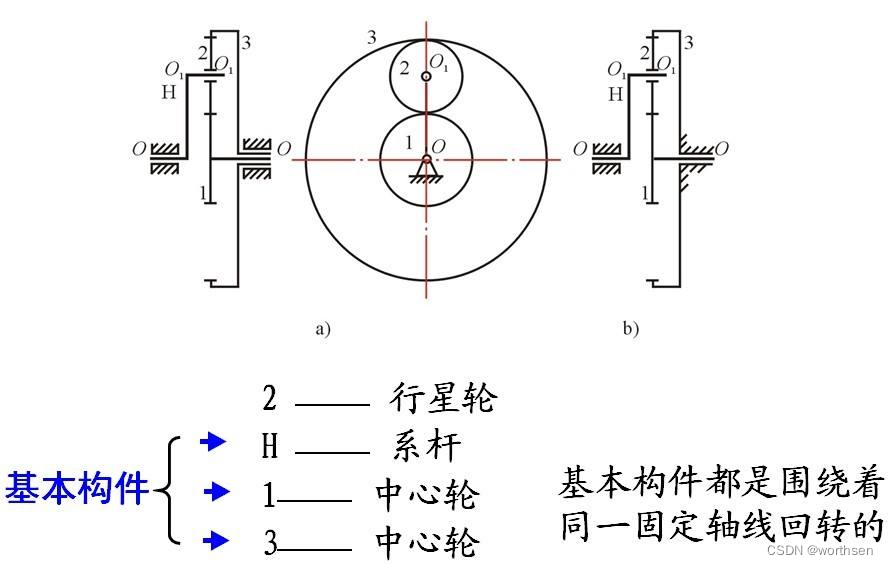
(3)复合轮系
- 既包含定轴轮系部分,又包含周转轮系部分
11-2 定轴轮系的传动比
定轴轮系的传动比 = 所有从动轮齿数的连乘积 / 所有主动轮齿数的连乘积
11-3 周转轮系的传动比
设周转轮系中的两个太阳轮分别为 m和n,行星架为 H,则其转化轮系的传动比
i
m
n
H
i^H_{mn}
imnH
i
m
n
H
=
ω
m
H
ω
n
H
=
ω
m
−
ω
H
ω
n
−
ω
H
i^H_{mn} = \frac{\omega^H_m}{\omega^H_n} = \frac{\omega_m -\omega_H}{\omega_n - \omega_H}
imnH=ωnHωmH=ωn−ωHωm−ωH = ± (在转化轮系中由m至n各从动轮齿数的乘积) / (在转化轮系中由m至n各主动轮齿数的乘积)
对于已知周转轮系来说,其转化轮系的传动比 i m n H i^H_{mn} imnH 的大小和“±”号均可定出。
如果所研究的轮系为具有固定轮的行星轮系,设固定轮为n,即
ω
n
=
0
\omega_n = 0
ωn=0,则式可改写为
i
m
n
H
=
ω
m
−
ω
H
0
−
ω
H
=
−
i
m
H
+
1
i^H_{mn} = \frac{\omega_m - \omega_H}{0 - \omega_H} = -i_{mH} + 1
imnH=0−ωHωm−ωH=−imH+1
i
m
H
=
1
−
i
m
n
H
i_{mH} = 1 - i^H_{mn}
imH=1−imnH
11-4 复合轮系的传动比
将定轴轮系和周转轮系的部分分开,分别计算各部分再联立求解
11-5 轮系的功用
- 实现分路传动
- 获得较大的传动比
- 实现变速传动
- 实现换向传动
- 用作运动的合成
- 用作运动的分解
12 其他机构
12-1 棘轮机构
ratchet mechanism

组成:
- 摇杆 1
- 棘爪(pawl) 2
- 棘轮(ratchet) 3
- 止动爪 4
- 弹簧 5:使止动爪和棘轮保持接触
特点:
- 结构简单、制造方便
- 运动可靠
- 棘轮轴每次转过角度的大小可以在较大的范围内调节
- 工作时有较大冲击和噪声
- 运动精度差
- 常用于速度较低和载荷不大的场合




12-2槽轮机构
geneva mechanism
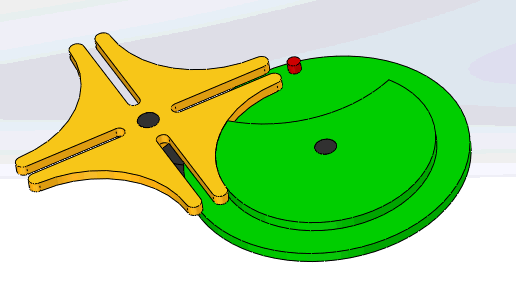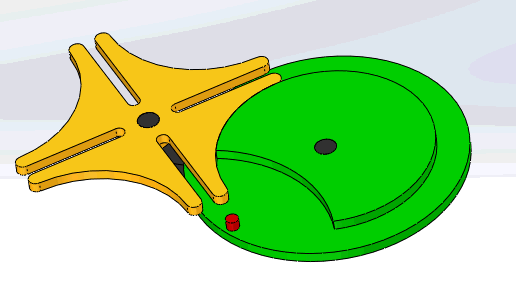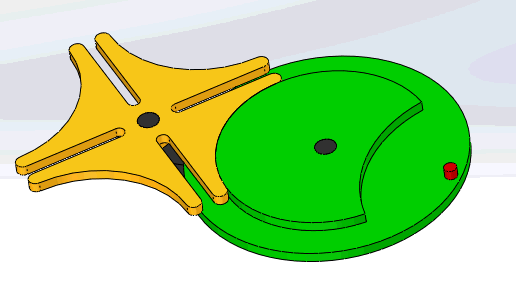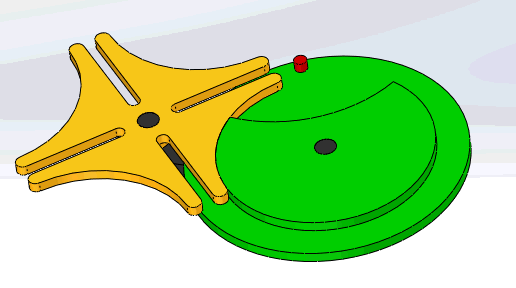

构成:
- 主动拨盘 1
- 从动槽轮 2
- 机架
特点:
- 结构简单、外形尺寸小
- 机械效率高
- 较平稳地间歇转动
- 有柔性冲击
- 常用于速度不太高的场合
普通槽轮机构:
- 槽轮上的槽均匀分布
- 用于传递平行轴之间的运动
球面槽轮机构:
- spherical Geneva mechanism
- 在两相交轴之间进行间歇传动

12-4 凸轮式间歇运动机构
12-5 不完全齿轮机构
参考
1、《机械原理:第八版》 孙恒、陈作模、葛文杰主编(西北工业大学 机械原理及机械零件教研室)
2、机械原理知识整理
3、Monograph-on-Theory-of-Machine-Raman-Gahlaut
4、Theory of Machines and Mechanisms ( PDFDrive )