写在最前，本文为实战向，解决问题的求法，理论基础见我的上一篇博客,当然了，只做题的话，看这个就够用了

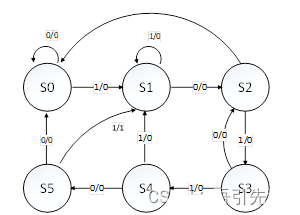
NFA转换为DFA

前置知识，首先得会求ε闭包和状态转换弧集
先看一道例题

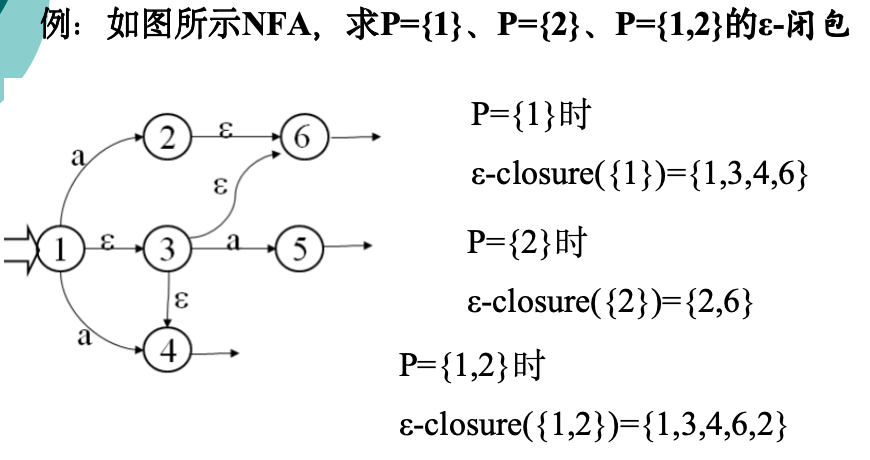
如何求ε-闭包？

求ε闭包需要我们，遍历集合的每一个元素，将每一个可由ε到达当元素，加入到新的闭包集合中，再继续探索新加入的点，是否还有可由ε到达当另一个新元素，直到不重不漏的将原集合的每个元素遍历完并且新加入的元素也找完。
注意的是：原先集合元素本身，也要加入到ε-闭包中，也就是意味着ε-闭包最起码还是它本身。

如何求状态转换弧集?

理解状态转换弧集是什么？
假设状态集P是一个集合，那么P_a,p_b可以理解为，p输入a，b，之后会变成什么？将这个新变成的一个或多个元素，加入到一个新集合中。ε-闭包（新集合）就是状态转换弧集
注意点是：状态转换弧集不包含原先的弧集的，除非它可以指向自身循环
状态转换弧集没有p_ε这种情况，不要瞎求

看例题：

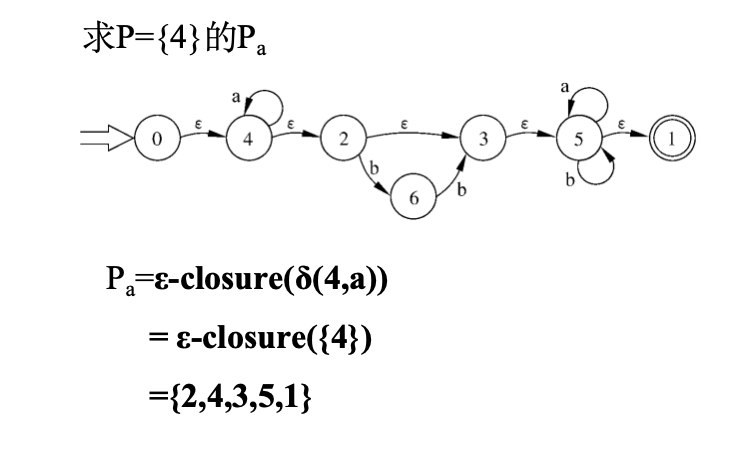
NFA转换为DFA的方法论

子集法NFA转换为DFA
解题步骤

1. 通过ε-闭包（开始状态）得到初始状态q₀
2. 对于每个状态，求它的状态转换弧集，如P_a,p_b这种，若产生新状态标记q₁ ，依此类推，重复步骤2，直到都完事，跳转步骤3
3. 确定结束状态，q集合中带有原先结束状态的集合，作为DFA的结束状态，要画两个圈
4. 根据前面得到的表格画图即可

真题实战

为了方便书写和查看，转换过程我们一般才用画表格的形式，更加直观，内部实现过程就是之前的一步一步，只不过在脑海中体现。

在做题的过程中，在熟练之后，要自然而然的在求出新集合后，直接加上它的ε-闭包。

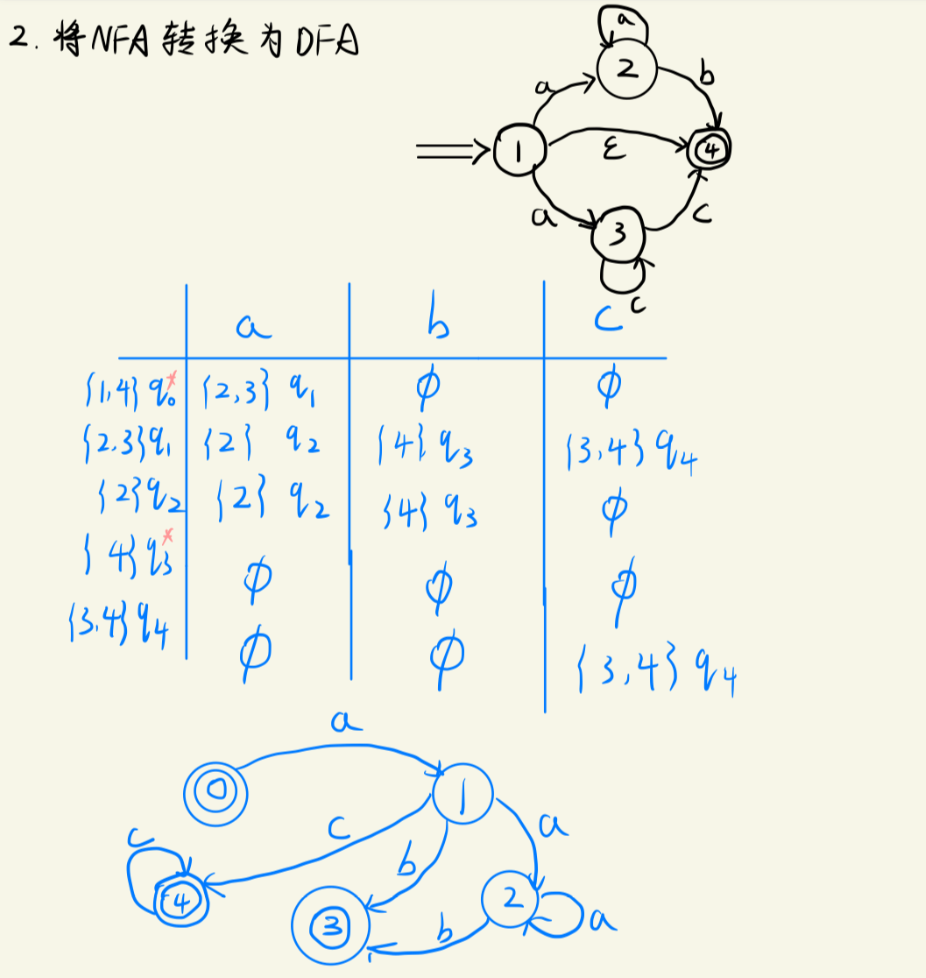
例题一

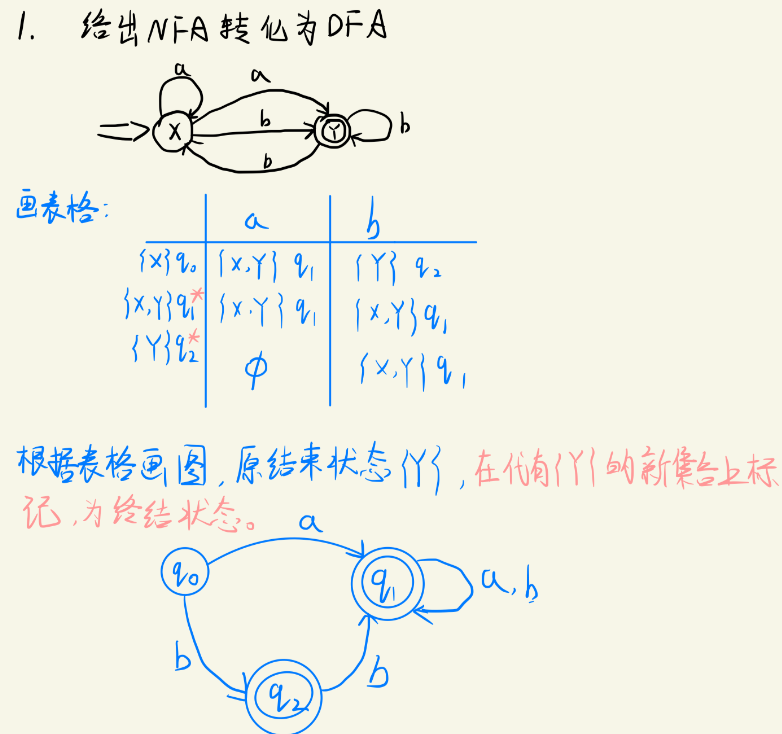
例题二