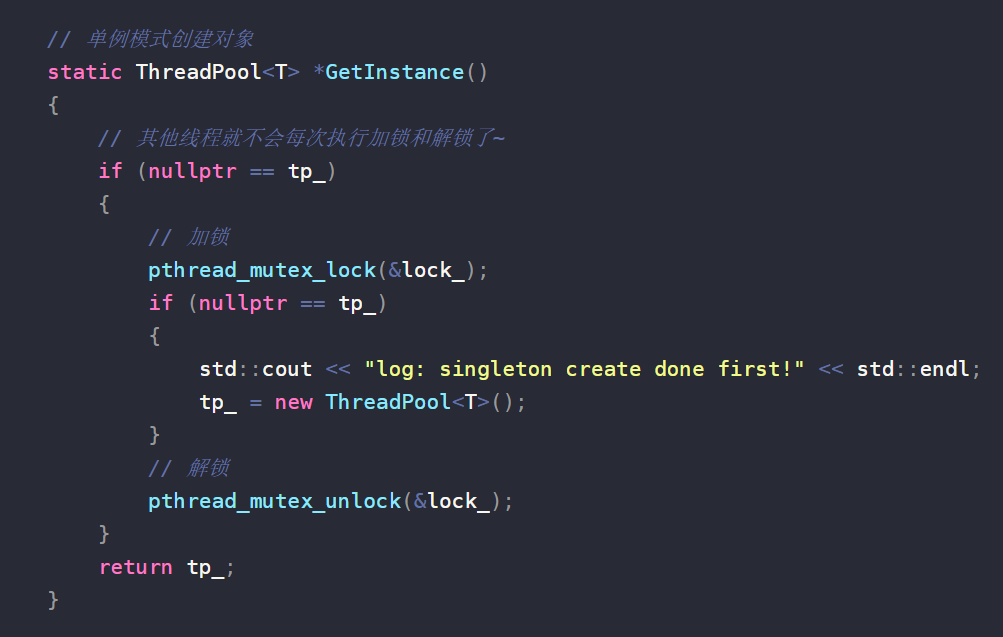
Good Morning, and in case I don't see you, good afternoon, good evening, and good night!
- 0. 一些概念
- 1. 坐标系的旋转
- 1.1 轴角法
- 1.2 四元素
- 1.3 基于欧拉角的旋转矩阵
- 1.3.1 单轴旋转矩阵
- 1.3.2 多轴旋转矩阵
- 1.3.3 其他
- 2. 齐次变换矩阵
- 3. visp实践
0. 一些概念
- 相关概念:旋转矩阵、平移矩阵、单应矩阵、齐次变换矩阵。
- 坐标变换包括旋转变换和平移变换。
- 为什么要坐标变换?引入坐标变换可以解决哪些问题?应用场景?
- 已知一点p在坐标系A中的坐标,计算p在坐标系B中的坐标。
- 已知一向量v在坐标系A中的值,计算v在坐标系B中的值。
- 描述坐标系A和坐标系B之间的位姿关系(姿态和位置)。
- 一向量v绕坐标系A的xyz轴旋转 θ ϕ ψ \theta \phi \psi θϕψ角度并进行一定平移后在坐标系A中的新坐标。
- 在数学建模过程中,往往需要将不同的物量量表示在同一个坐标系内才能列出等式。
- 刚体运动学。
- 图像的投影。
1. 坐标系的旋转
描述坐标系的旋转常用的方法包括:
- 轴角法
- 旋转矩阵
- 欧拉角
- 四元数
这几种旋转表示方法有各自的优缺点和应用场景,这里不作赘叙。
1.1 轴角法
不常用,略…
1.2 四元素
待续…
1.3 基于欧拉角的旋转矩阵
轴角法和四元数,这两个可以归纳为用一次旋转来表示两个坐标系间的姿态。欧拉角则是用三次旋转来表示姿态。

欧拉角指:横滚角
ϕ
\phi
ϕ,俯仰角
θ
\theta
θ,偏航角
ψ
\psi
ψ。
ϕ
,
θ
,
ψ
\phi, \theta, \psi
ϕ,θ,ψ在不同的领域有不同的定义规则:主要的区别是旋转顺序的不同,绕原始(固定)坐标轴轴旋转还是绕新(运动)坐标轴的不同(也称外旋或内旋)。
在航天航空领域的欧拉角:
- 内旋
绕运动轴旋转得到新坐标系。 - Z–>Y–>X
原始坐标系经过Z–>Y–>X顺序旋转一定的角度得到新坐标系。 - 右手系
涉及的坐标系都遵循右手定则。
1.3.1 单轴旋转矩阵
前提:右手系
这里只给出结论,不作推导。
坐标系A分别单独绕
x
,
y
,
z
x,y,z
x,y,z轴旋转
ϕ
,
θ
,
ψ
\phi, \theta, \psi
ϕ,θ,ψ角度,欧拉旋转矩阵表达式如下:
T
B
A
=
R
x
(
ϕ
)
=
[
1
0
0
0
c
o
s
ϕ
−
s
i
n
ϕ
0
s
i
n
ϕ
c
o
s
ϕ
]
(式
1
)
T
B
A
=
R
y
(
θ
)
=
[
c
o
s
θ
0
s
i
n
θ
0
1
0
−
s
i
n
θ
0
c
o
s
θ
]
(式
2
)
T
B
A
=
R
z
(
ψ
)
=
[
c
o
s
ψ
−
s
i
n
ψ
0
s
i
n
ψ
c
o
s
ψ
0
0
0
1
]
(式
3
)
T_B^A=R_x(\phi)= \begin{bmatrix} 1&0&0\\ 0&cos{\phi}&-sin{\phi}\\ 0&sin{\phi}&cos{\phi} \end{bmatrix}(式1)\\[3mm] T_B^A=R_y(\theta)= \begin{bmatrix} cos{\theta}&0&sin{\theta}\\ 0&1&0\\ -sin{\theta}&0&cos{\theta} \end{bmatrix}(式2)\\[3mm] T_B^A=R_z(\psi)= \begin{bmatrix} cos{\psi}&-sin{\psi}&0\\ sin{\psi}&cos{\psi}&0\\ 0&0&1 \end{bmatrix}(式3)
TBA=Rx(ϕ)=
1000cosϕsinϕ0−sinϕcosϕ
(式1)TBA=Ry(θ)=
cosθ0−sinθ010sinθ0cosθ
(式2)TBA=Rz(ψ)=
cosψsinψ0−sinψcosψ0001
(式3)
这些旋转矩阵的意义是:新坐标系到原始坐标系的变换矩阵,即:
[
x
A
y
A
z
A
]
=
T
B
A
[
x
B
y
B
z
B
]
\begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=T_B^A \begin{bmatrix} x_B\\ y_B\\ z_B \end{bmatrix}
xAyAzA
=TBA
xByBzB
注意:
- ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ满足右手定则,绕右手坐标系的正方向旋转时为正。
-
ϕ
,
θ
,
ψ
\phi, \theta, \psi
ϕ,θ,ψ是系A旋转运动到系B的旋转量,但是得到的旋转矩阵
R
x
,
R
y
,
R
z
R_x,R_y,R_z
Rx,Ry,Rz却是系B到系A的坐标变换矩阵!
即:
ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ:A ~> B
R x , R y , R z R_x,R_y,R_z Rx,Ry,Rz:B ~> A - 系B到系A的变换矩阵可以有多种符号表示方式,通常有:
T B A T_B^A TBA
A T B ^AT_B ATB
T A B T_{AB} TAB
都表示 B ~> A 的变换关系矩阵!注意上下标的位置!! - 旋转矩阵是正交的,因此有:
[ x B y B z B ] = T A B [ x A y A z A ] = ( T B A ) − 1 [ x A y A z A ] = ( T B A ) T [ x A y A z A ] \begin{bmatrix} x_B\\ y_B\\ z_B \end{bmatrix}=T_A^B \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=(T_B^A)^{-1} \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=(T_B^A)^{T} \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix} xByBzB =TAB xAyAzA =(TBA)−1 xAyAzA =(TBA)T xAyAzA
即: T A B = ( T B A ) − 1 = ( T B A ) T T_A^B=(T_B^A)^{-1}=(T_B^A)^{T} TAB=(TBA)−1=(TBA)T.
1.3.2 多轴旋转矩阵
12种常用的内旋欧拉角又可分为两个类别:
- 常规欧拉角
- 泰特 - 布赖恩角
注意: 下表中如
X
1
Y
2
Z
3
X_1Y_2Z_3
X1Y2Z3表示的是矩阵相乘顺序,相当于本文的
R
x
R
y
R
z
R_xR_yR_z
RxRyRz,表示旋转顺序是 Z ~>Y ~>X !其中的123表示绕该轴旋转的角度代称!

在航空航天领域,常用 Z ~>Y ~>X 旋转顺序的内旋欧拉角旋转矩阵。
例如,系A分别先后绕
Z
,
Y
,
X
Z,Y,X
Z,Y,X轴旋转
ψ
,
θ
,
ϕ
\psi,\theta,\phi
ψ,θ,ϕ角度,得到新的坐标系B,则有以下等式成立:
[
x
A
y
A
z
A
]
=
T
B
A
[
x
B
y
B
z
B
]
T
B
A
=
R
x
(
ϕ
)
R
y
(
θ
)
R
z
(
ψ
)
=
[
c
o
s
θ
c
o
s
ψ
−
c
o
s
θ
s
i
n
ψ
s
i
n
θ
c
o
s
ϕ
s
i
n
ψ
+
c
o
s
ψ
s
i
n
ϕ
s
i
n
θ
c
o
s
ϕ
c
o
s
ψ
−
s
i
n
ϕ
s
i
n
θ
s
i
n
ψ
−
c
o
s
θ
s
i
n
ϕ
s
i
n
ϕ
s
i
n
ψ
−
c
o
s
ϕ
c
o
s
ψ
s
i
n
θ
c
o
s
ψ
s
i
n
ϕ
+
c
o
s
ϕ
s
i
n
θ
s
i
n
ψ
c
o
s
ϕ
c
o
s
θ
]
(式
4
)
首旋:绕系
A
的
Z
轴旋转
ψ
角度
次旋:绕首旋得到的坐标系
A
′
的
Y
轴旋转
θ
角度
终旋:绕次旋得到的坐标系
A
′
′
的
X
轴旋转
ϕ
角度
系
A
→
首旋
→
系
A
′
→
次旋
→
系
A
′
′
→
终旋
→
系
B
\begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=T_B^A \begin{bmatrix} x_B\\ y_B\\ z_B \end{bmatrix} \\[5mm] T_B^A=R_x(\phi)R_y(\theta)R_z(\psi)=\begin{bmatrix} cos{\theta}cos{\psi}&-cos{\theta}sin{\psi}&sin{\theta}\\ cos{\phi}sin{\psi}+cos{\psi}sin{\phi}sin{\theta}&cos{\phi}cos{\psi}-sin{\phi}sin{\theta}sin{\psi}&-cos{\theta}sin{\phi}\\ sin{\phi}sin{\psi}-cos{\phi}cos{\psi}sin{\theta}&cos{\psi}sin{\phi}+cos{\phi}sin{\theta}sin{\psi}&cos{\phi}cos{\theta} \end{bmatrix}(式4)\\[5mm] 首旋:绕系A的Z轴旋转\psi角度\\[5mm] 次旋:绕首旋得到的坐标系A'的Y轴旋转\theta角度\\[5mm] 终旋:绕次旋得到的坐标系A''的X轴旋转\phi角度\\[5mm] 系A\to 首旋 \to 系A' \to 次旋 \to 系A'' \to 终旋 \to 系B
xAyAzA
=TBA
xByBzB
TBA=Rx(ϕ)Ry(θ)Rz(ψ)=
cosθcosψcosϕsinψ+cosψsinϕsinθsinϕsinψ−cosϕcosψsinθ−cosθsinψcosϕcosψ−sinϕsinθsinψcosψsinϕ+cosϕsinθsinψsinθ−cosθsinϕcosϕcosθ
(式4)首旋:绕系A的Z轴旋转ψ角度次旋:绕首旋得到的坐标系A′的Y轴旋转θ角度终旋:绕次旋得到的坐标系A′′的X轴旋转ϕ角度系A→首旋→系A′→次旋→系A′′→终旋→系B
旋转矩阵是正交的,因此有:
T
A
B
=
(
T
B
A
)
−
1
=
(
T
B
A
)
T
T_A^B=(T_B^A)^{-1}=(T_B^A)^{T}
TAB=(TBA)−1=(TBA)T
实质上,可以自行根据(式1)(式2)(式3)进行不同顺序的相乘,以得到特定的欧拉旋转矩阵,(式4)就是下面相乘顺序得到的结果:
T
B
A
=
R
x
(
ϕ
)
R
y
(
θ
)
R
z
(
ψ
)
T_B^A=R_x(\phi)R_y(\theta)R_z(\psi)
TBA=Rx(ϕ)Ry(θ)Rz(ψ)
注意,越靠右边旋转顺序越优先!!
1.3.3 其他
- 优点:简洁直观。
- 缺点:万向节死锁,意思是在某些姿态下,欧拉角的三自由度失去了一个自由度。
- 扩展结论:
- 欧拉角旋转矩阵是正交的,有 R T = R − 1 R^T=R^{-1} RT=R−1
- 三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动轴旋转的最终姿态相同。
- 欧拉角+旋转矩阵才能 VS 轴角法+四元数
- 外旋欧拉旋转矩阵请自行查阅其他资料。
2. 齐次变换矩阵
将两个坐标系的旋转关系和平移关系整合成一个4x4的矩阵。
[
x
b
y
b
z
b
1
]
=
b
T
a
[
x
a
y
a
z
a
1
]
=
[
b
R
a
O
a
b
0
1
]
[
x
a
y
a
z
a
1
]
\begin{bmatrix} x_b \\ y_b \\ z_b \\ 1 \end{bmatrix}={^bT_a} \begin{bmatrix} x_a \\ y_a \\ z_a \\ 1 \end{bmatrix}= \begin{bmatrix} ^bR_a&O_a^b \\ 0&1 \\ \end{bmatrix} \begin{bmatrix} x_a \\ y_a \\ z_a \\ 1 \end{bmatrix}
xbybzb1
=bTa
xayaza1
=[bRa0Oab1]
xayaza1
b
T
a
=
[
b
R
a
O
a
b
0
1
]
{^bT_a} = \begin{bmatrix} ^bR_a&O_a^b \\ 0&1 \\ \end{bmatrix}
bTa=[bRa0Oab1]
其中:
b
T
a
^bT_a
bTa称为坐标系 a 到坐标系 b 的齐次变换矩阵;
b
R
a
^bR_a
bRa是系a到系b的旋转矩阵;
O
a
b
O_a^b
Oab是系a原点在系b中的坐标;
坐标系 a 到坐标系 b 的齐次变换矩阵为
b
T
a
^bT_a
bTa,那么坐标系 b 到坐标系 a 的齐次变换矩阵为
a
T
b
=
(
b
T
a
)
−
1
^aT_b=(^bT_a)^{-1}
aTb=(bTa)−1,根据齐次矩阵的性质,可知:
a
T
b
=
(
b
T
a
)
−
1
=
[
a
R
b
−
a
R
b
O
a
b
0
1
]
^aT_b=(^bT_a)^{-1}= \begin{bmatrix} ^aR_b&-^aR_bO_a^b \\ 0&1 \\ \end{bmatrix}
aTb=(bTa)−1=[aRb0−aRbOab1]
3. visp实践
待续…
vpRxyzVector c1_rxyz_c(vpMath::rad(0.0), vpMath::rad(90), 0);//vpMath::rad(-10.0), vpMath::rad(0), 0
vpRotationMatrix c1Rc(c1_rxyz_c); // 旋转矩阵:c1 -> c
vpHomogeneousMatrix c1Mc(vpTranslationVector(), c1Rc); // 齐次变换矩阵:c1 -> c
vpRotationMatrix c1Re { 1, 0, 0, 0, 0, 1, 0, -1, 0 }; // 旋转矩阵:e -> c1
vpTranslationVector c1te(0, 0, 0); // 平移关系:e -> c1 0, -0.03, -0.07
vpHomogeneousMatrix c1Me(c1te, c1Re); // 齐次变换矩阵:e -> c1
vpHomogeneousMatrix cMe = c1Mc.inverse() * c1Me; // Homogeneous matrix between (c) and (e) //c与e的单应矩阵
vpVelocityTwistMatrix cVe(cMe); //齐次变换矩阵:e -> c
std::cout << "c1Mc: " << c1Mc << std::endl;
std::cout << "c1Mc.inverse(): " << c1Mc.inverse() << std::endl;
std::cout << "c1Mc.inverse()*c1Mc: " << c1Mc.inverse()*c1Mc << std::endl;
std::cout << "cMe: " << cMe << std::endl;
std::cout << "c1Me: " << c1Me << std::endl;
std::cout << "cVe: " << cVe << std::endl;
std::cout << "c1Re: " << c1Re << std::endl;
std::cout << "c1Rc: " << c1Rc << std::endl;
std::cout << "c1_rxyz_c: " << c1_rxyz_c << std::endl;
c1Mc:
0 0 1 0
0 1 0 0
-1 0 0 0
0 0 0 1
c1Mc.inverse():
0 0 -1 0
0 1 0 0
1 0 0 0
0 0 0 1
c1Mc.inverse()*c1Mc:
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
cMe:
0 1 0 0
0 0 1 0
1 0 0 0
0 0 0 1
c1Me:
1 0 0 0
0 0 1 0
0 -1 0 0
0 0 0 1
cVe:
0 1 0 0 0 0
0 0 1 0 0 0
1 0 0 0 0 0
0 0 0 0 1 0
0 0 0 0 0 1
0 0 0 1 0 0
c1Re:
1 0 0
0 0 1
0 -1 0
c1Rc:
0 0 1
0 1 0
-1 0 0
c1_rxyz_c:
0
1.570796327
0





![[OtterCTF 2018]Name Game](https://img-blog.csdnimg.cn/img_convert/03a980ee574bf77b4820474ccf280107.png)