第三章.逻辑回归
3.1 逻辑回归(Logistic Regression)
线性回归以及非线性回归是用来处理回归问题的,而逻辑回归是用来处理分类问题的。
1.应用场景:
1).分类:
- 垃圾邮件分类
- 预测肿瘤是良性还是恶行
- 预测某人的信用是好是坏
2.Sigmoid / Logistic Function
1).Sigmoid/Logistic函数:
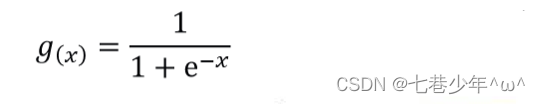
2).预测函数:
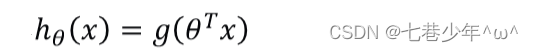
- 将g(x)代到h0(x)中:
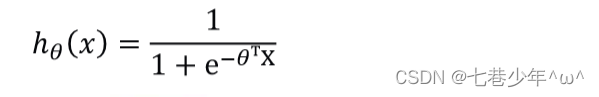
3).图像:
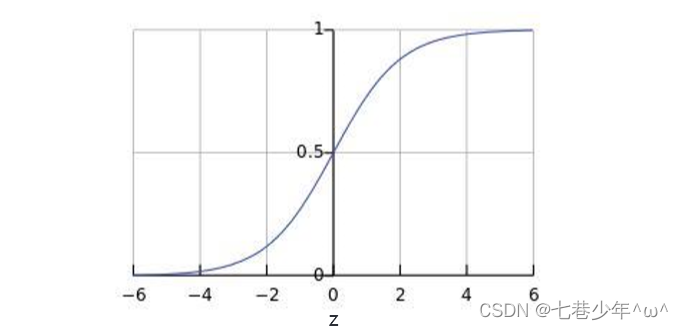
- 图像描述:
①.0.5可以作为分类的边界
②.当z≥0时,g(z)≥0.5;当θTX≥0时,g(θTX)≥0.5
③.当z≤0时,g(z)≤0.5;当θTX≤0时,g(θTX)≤0.5
3.决策边界
1).
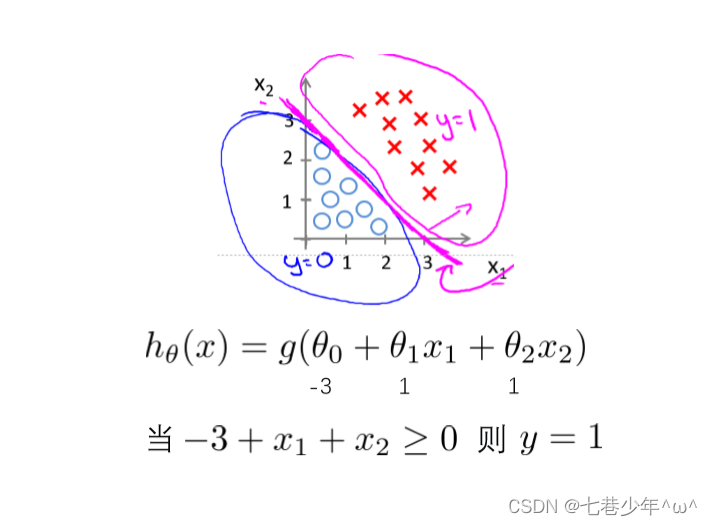
- 图像描述:
①.线下面的点都是小于0的,属于标签为0的类别
②.线上面的点都是大于0的,属于标签为1的类别
2).

- 图像描述:
①.圈内点都是小于0的,属于标签为0的类别
②.圈外的点都是大于0的,属于标签为1的类别
3).
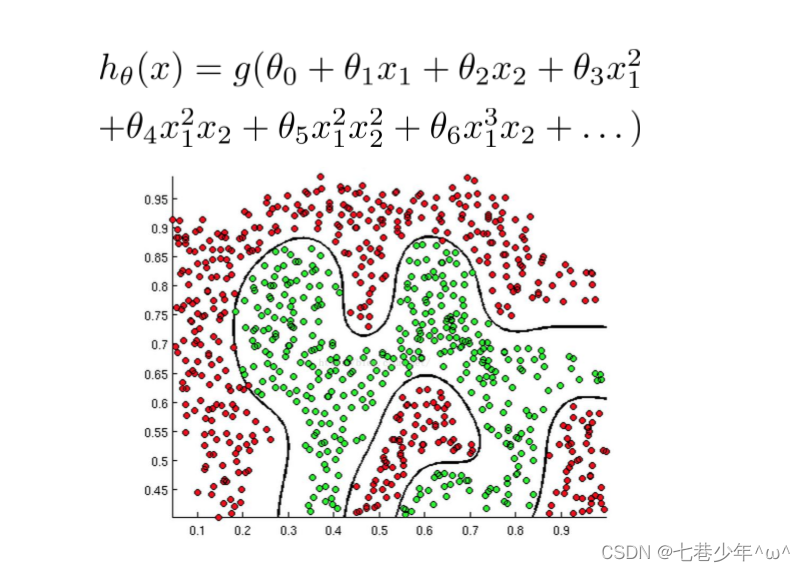
- 图像描述:
①.决策边界内的点都是小于0的,属于标签为0的类别
②.决策边界外的点都是大于0的,属于标签为1的类别
4.逻辑回归的代价函数
1).图像:
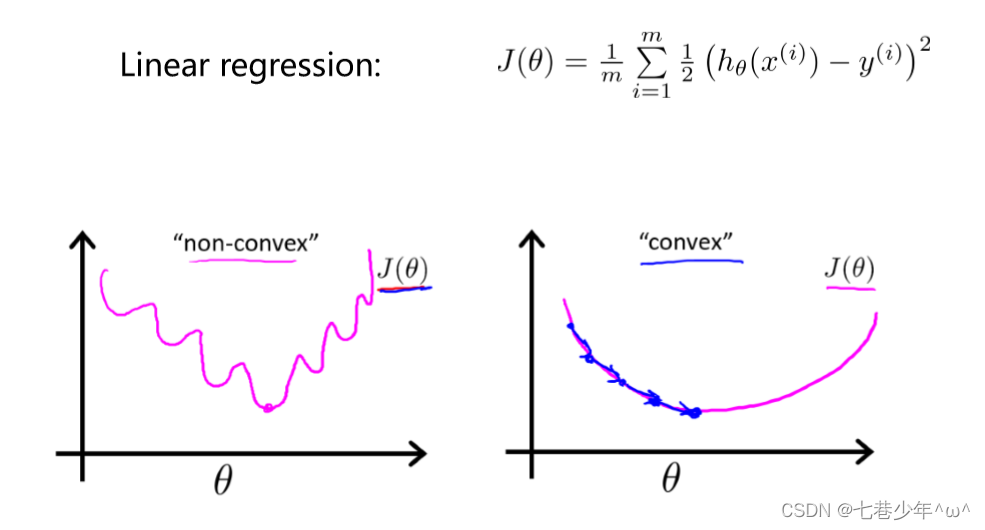
- 说明:非凸函数在使用线性回归的代价函数的梯度下降法的时候,会存在多个局部极小值,不利于参数的求解,因此引入了逻辑回归的代价函数。
2).代价函数
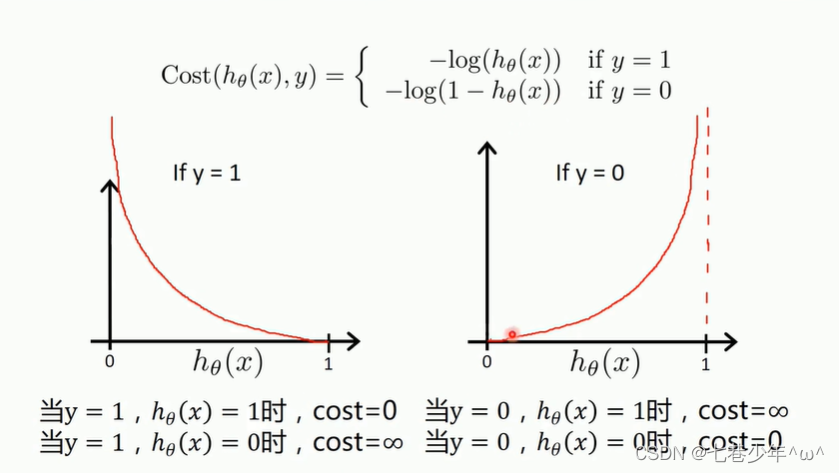
- 参数说明:
①.h0(x):预测值
②.y:样本标签
3).转换:
①.两个公式合并成一个公式: (深度学习中交叉熵也是这个公式)
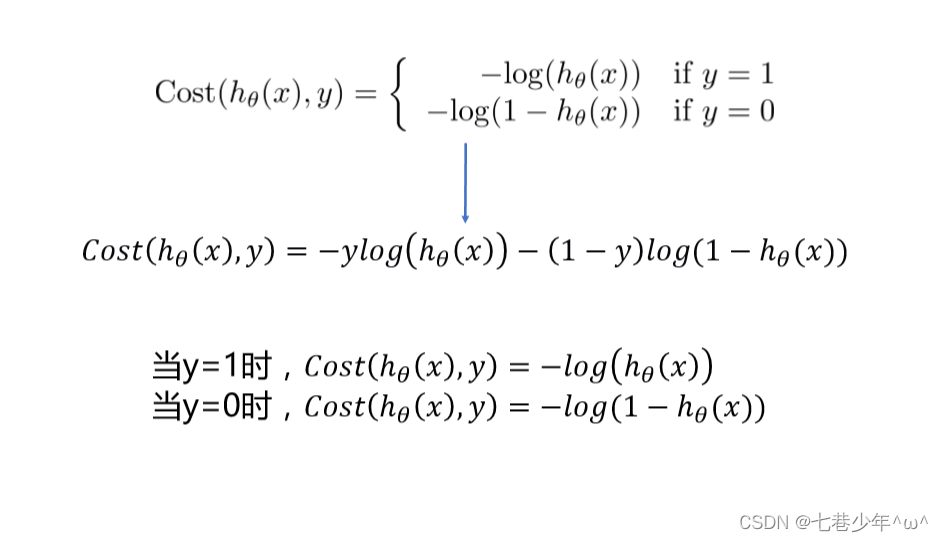
②.梯度下降法求解逻辑回归:

③.求导的过程:

- 涉及到的公式:
| 公式 |
|---|
| ( logax)'=1/xlna |
| (θT x) ’ = x |
| lne=1 |
| log是以e为底 |
④.最终的公式:

5.多分类
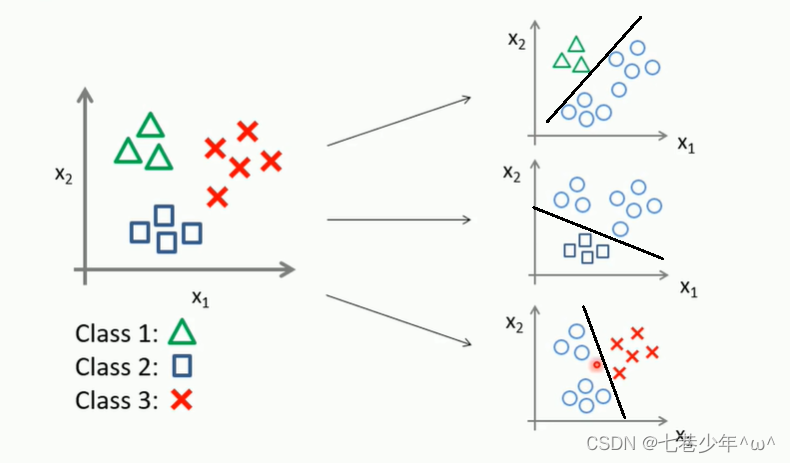
- 图像描述:
①.多分类可以做多个决策边界
6.逻辑回归正则化
1).普通逻辑回归代价函数:
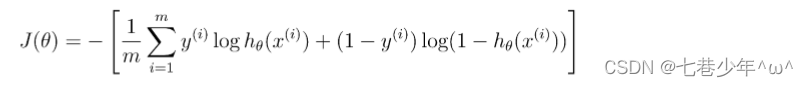
2).正则化逻辑回归代价函数:
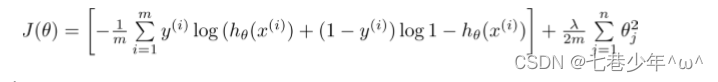
3).求导:
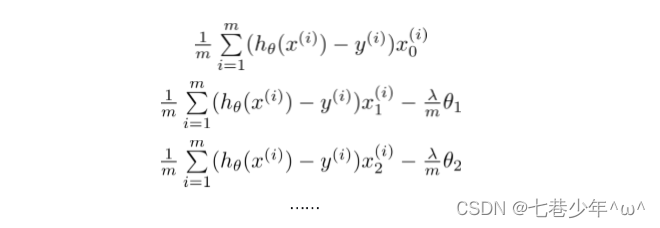
7.实战1:梯度下降法—逻辑回归:
数据标准化有利于优化梯度下降法。
1).CSV中的数据:
- LR-testSet.csv
2).代码
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
# 数据是否需要标准化
scale = False
# 载入数据
data = np.genfromtxt('D:\\Data\\LR-testSet.csv', delimiter=',')
# 数据切片
x_data = data[:, :-1]
y_data = data[:, -1]
# 画图
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
# 切分不同类别的数据:区分标签0和标签1
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i, 0])
y0.append(x_data[i, 1])
else:
x1.append(x_data[i, 0])
y1.append(x_data[i, 1])
# 画散点图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
# 图例
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
plot()
plt.show()
# 数据处理
# 增加维度
y_data = data[:, -1, np.newaxis]
# 给样本增加偏置项
X_data = np.concatenate((np.ones((100, 1)), x_data), axis=1)
lr = 0.001
epochs = 10000
costList = []
# sigmoid函数
def sigmoid(x):
return 1.0 / (1 + np.exp(-x))
# 代价函数
def cost(xMat, yMat, ws):
value1 = np.multiply(yMat, np.log(sigmoid(xMat * ws)))
value2 = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat * ws)))
return np.sum(value1 + value2) / - (len(xMat))
# 梯度下降函数
def gradAscent(xArr, yArr):
# 判断数据是否需要标准化
if scale == True:
xArr = preprocessing.scale(xArr)
xMat = np.mat(xArr)
yMat = np.mat(yArr)
# 返回数据的行列数
m, n = np.shape(xMat)
# 初始化权值
ws = np.mat(np.ones((n, 1)))
for i in range(epochs + 1):#+1是为了记录最后一次的代价函数的值
h = sigmoid(xMat * ws)
# 计算误差
# xMat使用转置的原因:xMat是[100,3],转置后[3,100],h是[100,1],ws_grad是[3,1],回归参数正好是[3,1]的
ws_grad = xMat.T * (h - yMat) / m
ws = ws - lr * ws_grad
if i % 50 == 0:
costList.append(cost(xMat, yMat, ws))
return ws, costList
# 训练模型,得到权重和cost值得变化
ws, costList = gradAscent(X_data, y_data)
if scale == False:
# 绘制决策边界
plot()
x_test = [[-4], [3]]
#y_test公式的由来:直线方程:w0+w1*x+w2*y=0 -> y=(-w0-w1*x)/w2
y_test = (-ws[0] - x_test * ws[1]) / ws[2]
plt.plot(x_test, y_test, 'k')
plt.show()
# 绘制loss值得变化
x = np.linspace(0, 10000, 201)#每50次记录一下,一共记录了201次
plt.plot(x, costList, c='r')
plt.title('Train')
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.show()
# 预测
def predict(x_data, ws):
if scale == True:
x_data = preprocessing.scale(x_data)
xMat = np.mat(x_data)
ws = np.mat(ws)
return [1 if x >= 0.5 else 0 for x in sigmoid(xMat * ws)]
precisions = predict(X_data, ws)
print(classification_report(y_data, precisions))
3).结果展示:
①.数据
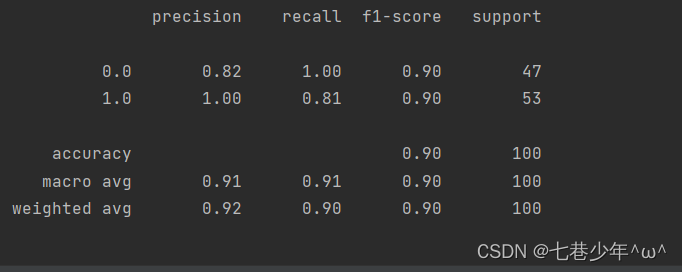
②.图像
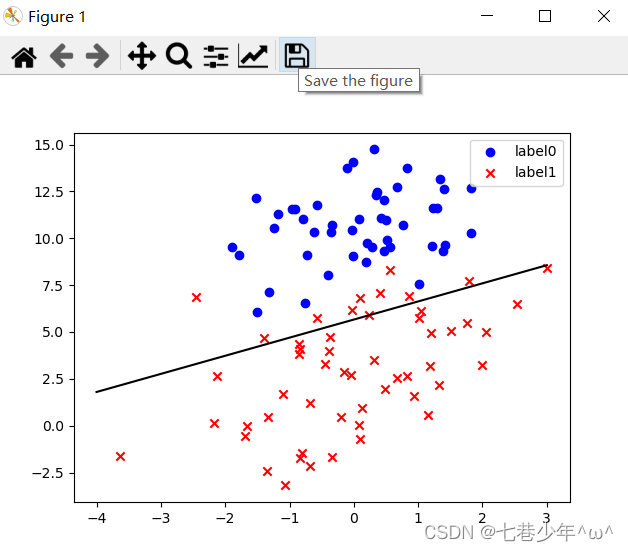
8.实战2: sklearn—逻辑回归:
数据标准化有利于优化梯度下降法。
1).CSV中的数据:
- LR-testSet.csv
2).代码
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from sklearn.metrics import classification_report
# 数据是否需要标准化
scale = False
# 载入数据
data = np.genfromtxt('D:\\Data\\LR-testSet.csv', delimiter=',')
x_data = data[:, :-1]
y_data = data[:, -1]
# 画图
def plot():
x0 = []
y0 = []
x1 = []
y1 = []
# 切分不同类别的数据
for i in range(len(x_data)):
if (y_data[i] == 0):
x0.append(x_data[i, 0])
y0.append(x_data[i, 1])
else:
x1.append(x_data[i, 0])
y1.append(x_data[i, 1])
# 绘制散斑点
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
# 绘制图例
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'])
plot()
plt.show()
# 创建并拟合模型
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
# 截距
intercept = logistic.intercept_
# 回归系数
coef = logistic.coef_
if scale == False:
# 绘制决策边界
plot()
x_test = np.array([[-4], [3]])
y_test = (-intercept - x_test * coef[0][0]) / coef[0][1]
plt.plot(x_test, y_test, 'k')
plt.show()
# 预测值
predictions = logistic.predict(x_data)
print(classification_report(y_data, predictions))
3).结果展示:
①.数据
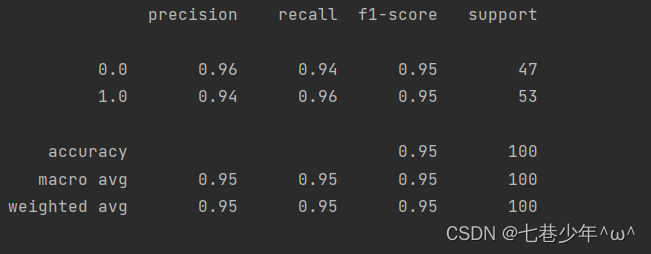
②.图像