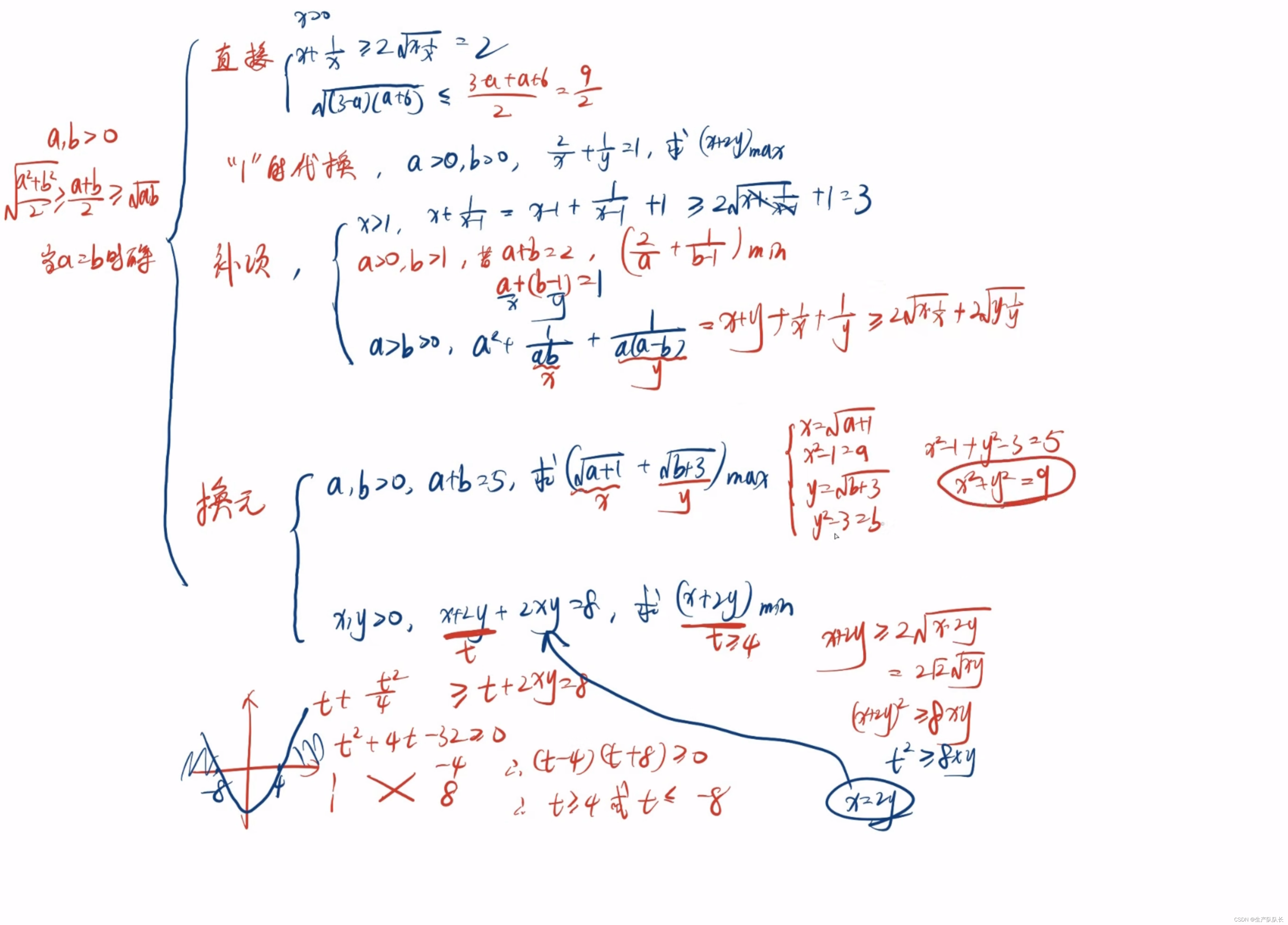
一、“1”的代换
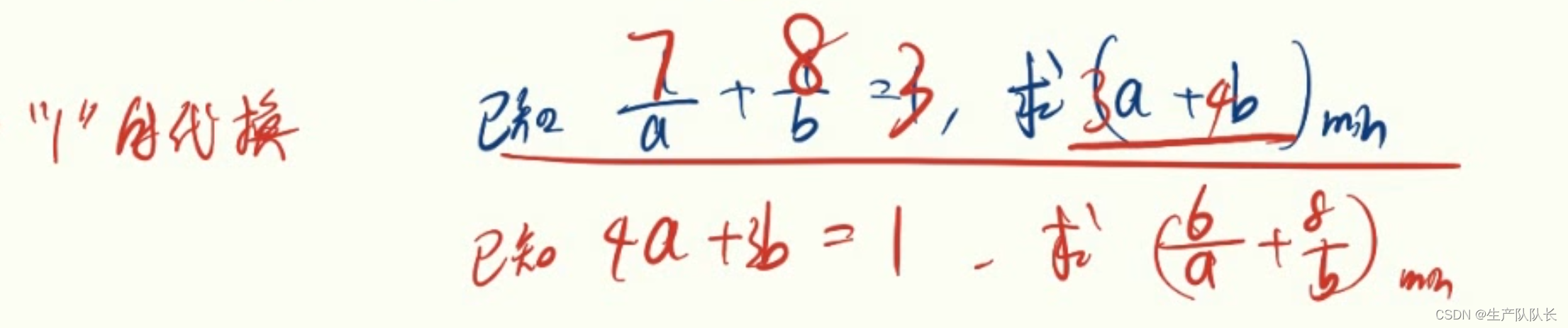
练习
例题1

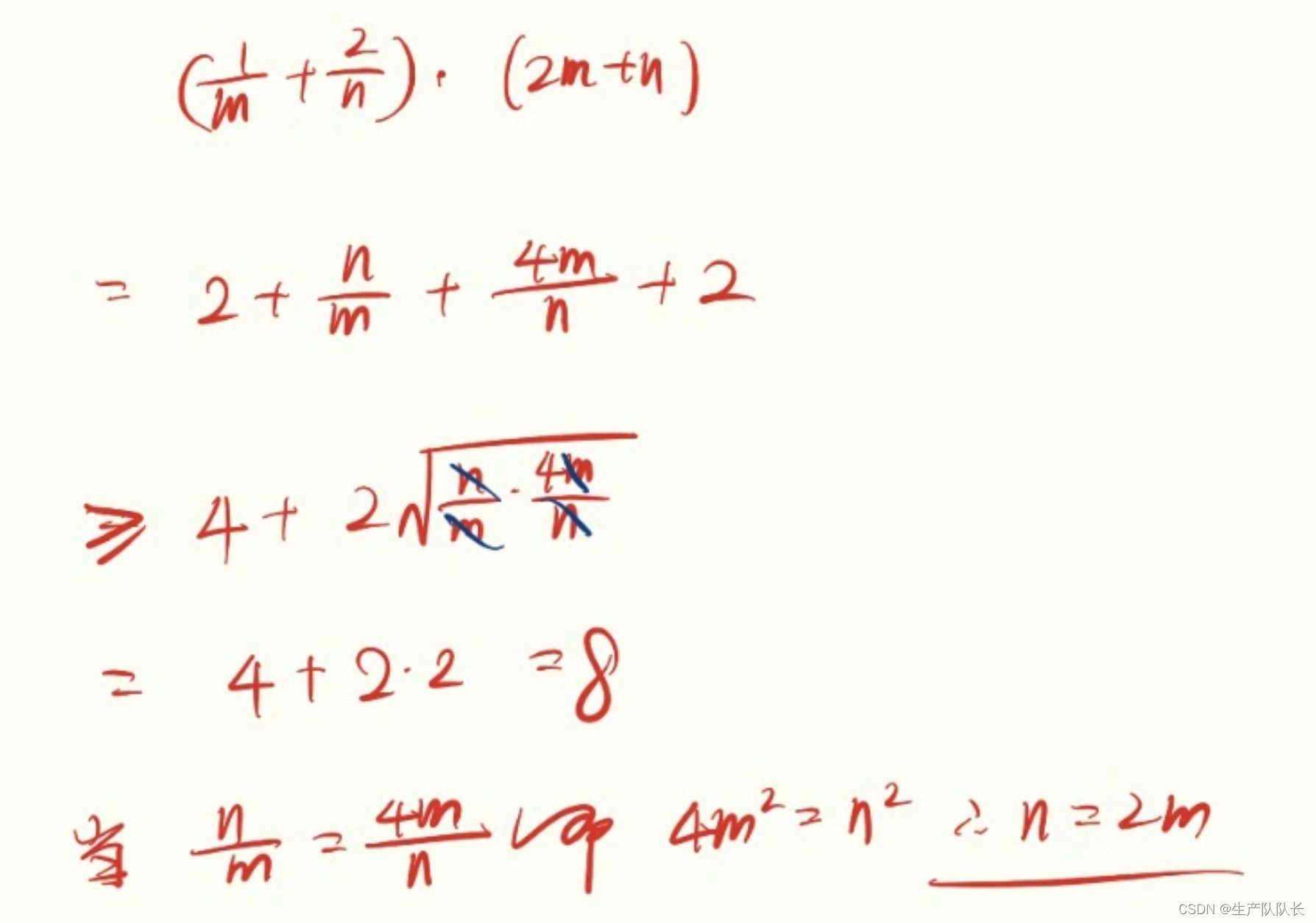
例题2

解


二、基本不等式中的“变形”
就是,一般情况下,我们在题目中,是不能够直接使用基本不等式进行求解的。
而是要对条件等式进行变形,满足基本不等式的使用条件
练习
例题1
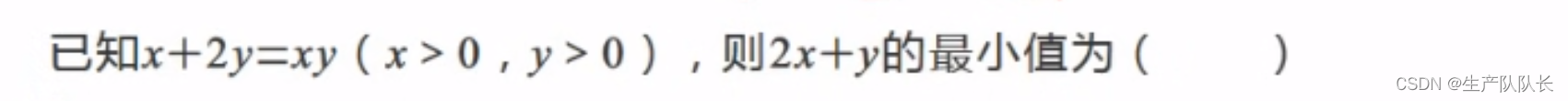
解析
两边同时乘以
1
x
y
\frac{1}{xy}
xy1,这样,题目就转化成了:“1”的代换。
例题2

解析
因为
x
>
1
,
所以,
x
−
1
>
0
x>1,所以,x-1>0
x>1,所以,x−1>0
y
=
2
x
+
2
x
−
1
⇒
y
=
2
(
x
−
1
)
+
2
(
x
−
1
)
+
2
y=2x+\frac{2}{x-1} \Rightarrow y=2(x-1)+\frac{2}{(x-1)} + 2
y=2x+x−12⇒y=2(x−1)+(x−1)2+2
最后,记得求出取等条件时,x的值。
例题3

解:
第一问(较难)
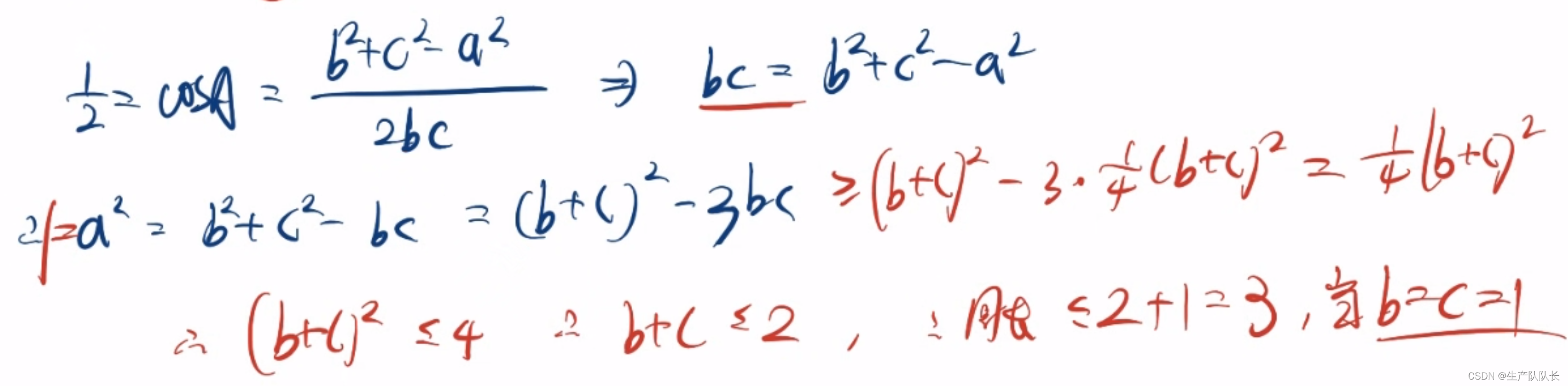
第二问
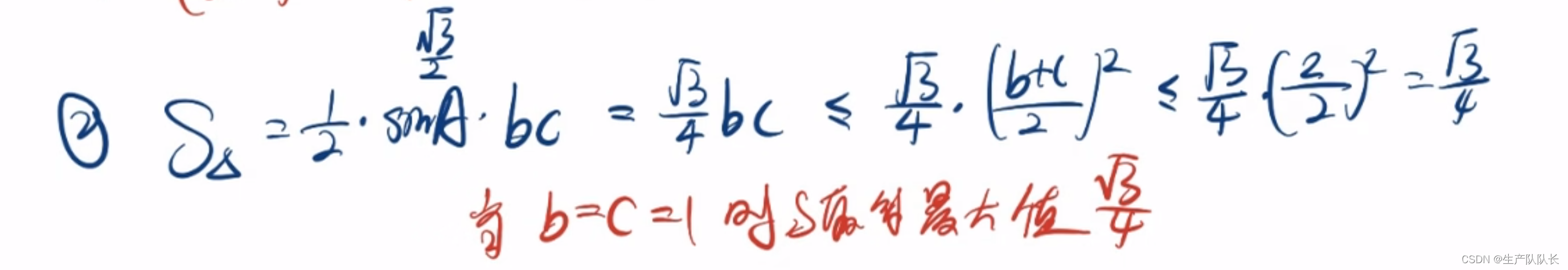
三、线性规划
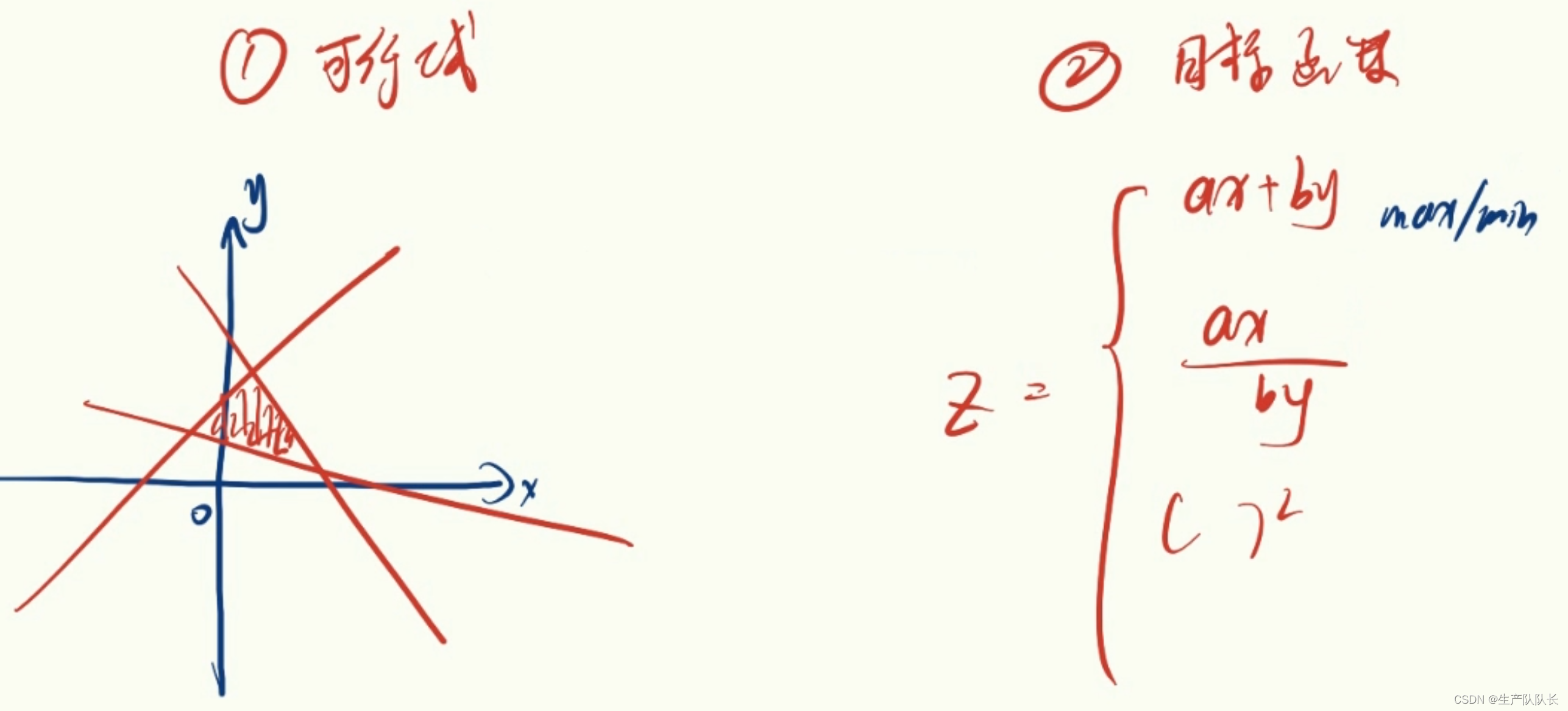
解题步骤
1、画出可行域
2、将目标函数的斜率与条件函数的斜率比较
3、在可行域内移动目标函数,得出最优解
练习
例题1

解
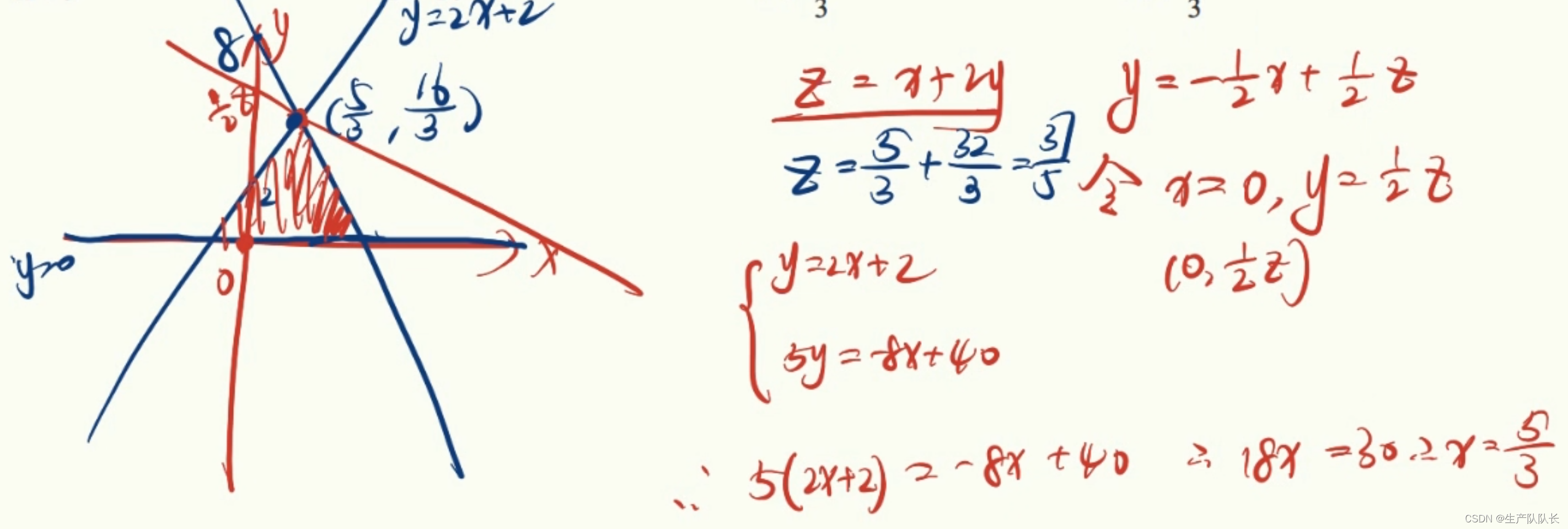
例题2

解
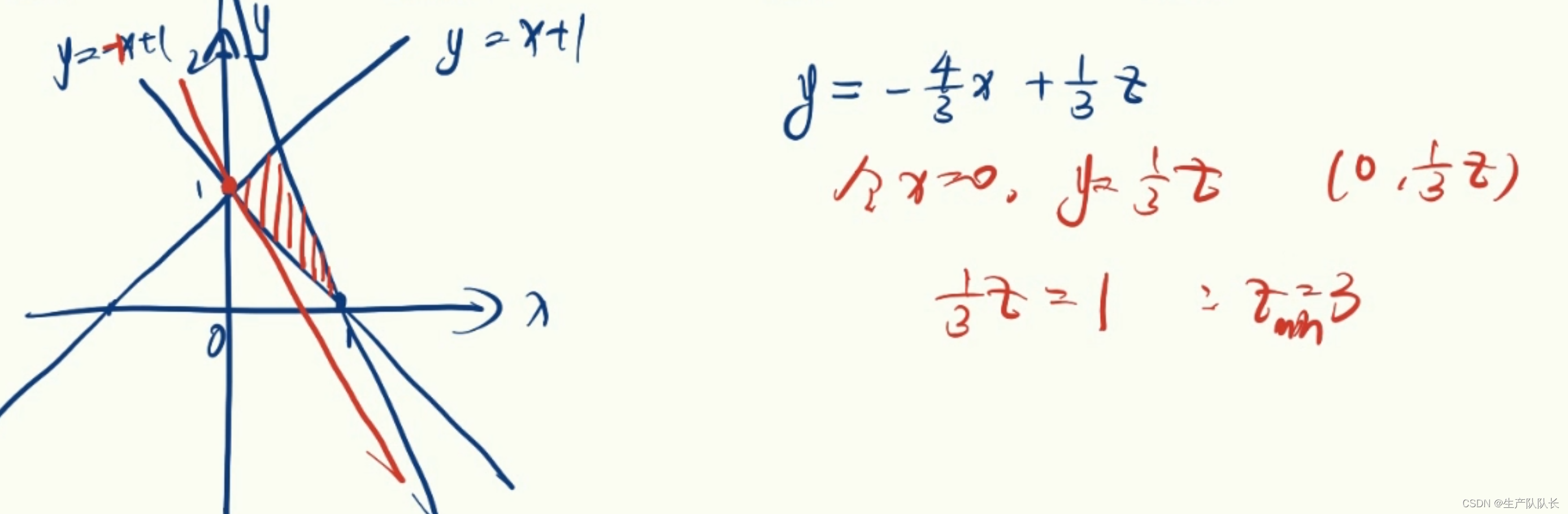
例题3

解
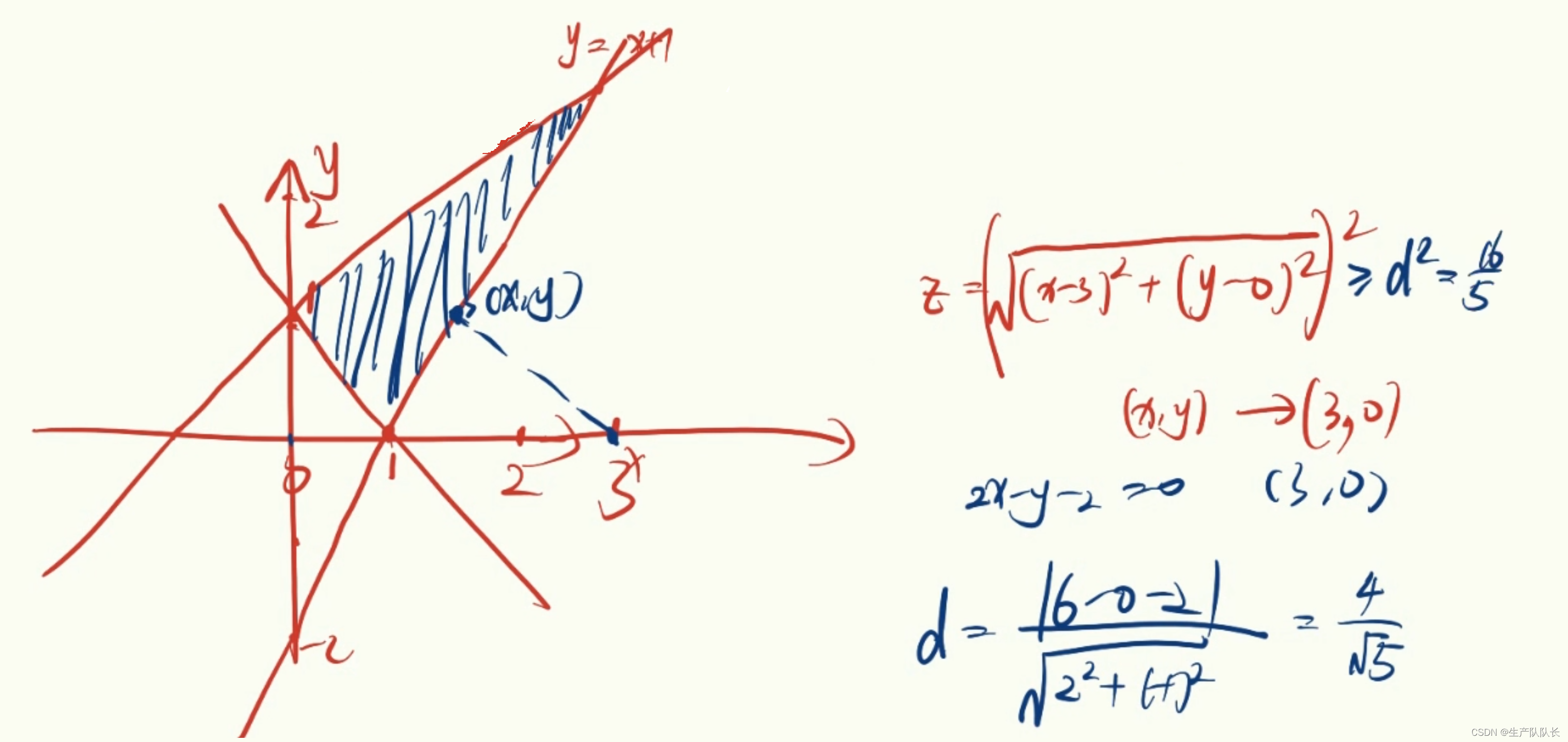
我们可以看出,根据目标函数的不同,最值的几何特点也不同。
1,2两题就是找y轴的截距最值。
第3题,转化成了点到直线距离的最值问题。
四、总结