简介
物理信息神经网络(Physic informed neural network,PINN)已经成为在有限差分、有限体积和有限元之后的另一种求解偏微分方程组的范式,受到学者们广泛关注。
在固体力学领域有两类不同的PINN:
(1)PDE-based method: 第一类使用神经网络表示位移场,将控制方程的残差直接引入神经网络的损失函数,通过梯度下降算法优化神经网络的权重和偏置,最终使得方程残差最小
(2)Energy-based method: 第二类使用神经网络表示位移场,将结构的总势能引入神经网络的损失函数,通过梯度下降算法优化神经网络的权重和偏置,最终使得结构的总势能最小。这种方法又被称为“深度里兹法”1,体现的是最小势能原理,可以参见变分原理与泛函分析教程。
二者在理论上是等价的,但是Energy-based方法在数学上更加直接,所以这里重点介绍第二类方法。
神经网络
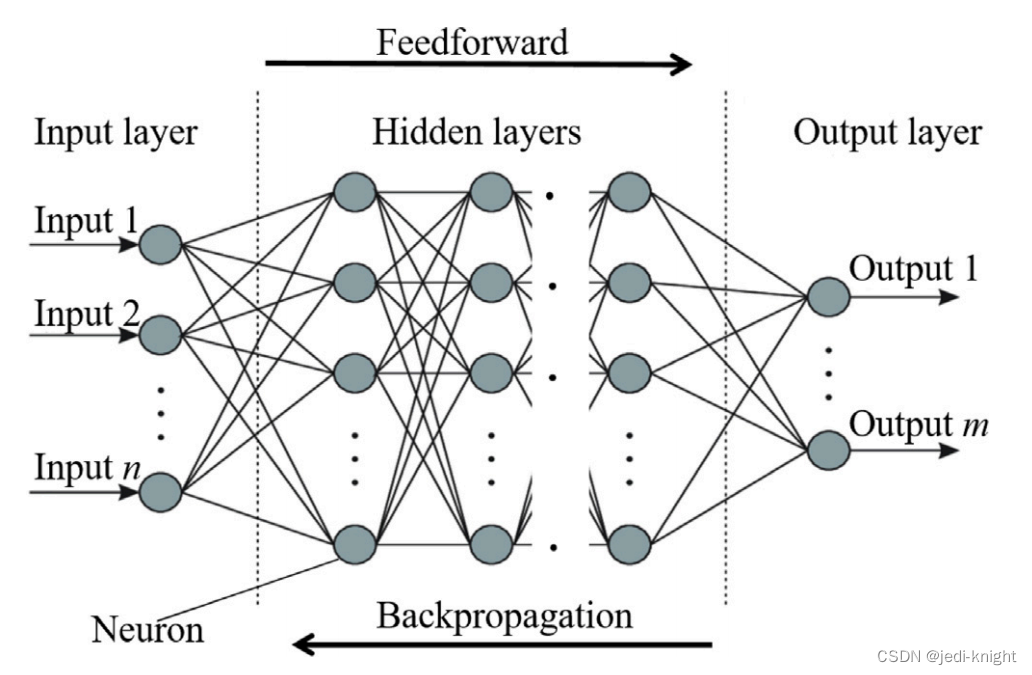
PINN的神经网络通常都十分简单,输入空间坐标,经过隐藏层后,输出位移场。对于二维问题则输出两个量,对于三维问题则输出三个量。之所以要使用神经网络来表示解,是因为:
(1)神经网络是可微分的,使用自动求导机制可以精确地获得输出对输入的偏导数
(2)神经网络可以逼近任意复杂的连续函数。
 位移边界条件的定义方式可参见2
位移边界条件的定义方式可参见2
u
^
(
X
,
ϕ
)
=
A
(
X
)
+
B
(
X
)
∘
y
^
(
X
,
ϕ
)
\hat{\boldsymbol{u}}(\boldsymbol{X}, \boldsymbol{\phi})=\boldsymbol{A}(\boldsymbol{X})+\boldsymbol{B}(\boldsymbol{X}) \circ \hat{\boldsymbol{y}}(\boldsymbol{X}, \boldsymbol{\phi})
u^(X,ϕ)=A(X)+B(X)∘y^(X,ϕ)
B
(
X
)
B(X)
B(X)为距离函数,当
X
X
X落在位移边界条件上时,
B
B
B为0。
A
(
X
)
A(X)
A(X)表示边界上的位移分布
应力边界条件以外力虚功的形式引入损失函数
损失函数为总势能,如下
L
=
∫
Ω
ψ
^
(
X
,
ϕ
)
d
Ω
−
∫
Γ
u
^
T
(
X
,
ϕ
)
t
‾
d
Γ
\mathcal{L}=\int_{\Omega} \hat{\psi}(\boldsymbol{X}, \boldsymbol{\phi}) d \Omega-\int_{\Gamma} \hat{\boldsymbol{u}}^{T}(\boldsymbol{X}, \boldsymbol{\phi}) \overline{\boldsymbol{t}} d \Gamma
L=∫Ωψ^(X,ϕ)dΩ−∫Γu^T(X,ϕ)tdΓ第一项为整个体系的应变能,第二项为外力虚功对应的势能。特别地,如果只有位移边界条件而不存在应力边界条件,那么边界上的功为0.
损失函数达到最小即系统处于最小势能状态。此时,任意虚位移下,总势能都不变,内力虚功与外力虚功之和为0,系统处于平衡状态。
对于不同的材料(线弹性材料、超弹性材料、黏弹性材料),应变能密度 ψ ^ \hat{\psi} ψ^的表达式都是不同的,列于下方,具体含义见3。
线弹性材料
ψ
=
1
2
ε
i
j
σ
i
j
\psi=\frac{1}{2} \varepsilon_{i j} \sigma_{i j}
ψ=21εijσij
应力由应变得到
σ
=
λ
trace
(
ε
)
I
+
2
μ
ε
\boldsymbol{\sigma}=\lambda \operatorname{trace}(\varepsilon) \boldsymbol{I}+2 \mu \boldsymbol{\varepsilon}
σ=λtrace(ε)I+2με应变由位移得到
ε
=
1
2
(
∇
u
+
∇
u
T
)
\boldsymbol{\varepsilon}=\frac{1}{2}\left(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{T}\right)
ε=21(∇u+∇uT)
超弹性材料
ψ
=
∑
r
=
1
M
3
1
−
α
r
2
α
r
μ
r
(
I
1
α
r
−
3
α
r
)
−
∑
r
=
1
M
μ
r
ln
J
+
λ
2
(
J
−
1
)
2
\psi=\sum_{r=1}^{M} \frac{3^{1-\alpha_{r}}}{2 \alpha_{r}} \mu_{r}\left(I_{1}^{\alpha_{r}}-3^{\alpha_{r}}\right)-\sum_{r=1}^{M} \mu_{r} \ln J+\frac{\lambda}{2}(J-1)^{2}
ψ=r=1∑M2αr31−αrμr(I1αr−3αr)−r=1∑MμrlnJ+2λ(J−1)2
第一不变量
I
1
I_1
I1、行列式
J
J
J等由变形梯度张量
F
\boldsymbol{F}
F确定
黏弹性材料
ψ
=
[
1
2
ε
i
j
L
i
j
k
l
0
ε
k
l
+
1
2
(
ε
i
j
−
ε
i
j
v
)
L
i
j
k
l
1
(
ε
k
l
−
ε
k
l
v
)
]
+
[
Δ
t
1
2
ε
˙
i
j
v
M
i
j
k
l
ε
˙
k
l
v
]
\psi = \left[ {{1 \over 2}{\varepsilon _{ij}}L_{ijkl}^0{\varepsilon _{kl}} + {1 \over 2}\left( {{\varepsilon _{ij}} - \varepsilon _{ij}^v} \right)L_{ijkl}^1\left( {{\varepsilon _{kl}} - \varepsilon _{kl}^v} \right)} \right] + \left[ {\Delta t{1 \over 2}\dot \varepsilon _{ij}^vM_{ijkl}^{}\dot \varepsilon _{kl}^v} \right]
ψ=[21εijLijkl0εkl+21(εij−εijv)Lijkl1(εkl−εklv)]+[Δt21ε˙ijvMijklε˙klv]
注意,第二项中含有时间
E W., Yu B. The Deep Ritz Method: A Deep Learning-Based Numerical Algorithm for Solving Variational Problems[J]. Communications in Mathematics and Statistics, 2018, 6(1): 1-12 ↩︎
Rao C., Sun H., Liu Y. Physics-Informed Deep Learning for Computational Elastodynamics without Labeled Data[J]. Journal of Engineering Mechanics, 2021, 147(8): 4021043 ↩︎
Abueidda D.W., Koric S., Guleryuz E., et al. Enhanced physics-informed neural networks for hyperelasticity[J]. International Journal for Numerical Methods in Engineering, 2023, 124(7): 1585-1601 ↩︎