假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

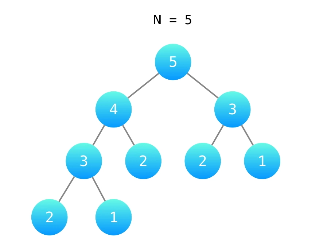
通过规律观察发现：

楼顶数：1        2        3        4        5        6

方法数：1        2        3        5        8        13

1.递归

int F(int n)
{
    if(n<=2)
        return n;
    else
        return F(n-1)+F(n-2);
}

2.记忆递归

int arr[46]={0};
F(int n)
{
    if(n<=2)
        return n;
    if(arr[n]!=0)
        return arr[n];
    else
        return arr[n]=F(n-1)+F(n-2);
}

3.动态规划（减少了递归带来的内存申请）

int F(int n){
    int arr[46]={0};
    arr[1]=1,arr[2]=2;
    for(int i=3;i<n+1;i++)
    {
        arr[i]=arr[i-1]+arr[i-2];
    }
    return arr[n];
}

4.滚动数组

int F(int n) {
    int a = 0, b = 0, r = 1;
    for (int i = 1; i <= n; ++i) {
        a = b;
        b = r;
        r = a + b;
    }
    return r;
}