1.前言

（1）虽然我学习这个数学建模已经很长一段时间了，但是我认为自己始终是一个门外汉，只是学习了一下这个基本的建模软件使用方法，以及一些相关的知识，虽然参加了一次这个电工杯的比赛，但是这个自身的实力和这个比赛的要求还是相差很远的，所以一直还在不断地进行这个学习提升自我，今天听了这个天津工业大学的汪晓银教授的讲课，真的感觉这个老师讲的超级棒，让我对于这个建模有了深刻的理解和体会；

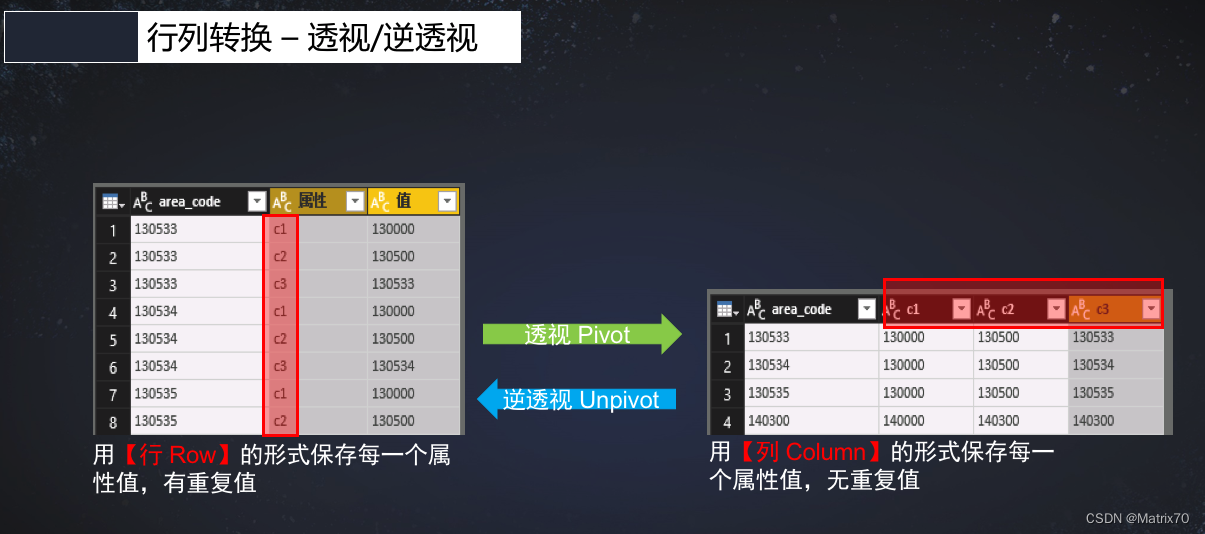
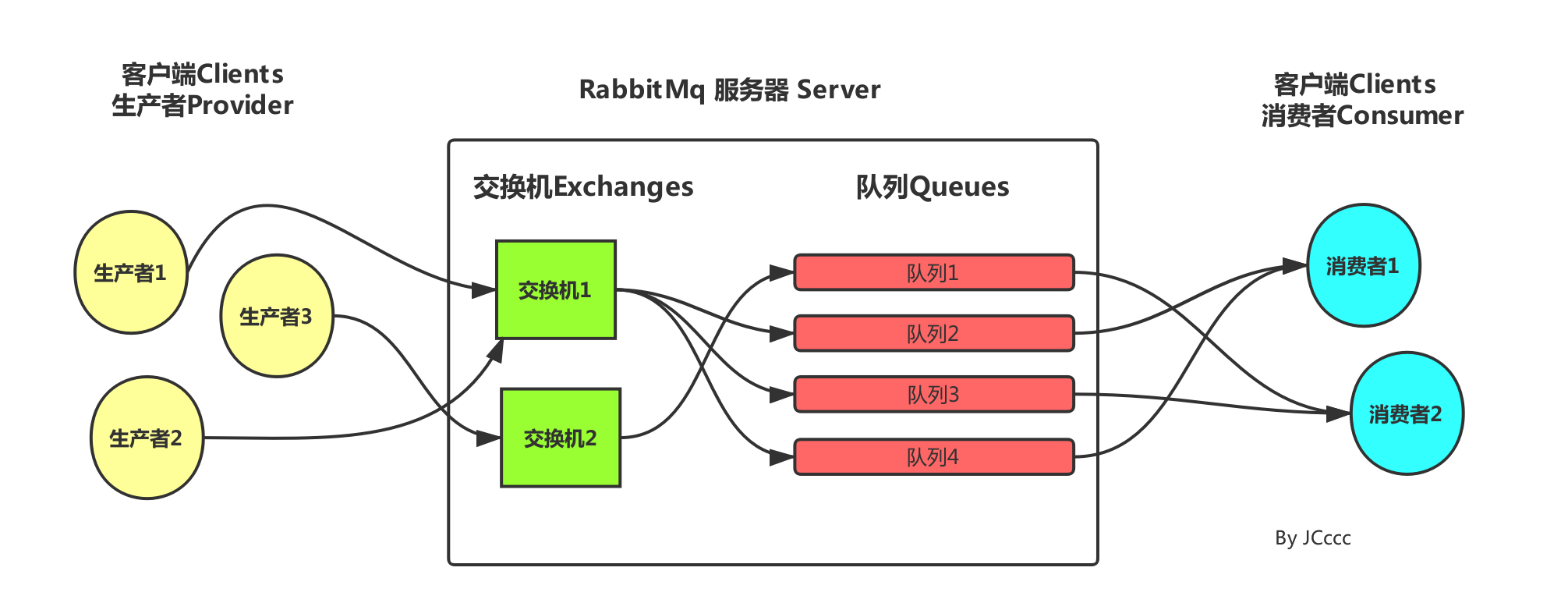
（2）对于下面的这个图片，对于每个初学数学建模的小白应该是再熟悉也不过了，但是我对于这个始终没有一个很清晰的理解，今天是通过这个包汤圆的问题深刻的体会了这个步骤；

（3）下面会先总结一下今天的这个数学建模的学习，再和大家简单的聊一聊这个包汤圆的问题； 

2.感受

（1）我是今天上午学习这个数学建模，发现一个很完整的视频，就是关于这个线性规划的，我只是无意之间点进去这个视频 ，因为是这个工大的，虽然这个学校也是位于这个天津市，但是自己对于这个学校没有什么了解，所以我就点进去了，但是听着听着就发现这个老师讲的真好，就去了解这个老师的更多的讲课视频，晚上才学习到这个包汤圆的问题；

（2）这个线性规划，就是属于运筹学里面的优化问题，这个前天天理的宋老师来我们学校进行这个数学建模的宣讲，这个老师的课件里面有一张就是这个数学建模涉及到的知识，第一项就是运筹学，当时感觉自己没有听说过，感觉还是挺高大上的，今天知道这个优化问题就是属于这个运筹学范畴才真正的对于这个运筹学有了更进一步的了解，后来还是特意的百度一下，发现这个运筹学涉及到的知识范围是非常宽的，他是属于这个管理学的知识（其实我对于这个不是很理解），包括这个决策等等之类的吧，这个优化问题就是决策问题，所以这个优化问题就和这个运筹学建立了联系吧，但是这个运筹学肯定是不会局限在这个优化问题上面的；

（3）这个优化问题我之前也是接触过，就是这个有一个目标函数和多个约束条件，这个求解最优的情况，分为这个单目标优化和多目标优化两类问题，这个多目标就是有多个目标函数，综合考虑多个目标函数得到这个最优解，比这个单目标规划求解起来肯定是更加复杂的；

（4）对于这个优化类的问题，今天还学习使用了一款软件，就是lingo软件，这个软件就是专门解决这个优化类问题而产生的，但是这个软件的功能肯定是不止于此的，其他方面的应用还等待着我去挖掘，但是目前肯定是要学习lingo在优化问题的使用,今天也是安装了一个并且已经上手使用了，感觉还是有一些难度的，但是这个操作页面很单一，学起来不会很困难，唯一不好的就是这个软件全英文；并不是很排斥英文，而是这个英文对于我们的这个软件的学习和使用稍微有一些困扰，但是对于我们的这个英语水平的提升肯定是潜移默化的；

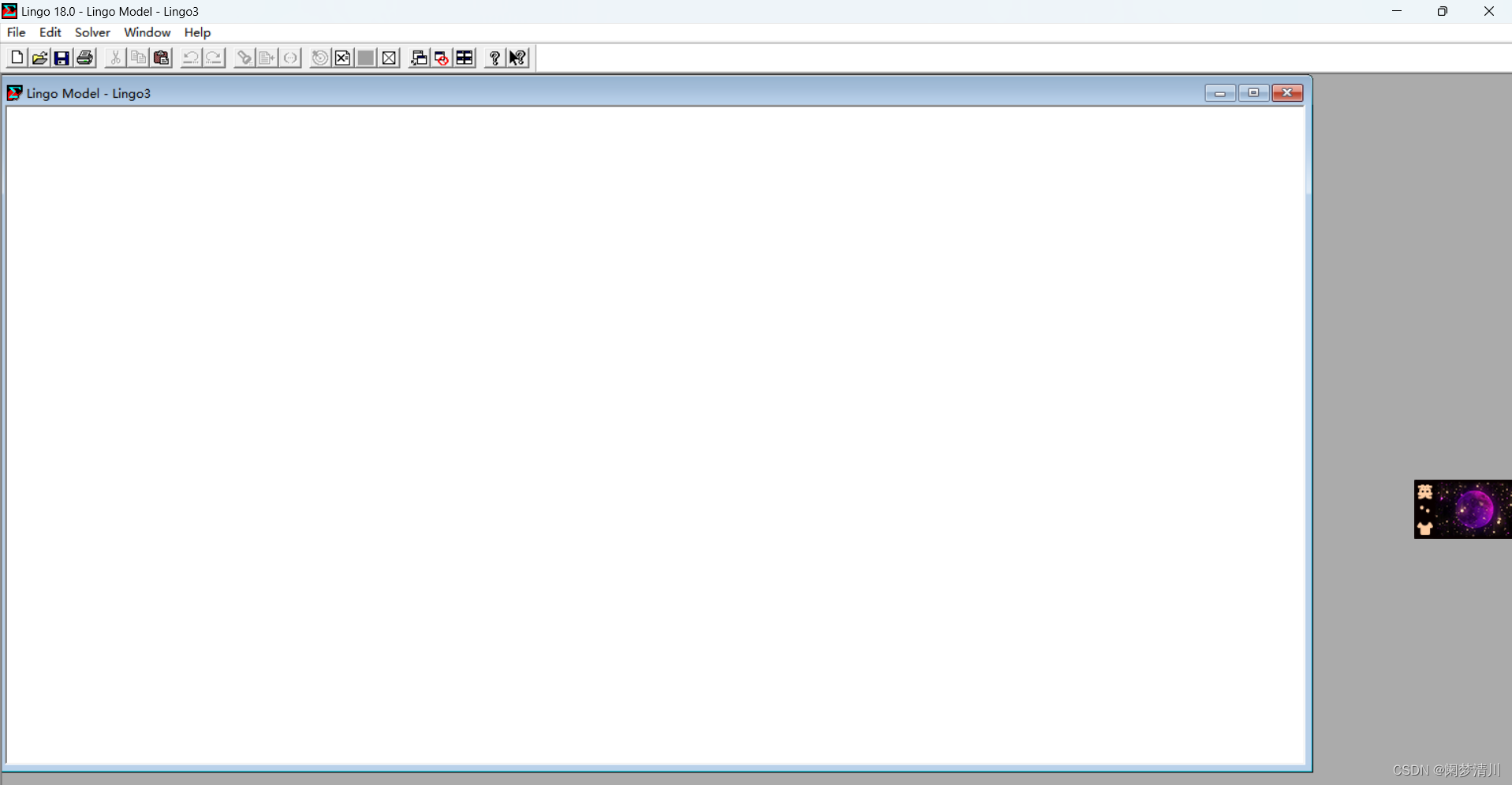
（5）这个软件我之前就是听说过的，但是这个真正的看到还是挺震惊的，上面的这个图片就是这个软件的操作页面，我们对于这个优化问题的求解基本上就是在这个软件上面去进行的（这个上面的工具栏里面的我现在还不是很理解），但是我知道的就是这个第一行向白纸一眼的就是创建一个新的窗口，这个页面是允许多个窗口同时存在的，但是一次只能运行一个窗口，然后点击上面的solve里面的这个solve就可以让这个程序运行了；

（6）我是选择这个一个汪教授上课的一个案例作为例子的，这个案例也是非常的经典优化问题，这个就是单目标的优化问题，之前是使用matlab的linprog函数处理的，但是具体哦是怎么处理的我已经不记得了，但是我觉得使用这个lingo软件去处理这个问题比这个MATLAB会更件容易，这个lingo上面的大部分代码我们是可以看懂的；

 

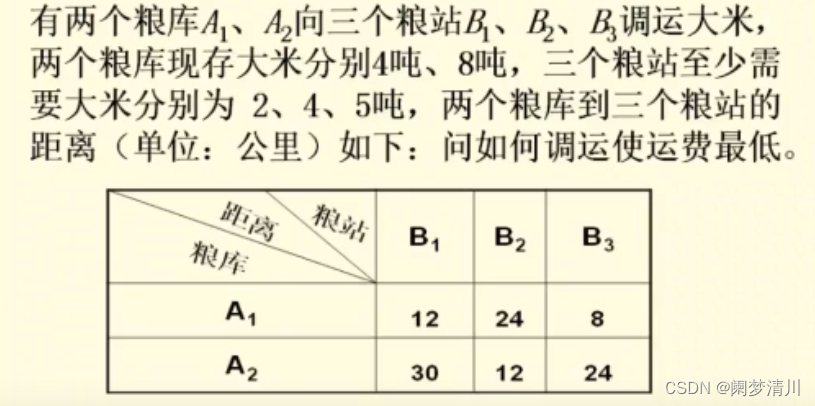
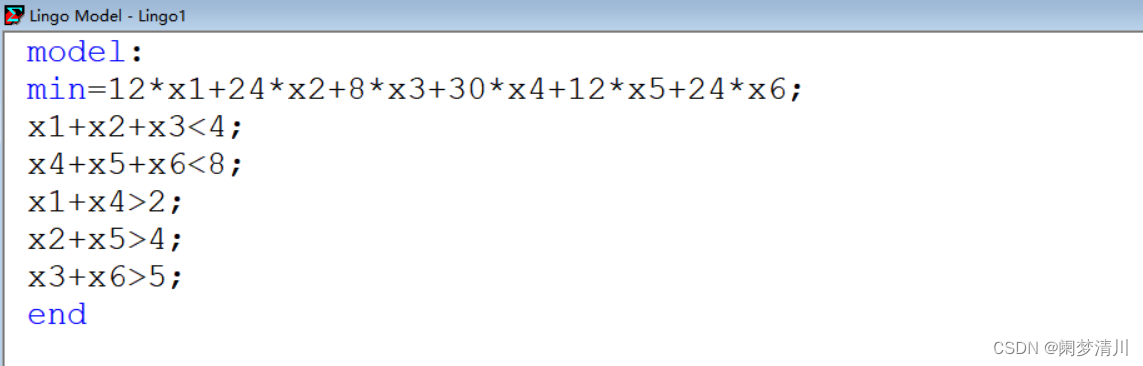
这个就是针对于上面的运粮食的问题，建立的模型，这个也非常容易理解，这个约束条件里面的就是这个运输的粮食不可以超过这个粮库的总量，而且这个每一个商店至少需要的粮食也是有这个最低要求的，我们这些作为这个约束条件，在这个数学里面使用这个s.t表示的就是约束条件，我们在这个高等数学的学习过程里面，也是遇到过这些问题的，我们学习的就是有条件的极值问题，用的就是这个拉格朗日乘数法进行这个求解的，但是那个是针对与只有一个或者少量的自变量而言的，我们要进行这个偏导数的求解，这个显然是不满足的，使用lingo，输入这个求解最小值的目标函数和这个五个约束条件就可以得到这个每个粮库向每一个商店运输的粮食的多少了；

（7）运行之后这个结果也是很显然的，最小的这个运费就是160，然后这个每一个粮库向每一个商店运输的粮食的数量上面也是有显示的；就是分别的这个对应的运输关系；

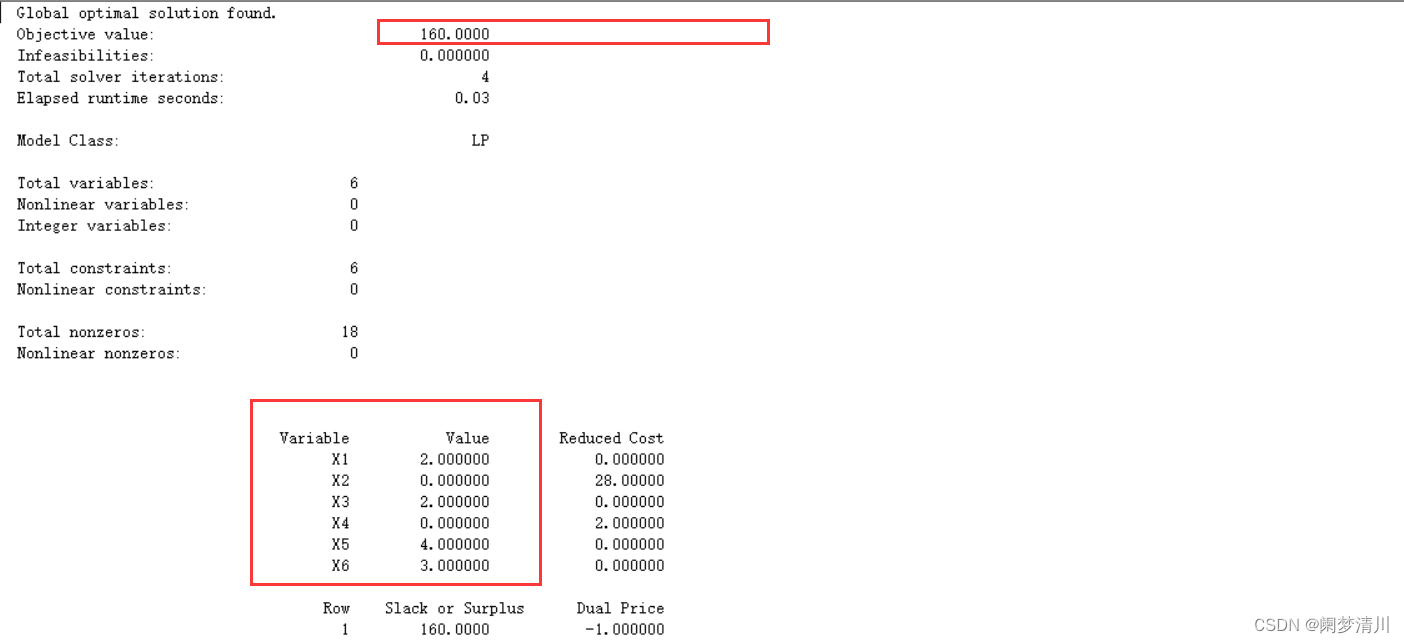
3.模型的反思

（1）实际上上面的这个lingo使用的方法叫做傻瓜编程 ，因为这个上面的语言都是我们熟悉的，而且我们是一共定义了6个变量，其实在汪教授组开始讲解这个方法的时候，我感觉这个lingo还是很容易的，就输入这个几行代码就求解出来了，而且好像这个lingo的语言和这个数学语言的契合度是比较高的，因为这个lingo里面的这个代码就是我们的数学表达式，只不过在lingo里面没有这个大于等于，小于等于号，只有大于号和小于号，仅此而已；

（2）如果你也是这样想的，那么你就大错特错了，因为上面的这个代码虽然简单，但是却不是我们想要的，我们需要的是数学语言，符号语言，上面的只是一种傻瓜式的写法，下面的才是我们真正应该掌握的；

（3）很显然，第二种写法使用这个表达式的方法，全是类似于这个数列的通项这样的式子，表达也是使用的求和符号，而不是普通的加号，这里好像还体会不到这个方法的精妙之处，因为这个题目的6个变量还不是很多，但是超过10个变量之后，我们使用这个方法的简洁性就体现了出来，因为这个只需要一个求和表达式，而上面的傻瓜编程需要一个一个的加起来，起码在这个代码长度上面就不一样了，我们的这个代码，强调的就是简洁，表达相同的问题，代码的简洁性可以体现这个编程者的能力，因此我们要学会上面的第二种解法，使用求和符号写出目标函数和约束条件；

（4）实际上这个老师说的很对，你对于这个数学问题，使用x1,x2,x3,x4,x5这些变量表达出来，还是使用求和运算表达出来，这个给老师的感觉是不一样的，如果你的这个变量的定义里面没有一个数字，全是通项这个形式，老师就会觉得你还是有东西的，这个就是汪教授说的，我感觉确实如此，从这个角度而言，我们也应该提高自己的这个能力；

（5）下面的这个就是在该情况下的代码，但是这个代码好像变长了，因为这个题目的变量比较少，因为这个里面涉及到这个段编程和求和函数，数组表示，我还没有学习，这里就不误人子弟了，感兴趣的同学可以自主进行学习；

 

4.包汤圆问题

（1）这个问题汪教授刚开始提出来的时候我还没有理解，看了三五遍才明白这个题目的意思，就是有这个一盆馅和一坨面团，这个面团把这个馅全部用完，可以包出来100个汤圆，现在这个面团不变，但是这个馅变多了，这个肯定就需要我们进行这个调整，现在的问题就是是多包几个还是少包几个；

（2）这个问题是什么意思了，就是这个馅变多了，我们原来是包了100个汤圆，我们现在可以包110个，这样就可能会把这个馅使用完，我们也可以包90个，这样每一个汤圆大一些，也可以把这个汤圆用完，现在问题就是多包几个还是少包几个汤圆，看似这个问题两个方式都可以，但是实际上这个问题的答案就是确定的，答案就是少包几个，为什么会这样呢，我们可以分析一下；

（3）按照上面的这个步骤，我们首先就是把这个问题转化为这个数学问题，怎么转化，这个也是数学建模需要的一种能力，因为这个建模的赛题里面也是一个实际问题，需要我们进行这个转化，这个题目的信息量比较少，因此转化起来并不是很困难，这个汤圆的话，无非就是这个面皮的面积，和这个汤圆的体积；

 （4）我们这个问题分析需要从体积进行这个分析，我们把这个看成一个超级大的汤圆，记作大V，变成无数个小汤圆之后，记作nv，我们需要进行比较的就是这个V和nv之间的大小关系，如果这个V>nv的话，我们需要少包几个，因为这个我们划分之后这个体积的和变小了，那么这个馅就放不下了，因此我们要少包几个，如果V<nv的话，我们就要多包几个（上面的这个过程可能不是很好理解，希望读者慢慢品味。我当时也是想了好久才明白的），推荐去看这个老师当时的讲解，视频的连接我放在下面了，值得去看一看；

数学建模https://www.bilibili.com/video/BV1R7411E7M4/?spm_id_from=333.788.recommend_more_video.14&vd_source=a432cb5e896a2b96961d1f73a6ebe0ca（5）模型假设，我们不可以不假设，也不可以假设过度，该考虑的我们还是要考虑的，什么叫做假设过度呢，就是我们不能过度的假设，这样的话这个模型也就没有必要建立了；

（6）通过这个数学的分析和运算之后，这个可以证明出来这个V>nv的，因此的话这个答案就是少包几个，我们可以进行这个模型的推广，例如生活里面的一瓶牙膏，这个商城进行活动，一大瓶药膏和多个小瓶牙膏，我们如何进行选择，这个问题本质上和这个包汤圆的问题是没有本质的区别的，这个就可以把我们建立的模型推广到有关的问题里面去，解决这一类问题，而不是一个问题；

（7）通过这个问题，我也是对于这个建模有了更进一步的理解，这个也是一个成长的过程吧，路漫漫其修远兮，吾将上下而求索~~~