第六十六天打卡 | 卡码网101 孤岛的总面积、卡码网102 沉没孤岛、卡码网103 水流问题、卡码网104 建造最大岛屿

卡码网101 孤岛的总面积

这一题在昨天的基础上，将比较得出最大孤岛面积的逻辑改为统计所有孤岛面积之和的逻辑即可。

最近做项目的时候也发现，很多时候代码逻辑能够复用最好就不要再自己写，防止出错，当然刷代码题的时候不一定是这个样子，就先偷个懒哈

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
 
int dir[4][2] = {-1, 0, 1, 0, 0, 1, 0, -1};
 
int bfs(vector<vector<int>>& grid, vector<vector<int>>& visited, int i_index, int j_index) {
    int sum = 0;
    queue<pair<int, int>> que;
    que.push(pair<int, int>(i_index, j_index));
    bool flag = true;
    while (!que.empty()) {
        // int num = que.size();
        // while (num--) {
            i_index = que.front().first;
            j_index = que.front().second;
            for (int i = 0; i < 4; i++) {
                if (i_index + dir[i][0] >= 0 && i_index + dir[i][0] < grid.size()) {
                    if (j_index + dir[i][1] >= 0 && j_index + dir[i][1] < grid[0].size()) {
                        if (grid[i_index+dir[i][0]][j_index+dir[i][1]] && 
                        !visited[i_index+dir[i][0]][j_index+dir[i][1]]) {
                            visited[i_index+dir[i][0]][j_index+dir[i][1]] = 1;
                            if (i_index+dir[i][0] == 0 || i_index+dir[i][0] == grid.size() - 1 
                            || j_index+dir[i][1] == 0 || j_index+dir[i][1] == grid[0].size() - 1)
                            {
                                
                                flag = false; 
                            }
                            sum++;
                            que.push(pair<int, int>(i_index+dir[i][0],j_index+dir[i][1]));
                        }
                    }
                }
            }   
            que.pop();
        // }
    }
    if (flag)
        return sum + 1;
    else return 0;
}
 
int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));
    vector<vector<int>> visited(n, vector<int>(m, 0));
    int sum = 0; 
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] && !visited[i][j]) {
                visited[i][j] = 1;
                // if (sum < bfs(grid, visited, i, j))
                if (i == 0 || i == grid.size() - 1 || j == 0 || j == grid[0].size() - 1)
                {
                    bfs(grid, visited, i, j);   
                }
                else 
                    sum += bfs(grid, visited, i, j);
                    // cout << sum << endl;
            }
        }
    }
    cout << sum << endl;
    return 0;
}

卡码网102 沉没孤岛

先要用一个bfs的逻辑或者一个dfs的逻辑判断是否是孤岛，即是否遍历到的横向或者纵向相连的所有节点都不和最外层边界直接触碰，这里传参数有个技巧，原本都是用的引用，这里在传入visited数组的时候不用加引用符对原visited数组进行修改，否则就是直接在遍历了。

在第二次修改孤岛的时候再用原先的visited数组加上引用就行。

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
 
int dir[4][2] = {-1, 0, 1, 0, 0, 1, 0, -1};
 
 /*
  * Description: 判断是否是孤岛
  */
 
bool ifIsolated(vector<vector<int>>& grid, vector<vector<int>> visited, int i_index, int j_index) {
    queue<pair<int, int>> que;
    que.push(pair<int, int>(i_index, j_index));
    bool flag = true;
    while (!que.empty()) {
        // int num = que.size();
        // while (num--) {
            i_index = que.front().first;
            j_index = que.front().second;
            for (int i = 0; i < 4; i++) {
                if (i_index + dir[i][0] >= 0 && i_index + dir[i][0] < grid.size()) {
                    if (j_index + dir[i][1] >= 0 && j_index + dir[i][1] < grid[0].size()) {
                        if (grid[i_index+dir[i][0]][j_index+dir[i][1]] && 
                        !visited[i_index+dir[i][0]][j_index+dir[i][1]]) {
                            visited[i_index+dir[i][0]][j_index+dir[i][1]] = 1;
                            if (i_index+dir[i][0] == 0 || i_index+dir[i][0] == grid.size() - 1 
                            || j_index+dir[i][1] == 0 || j_index+dir[i][1] == grid[0].size() - 1)
                            {
                                
                                flag = false; 
                            }
                            que.push(pair<int, int>(i_index+dir[i][0],j_index+dir[i][1]));
                        }
                    }
                }
            }   
            que.pop();
        // }
    }
    return flag;
} 

/*
 * 
 * Description: 孤岛取反
 */
void bfs(vector<vector<int>>& grid, vector<vector<int>>& visited, int i_index, int j_index, bool flag) {
    if (flag) grid[i_index][j_index] = 0;
    queue<pair<int, int>> que;
    que.push(pair<int, int>(i_index, j_index));
    while (!que.empty()) {
            i_index = que.front().first;
            j_index = que.front().second;
            for (int i = 0; i < 4; i++) {
                if (i_index + dir[i][0] >= 0 && i_index + dir[i][0] < grid.size()) {
                    if (j_index + dir[i][1] >= 0 && j_index + dir[i][1] < grid[0].size()) {
                        if (grid[i_index+dir[i][0]][j_index+dir[i][1]] && 
                        !visited[i_index+dir[i][0]][j_index+dir[i][1]]) {
                            visited[i_index+dir[i][0]][j_index+dir[i][1]] = 1;
                            if (flag == true) 
                                grid[i_index+dir[i][0]][j_index+dir[i][1]] = 0;
                            que.push(pair<int, int>(i_index+dir[i][0],j_index+dir[i][1]));
                        }
                    }
                }
            }   
            que.pop();
        // }
    }
}
 
int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));
    vector<vector<int>> visited(n, vector<int>(m, 0));
    bool flag = true;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] && !visited[i][j]) {
                visited[i][j] = 1;
                // if (sum < bfs(grid, visited, i, j))
                if (i == 0 || i == grid.size() - 1 || j == 0 || j == grid[0].size() - 1)
                {
                    flag = false;
                    bfs(grid, visited, i, j, flag);   
                }
                else {
                    flag = ifIsolated(grid, visited, i, j);
                    bfs(grid, visited, i, j, flag);   
                }
            }
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cout << grid[i][j] << ' ';
        }
        cout << endl;
    }
    return 0;
}

卡码网103 水流问题

训练营越到后面，其实是越来越顺的，一方面是有了动量和习惯气的支撑，另一方面也是前面的知识和编程技巧掌握了之后对于后面的解题很自然而然就用到了，所以建议前面的题目还是要认真刷，有时间的话建议也像这样子每天写个博客总结记录下，后面可以当成笔记来复习的。

这一题逻辑和前面的就比较像，可以自行进行思考尝试，这里给出我写的代码，权当抛砖引玉了

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
 
int dir[4][2] = {-1, 0, 1, 0, 0, 1, 0, -1};
 
 /*
  * Description: 判断是否是符合条件的点
  */
 
bool ifAble(vector<vector<int>>& grid, vector<vector<int>> visited, int i_index, int j_index) {
    queue<pair<int, int>> que;
    que.push(pair<int, int>(i_index, j_index));
    bool flagl_u = false;
    bool flagr_d = false;
    if (i_index == 0 ||  j_index == 0)
    {
        flagl_u = true; 
    }
    if (i_index == grid.size() - 1 || j_index == grid[0].size() - 1) {
        flagr_d = true;
    }
    if (flagl_u && flagr_d) return true;
    while (!que.empty()) {
            i_index = que.front().first;
            j_index = que.front().second;
            for (int i = 0; i < 4; i++) {
                if (i_index + dir[i][0] >= 0 && i_index + dir[i][0] < grid.size()) {
                    if (j_index + dir[i][1] >= 0 && j_index + dir[i][1] < grid[0].size()) {
                        if (grid[i_index+dir[i][0]][j_index+dir[i][1]] <= grid[i_index][j_index] &&
                        !visited[i_index+dir[i][0]][j_index+dir[i][1]]) {
                            visited[i_index+dir[i][0]][j_index+dir[i][1]] = 1;
                            if (i_index+dir[i][0] == 0 ||  j_index+dir[i][1] == 0)
                            {
                                flagl_u = true; 
                            }
                            if (i_index+dir[i][0] == grid.size() - 1 || j_index+dir[i][1] == grid[0].size() - 1) {
                                flagr_d = true;
                            }
                            if (flagl_u && flagr_d) return true;
                            que.push(pair<int, int>(i_index+dir[i][0],j_index+dir[i][1]));
                        }
                    }
                }
            }   
            que.pop();
        // }
    }
    return flagl_u && flagr_d;
} 

 
int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));
    vector<vector<int>> visited(n, vector<int>(m, 0));
    bool flag = true;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (ifAble(grid, visited, i, j)) {
                cout << i << ' ' << j << endl;
            }
        }
    }
    return 0;
}

卡码网104 建造最大岛屿

（暂时没想出来，给出题解如下，可自行学习，后面再改改）

每次深搜遍历计算最大岛屿面积，都做了很多重复的工作。

只要用一次深搜把每个岛屿的面积记录下来就好。

第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积

第二步：再遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出选一个0变成1 之后的最大面积。

拿如下地图的岛屿情况来举例：（1为陆地）

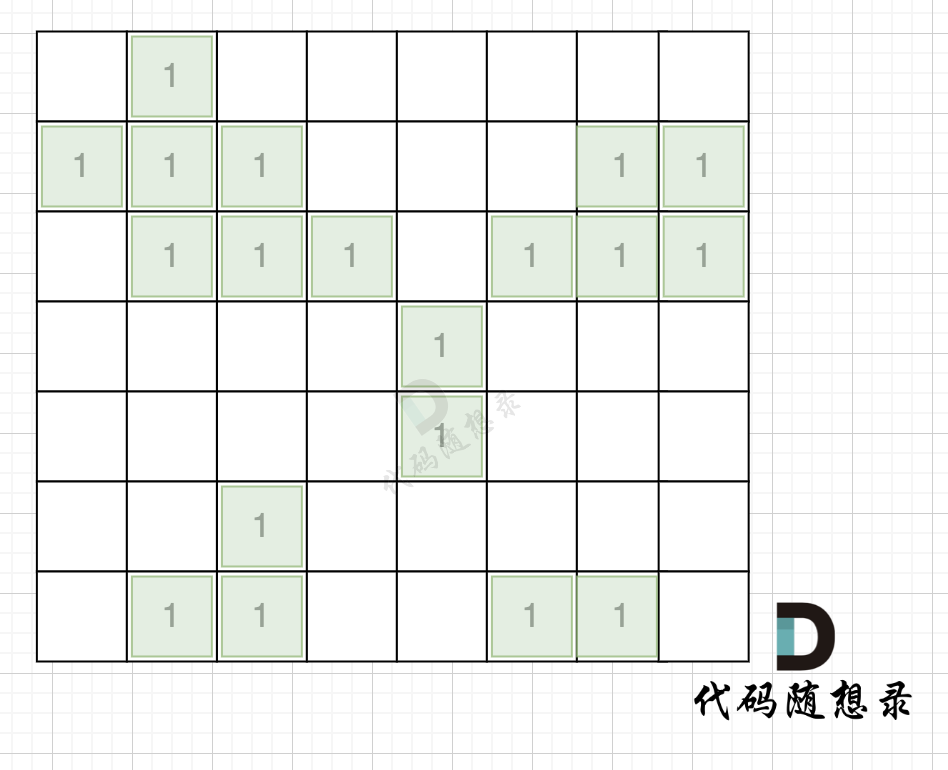
第一步，则遍历题目，并将岛屿到编号和面积上的统计，过程如图所示：

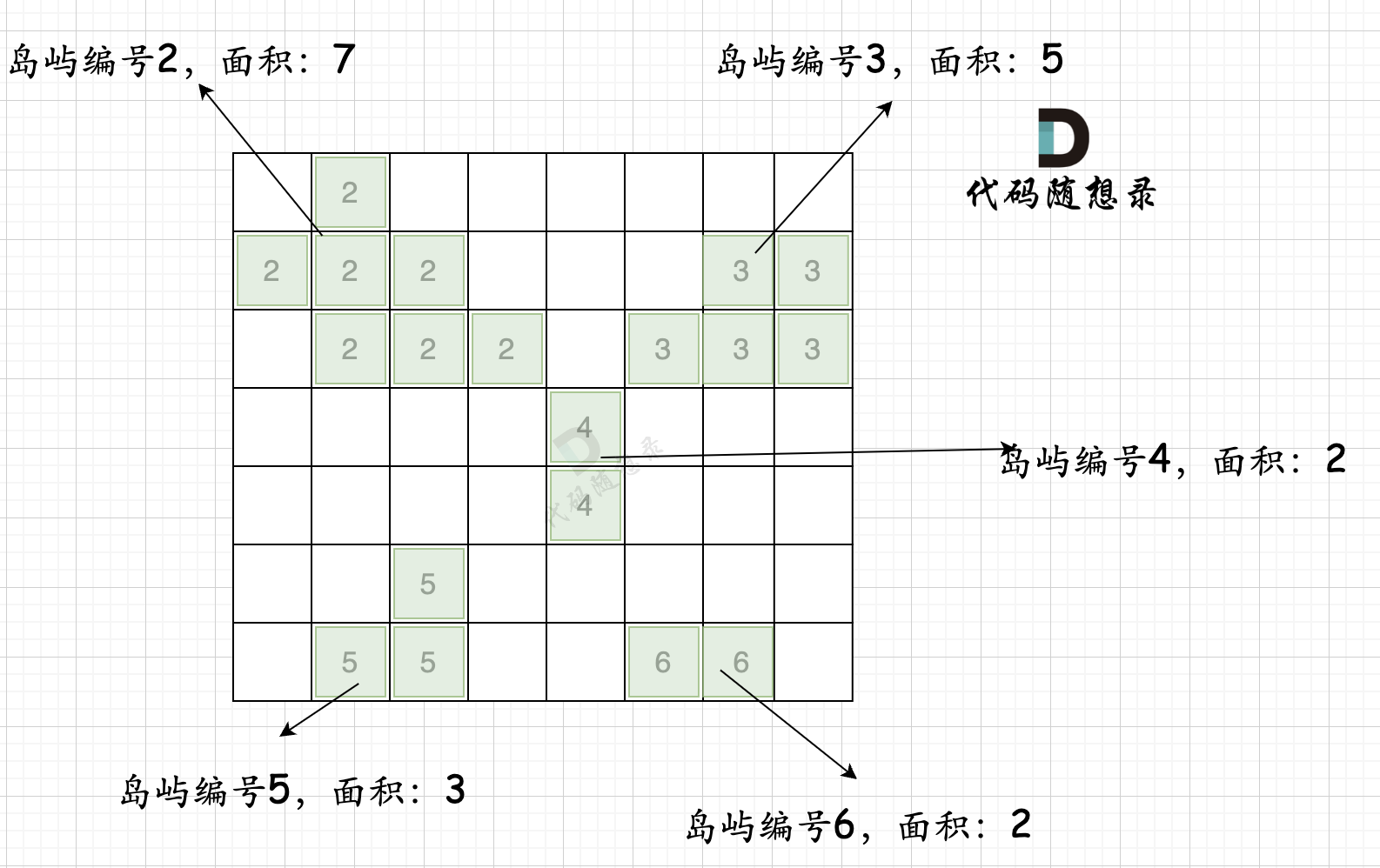
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
    if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
    visited[x][y] = true; // 标记访问过
    grid[x][y] = mark; // 给陆地标记新标签
    count++;
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
        dfs(grid, visited, nextx, nexty, mark);
    }
}

int largestIsland(vector<vector<int>>& grid) {
    int n = grid.size(), m = grid[0].size();
    vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false)); // 标记访问过的点
    unordered_map<int ,int> gridNum;
    int mark = 2; // 记录每个岛屿的编号
    bool isAllGrid = true; // 标记是否整个地图都是陆地
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 0) isAllGrid = false;
            if (!visited[i][j] && grid[i][j] == 1) {
                count = 0;
                dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
                gridNum[mark] = count; // 记录每一个岛屿的面积
                mark++; // 记录下一个岛屿编号
            }
        }
    }
}