Location: Beijing
1 大模型剪枝

剪枝的理论来源基于彩票假设(Lottery Ticket Hypothesis),指在神经网络中存在一种稀疏连接模式,即仅利用网络的一小部分连接(彩票)就足以实现与整个网络相当的性能。
2 神经网络结构搜索(NAS)
首先介绍这个论文的一些基础
2.1 引言
神经网络(Fig. 2.1)的超参数有两类,分别是Architecture和Algorithm,对于Architecture比如神经网络的层数、每层神经元个数、激活函数、卷积核的大小等;对于Algorithm如用的算法种类,算法学习率、batch_size、Epochs数量等。这些超参数怎么自动调是个问题。
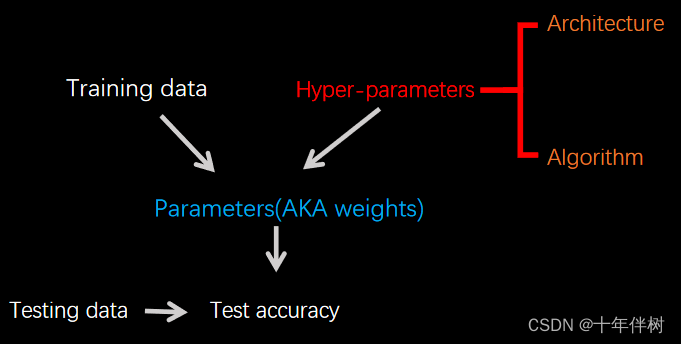
以CNN为例,Architecture超参数有:
1.卷积层的数量和全连接层的数量;
2.每个卷积层中卷积核数量大小和步长;
3.全连接层的宽度。
如果手动调节这些超参数,工作量是巨大的,而且有点捞。自动调节算法呼之欲出:神经网络结构搜索(NAS)
2.2 NAS(神经网络结构搜索)
NAS1的基本思想是使用搜索算法在给定的搜索空间中探索各种可能的网络结构,并根据预定义的目标或约束进行评估和比较。搜索空间可以包括不同的网络层类型(卷积层、循环层等)、层数、宽度、连接模式等。搜索算法可以采用随机搜索、进化算法、强化学习等方法。
比如,我们想做一个20层的卷积神经网络,其中卷积核的搜索空间如Fig. 2.2
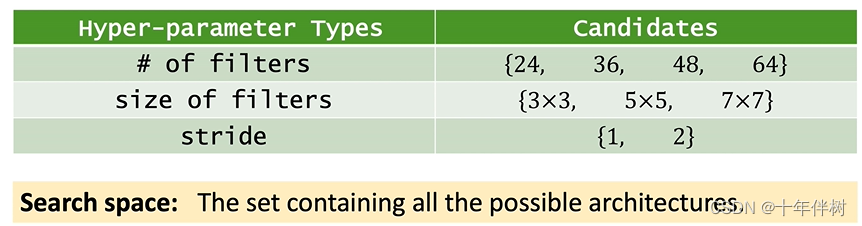
理想状态下算法会给20层卷积遍历所有搜索空间,有 ( 4 × 3 × 2 ) 20 (4×3×2)^{20} (4×3×2)20种不同的选择。
2.3 随机搜索
通过交叉验证的方法找出较优解
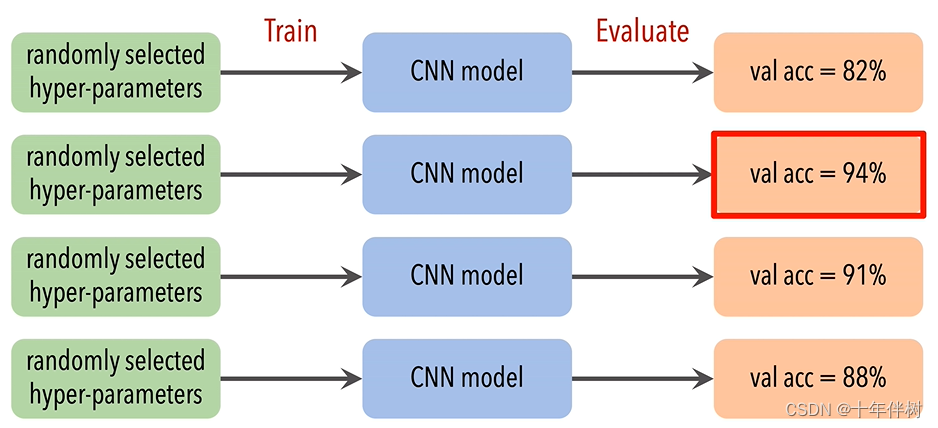
可以看出NAS的难点,每次抽取一组超参数都需要经历“搭建模型-模型初始化-训练-评估”的过程,每一组代价都很大,更何况是从
(
4
×
3
×
2
)
20
(4×3×2)^{20}
(4×3×2)20种方案中找到最优解。
这里需要指出一点,比如给定一个不复杂的分类任务,那神经网络的结构就不会复杂,说明结构最优解并不是完全随机分布在搜索空间的。我们使用val acc来评价生成的CNN网络的好坏,然而可以看到,搜索空间中的变量并不是val acc的可微变量,故而不能用反向传播的方法来找到最优解,这种不可微的问题往往可以使用强化学习的方法来寻找最优解。然而根据论文2的基于RNN寻找最优网络架构,不光要训练不同结构的CNN还要训练一个RNN,简直是脱裤子放屁。
2.4 可微NAS
仍然以上面搭建一个20层的CNN的神经网络,我们对每一层提供9个备选方案,然后再然后再剔除八个较差方案,那就从一定概率上找的了较优解,这种思想叫Super-net。
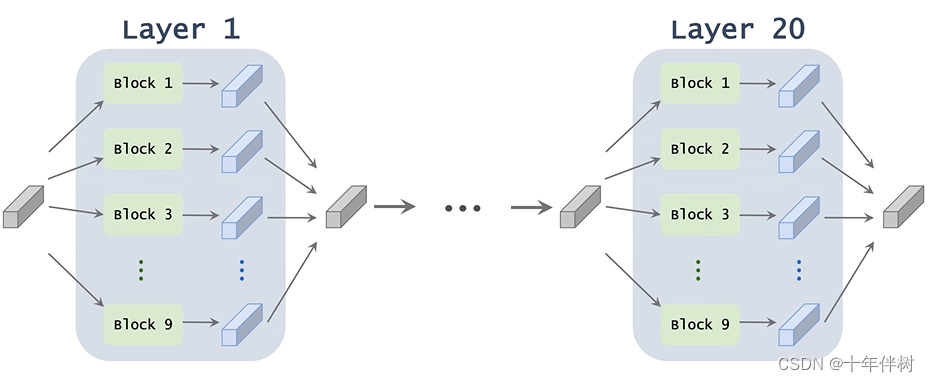
挺像图搜索算法的。其中Super-net的每个layer如下图
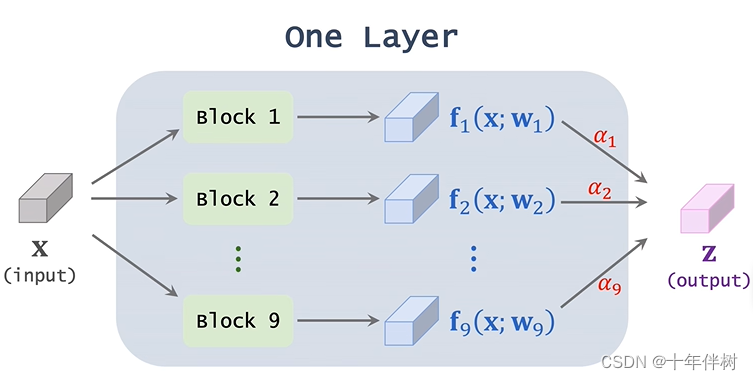
其中
X
X
X指这一层的输入,
B
l
o
c
k
i
Block \mathcal{i}
Blocki指的是候选模块,
w
w
w指的是候选模块的权重,
f
i
\mathcal{f}_i
fi指输入经过候选模块后的结果,对所有
f
\mathcal{f}
f做加权平均得到
z
z
z,权重用
α
i
\alpha_{i}
αi表示(
α
i
\alpha_{i}
αi用softmax求得,目的是让其和为1。其中Super-net的学习目标就是学习这些
α
i
\alpha_{i}
αi,最终确定保留哪个备选块。
这样Super-net就变成了可微函数,可以用来反向传播。
这里需要指出的是,当考虑到模型部署到资源受限的设备时,并非模型的性能越小越好,还需要限制模型的复杂程度,这样可以考虑在损失函数中添加资源约束,以满足要求。如此一来,损失函数就由两部分组成:任务损失和资源约束损失,这与正则化的思想极其相似。
2.5 小节
最后依据NAS方法将其搜索策略分为两类:随机搜索方法和基于梯度的方法
3 DMS
基于2.4小节,虽然Super-net是可微模型,但也只是对
α
i
\alpha_{i}
αi可微,按道理来说,对于一个“解决模型结构超参数”的模型,应该直接对超参数可微才对。(加粗的“直接”与下文的“直接和可微”中的“直接”对应)
DMS3(Differentiable Model Scaling using Differentiable Topk,基于可微Topk的可微模型缩放)期望能够找到直接和可微的模式来梯度下降,
引入了一个完全可微的topk算子,以直接可微的方式建模模型的深度(网络的深度指的是网络中层数的数量,即网络中堆叠的层的数量)和宽度(网络的宽度指的是网络中每一层的神经元数量),每个可微topk算子都有一个可学习参数,表示深度或宽度结构超参数,可以基于任务损失和资源约束损失(2.4有提到)进行优化。
3.1 可微topk
假设有一个结构超参数
k
k
k(k<N),
k
k
k表示元素的数量;使用
c
∈
R
N
c\in\mathbb{R}^{N}
c∈RN来代表元素的重要度,
c
c
c越大,元素越重要;可微topk的目标是输出一个掩膜器(mask)
m
∈
[
0
,
1
]
N
m\in[0,1]^{N}
m∈[0,1]N,代表top k的重要元素。
以往的topk算子是设立一个阈值
a
a
a,当元素的重要度
c
[
i
]
c[i]
c[i]大于
a
a
a,保留该元素,
a
a
a是个可学习参数,
k
=
∑
i
=
1
N
1
[
c
i
>
a
]
k=\sum_{i=1}^N1[c_i>a]
k=∑i=1N1[ci>a]。这个公式1每一块都需要用到,可表示为
m
i
=
f
(
a
)
≈
{
1
if
c
i
>
a
0
otherwise
(1)
m_i=f(a)\approx\begin{cases}1&\text{if} c_i>a\\0&\text{otherwise}\end{cases}\tag{1}
mi=f(a)≈{10ifci>aotherwise(1)
从公式1可以看出
f
f
f是个分段函数,不可微,往往采用梯度估计的方法来实现反向传播。对
a
a
a使用完全可微的
f
f
f的难点是通道重要度
c
[
i
]
c[i]
c[i]的分布不均匀。比如
c
[
i
]
c[i]
c[i]不均匀的分布在[0,100],假设
a
a
a在每次迭代中加1,当
c
[
i
]
c[i]
c[i]和
c
[
i
+
1
]
c[i+1]
c[i+1]跨度很大,
a
a
a需要很多次迭代来跨越
c
[
i
]
c[i]
c[i]和
c
[
i
+
1
]
c[i+1]
c[i+1]。当
c
[
i
]
c[i]
c[i]和
c
[
i
+
1
]
c[i+1]
c[i+1]差异很小,
a
a
a可能一步中跨越多个元素。因此,当元素的重要度
c
[
i
]
c[i]
c[i]不均匀时,以完全可区分的方式优化
a
a
a很难。
为了解决这个问题,采用了一个重要度
c
[
i
]
c[i]
c[i]标准化过程,强制将不均匀分布的重要度
c
[
i
]
c[i]
c[i]转换为均匀分布的值,使topk函数光滑,易于以可微的方式优化。综上,可微topk有两个步骤:重要度
c
[
i
]
c[i]
c[i]归一化和软掩模生成。
3.1.1 重要度 c [ i ] c[i] c[i]及其归一化
重要度的评价方法有指数度量、SNIP、Fisher和泰勒4重要度分析(第四章介绍),本文使用泰勒重要度分析+移动基准线,可用以下公式2表示,原因是移动基准线可以提高泰勒重要度的性能,至于为什么不用SNIP和Fisher,文章指出用泰勒重要度分析性能已经足够。
c
i
t
+
1
=
c
i
t
×
d
e
c
a
y
+
(
m
i
t
×
g
i
)
2
×
(
1
−
d
e
c
a
y
)
(2)
c_i^{t+1}=c_i^t\times decay+(m_i^t\times g_i)^2\times(1-decay)\tag{2}
cit+1=cit×decay+(mit×gi)2×(1−decay)(2)
式中,
t
t
t表示训练步骤,
g
i
g_i
gi是
m
i
m_i
mi对训练损失的梯度,
d
e
c
a
y
decay
decay是指衰减率,初始值
c
i
0
c_i^0
ci0设为零,衰减率设为0.99。
将所有元素的重要度映射到从0到1的均匀分布的值,根据经验,往往
c
i
c_i
ci≠
c
j
c_j
cj
c
i
′
=
1
N
∑
j
=
1
N
1
[
c
i
>
c
j
]
(3)
c'_i=\frac{1}{N}\sum_{j=1}^N1[c_i>c_j]\tag{3}
ci′=N1j=1∑N1[ci>cj](3)
如此一来,
a
a
a也就有了一个新定义:剪枝比。
3.1.2 软掩模生成
归一化后,基于剪枝比
a
a
a的相对大小和归一化元素重要性
c
′
c'
c′,使用光滑可微函数公式4生成软掩模
m
m
m
m
i
=
f
(
a
)
=
S
i
g
m
o
i
d
(
λ
(
c
i
′
−
a
)
)
=
1
1
+
e
−
λ
(
c
i
′
−
a
)
(4)
m_i=f(a)=\mathrm{Sigmoid}(\lambda(c_i'-a))=\frac{1}{1+e^{-\lambda(c_i'-a)}}\tag{4}
mi=f(a)=Sigmoid(λ(ci′−a))=1+e−λ(ci′−a)1(4)
式中,
λ
\lambda
λ是一个超参数,用来控制从公式3到一个硬掩模函数的逼近程度,通常
λ
=
N
\lambda=N
λ=N,这意味着除了中间几个重要度,其他都接近0或1,误差小于0.05。
4 泰勒重要度分析
给定一个神经网络权重参数
W
=
{
w
0
,
w
1
,
.
.
.
,
w
M
}
\mathbf{W}=\{w_0,w_1,...,w_M\}
W={w0,w1,...,wM},一个数据集
D
=
{
(
x
0
,
y
0
)
,
(
x
1
,
y
1
)
,
.
.
.
,
(
x
K
,
y
K
)
}
\mathcal{D} = \{(x_{0},y_{0}),(x_{1},y_{1}),...,(x_{K},y_{K})\}
D={(x0,y0),(x1,y1),...,(xK,yK)},其中
x
i
x_i
xi是输入,
y
i
y_i
yi是输出,训练的目的是使误差
E
E
E最小,
E
E
E的表达式如公式5
min
W
E
(
D
,
W
)
=
min
W
E
(
y
∣
x
,
W
)
(5)
\min_\mathbf{W}E(\mathcal{D},\mathbf{W})=\min_\mathbf{W}E(y|x,\mathbf{W})\tag{5}
WminE(D,W)=WminE(y∣x,W)(5)
在剪枝的情况下,为了保证矩阵的稀疏性,这里添加一个稀疏化项,如公式6
min
W
E
(
D
,
W
)
+
λ
∣
∣
W
∣
∣
0
(6)
\min_\mathbf{W}E(\mathcal{D},\mathbf{W})+\lambda||\mathbf{W}||_0\tag{6}
WminE(D,W)+λ∣∣W∣∣0(6)
式中,
λ
\lambda
λ是一个缩放系数,
∣
∣
⋅
∣
∣
0
||·||_0
∣∣⋅∣∣0指非零元素的
ℓ
0
\ell_{0}
ℓ0范数,事实上,并没有具体的方法来实现最小化
ℓ
0
\ell_{0}
ℓ0范数,因为它是非凸的, 且NP-hard。
一种方法是在原始优化公式(5)收敛后,从完整的参数
W
W
W开始,逐渐将该参数
W
W
W每次减少几个参数。在这个增量设置中,可以通过单独考虑每个参数的重要性,假设参数的独立性来决定删除哪些参数。我们将这种对全组合搜索的简化近似称为贪婪一阶搜索。
一个参数的重要度可以通过去除它所引起的误差来量化。在一个i.i.d.下假设,该误差可以为有和没有参数(
w
m
w_m
wm)的预测误差的平方差:
I
m
=
(
E
(
D
,
W
)
−
E
(
D
,
W
∣
w
m
=
0
)
)
2
(7)
\mathcal{I}_m=\left(E(\mathcal{D},\mathbf{W})-E(\mathcal{D},\mathbf{W}|w_m=0)\right)^2\tag{7}
Im=(E(D,W)−E(D,W∣wm=0))2(7)
计算神经网络中每个参数的
I
m
\mathcal{I}_m
Im代价很大,可以通过二阶泰勒展开来近似
W
W
W附近的
I
m
\mathcal{I}_m
Im
I
m
(
2
)
(
W
)
=
(
g
m
w
m
−
1
2
w
m
H
m
W
)
2
(8)
\mathcal{I}_m^{(2)}(\mathbf{W})=\left(g_mw_m-\frac12w_m\mathbf{H}_m\mathbf{W}\right)^2\tag{8}
Im(2)(W)=(gmwm−21wmHmW)2(8)
式中
g
m
=
∂
E
∂
w
m
g_m=\frac{\partial E}{\partial w_m}
gm=∂wm∂E是梯度
g
g
g中的元素,
H
i
,
j
=
∂
2
E
∂
w
i
∂
w
j
H_{i,j}=\frac{\partial^2E}{\partial w_i\partial w_j}
Hi,j=∂wi∂wj∂2E是Hessian5
H
H
H(第五章展开讲Hessian矩阵)中的元素,
H
m
H_m
Hm指
H
H
H中的第
m
m
m行,式中的平方不是泰勒展开的平方,平方项是保证误差结果非负,实际上是对
E
(
D
,
W
)
E(\mathcal{D},\mathbf{W})
E(D,W)和
E
(
D
,
W
∣
w
m
=
0
)
E(\mathcal{D},\mathbf{W}|w_m=0)
E(D,W∣wm=0)分别展开做差再取平方,甚至可以利用一阶展开式计算了一个更紧凑的近似,并简化为
I
m
(
1
)
(
W
)
=
(
g
m
w
m
)
2
(9)
\mathcal I_m^{(1)}(\mathbf{W})=\left(g_mw_m\right)^2\tag{9}
Im(1)(W)=(gmwm)2(9)
一阶泰勒近似的是非常好处理的,因为梯度
g
g
g就在反向传播中。本文后面的内容都来自一阶泰勒展开,下面公式10可以看到一阶重要度近似的集合
I
(
1
)
(
W
)
=
{
I
1
(
1
)
(
W
)
,
I
2
(
1
)
(
W
)
,
.
.
.
,
I
M
(
1
)
(
W
)
}
(10)
\mathbf{I}^{(1)}(\mathbf{W}) = \{\mathcal{I}_1^{(1)}(\mathbf{W}),\mathcal{I}_2^{(1)}(\mathbf{W}),...,\mathcal{I}_M^{(1)}(\mathbf{W})\}\tag{10}
I(1)(W)={I1(1)(W),I2(1)(W),...,IM(1)(W)}(10)
为了表示一组权重
W
S
\mathbf{W}_\mathcal{S}
WS(比如一个卷积核)的重要度(这里我们命名叫联合重要度),可以将其定义为联合重要度公式11,或者直接对这个剪枝群的重要度求和为联合重要度如公式12
I
S
(
1
)
(
W
)
≜
(
∑
s
∈
S
g
s
w
s
)
2
(11)
\mathcal{I}_{\mathcal{S}}^{(1)}(\mathbf{W})\triangleq\left(\sum_{s\in S}g_sw_s\right)^2\tag{11}
IS(1)(W)≜(s∈S∑gsws)2(11)
I
^
S
(
1
)
(
W
)
≜
∑
s
∈
S
I
s
(
1
)
(
W
)
=
∑
s
∈
S
(
g
s
w
s
)
2
(12)
\widehat{\mathcal{I}}_{\mathcal{S}}^{(1)}(\mathbf{W})\triangleq\sum_{s\in\mathcal{S}}\mathcal{I}_{s}^{(1)}(\mathbf{W})=\sum_{s\in\mathcal{S}}(g_{s}w_{s})^{2}\tag{12}
I
S(1)(W)≜s∈S∑Is(1)(W)=s∈S∑(gsws)2(12)
这两个公式只是对联合重要度一种个人定义,并无具体深层次的数学含义,式中,
S
\mathcal{S}
S表示剪枝
w
w
w的集合,这里的
s
\mathcal{s}
s与前面公式里的下标的
m
\mathcal{m}
m指向相同。可以从公式11和12看出,联合重要度只是先单独去掉一个一个的权重,再以某种方式求和。
为了深入了解这两种方法,并简化计算,论文在网络中添加了“门控机制”,
z
=
1
M
z = 1^M
z=1M,权重为1,维数等于神经元的数量
M
M
M(
W
\mathbf{W}
W的元素个数)。门控层使重要度计算更容易,因为它们不参与优化;而且有一个常数值,因此允许
W
W
W不用经过公式8-12计算。如果一个门控
z
m
z_m
zm遵循一个由权值
W
s
∈
S
m
W_{s∈S_m}
Ws∈Sm参数化的神经元,那么重要性近似
I
m
(
1
)
\mathcal{I}_m^{(1)}
Im(1)为:
I
m
(
1
)
(
z
)
=
(
∂
E
∂
z
m
)
2
=
(
∑
s
∈
S
m
g
s
w
s
)
2
=
I
S
m
(
1
)
(
W
)
(13)
\mathcal{I}_m^{(1)}(\mathbf{z})=\left(\frac{\partial E}{\partial\mathbf{z}_m}\right)^2=\left(\sum_{s\in\mathcal{S}_m}g_sw_s\right)^2=\mathcal{I}_{\mathcal{S}_m}^{(1)}(\mathbf{W})\tag{13}
Im(1)(z)=(∂zm∂E)2=(s∈Sm∑gsws)2=ISm(1)(W)(13)
式中,
S
S
S表示计算前一层输出所需的内部维度,例如线性层的输入维度,或卷积层的空间维度和输入维度。可以看到,门的重要性等价于参数群体对前一层参数的贡献。
通过一些操作,可以将上述所提出的方法与信息论联系起来。让
h
m
=
∂
E
∂
z
m
=
g
s
∈
S
m
T
W
s
∈
S
m
\mathbf{h}_{m}=\frac{\partial E}{\partial\mathbf{z}_{m}}=\mathbf{g}_{s\in\mathcal{S}_{m}}^{T}\mathbf{W}_{s\in\mathcal{S}_{m}}
hm=∂zm∂E=gs∈SmTWs∈Sm,并观察
h
m
\mathbf{h}_{m}
hm的方差(假设在收敛时有
E
(
h
m
)
2
=
0
\mathbb{E}(\mathbf{h}_m)^2=0
E(hm)2=0):
V
a
r
(
h
m
)
=
E
(
h
m
2
)
−
E
(
h
m
)
2
=
I
(
1
)
(
z
)
(14)
\mathrm{Var}(\mathbf{h}_m)=\mathbb{E}(\mathbf{h}_m^2)-\mathbb{E}(\mathbf{h}_m)^2=\mathbf{I}^{(1)}(\mathbf{z})\tag{14}
Var(hm)=E(hm2)−E(hm)2=I(1)(z)(14)
式中方差是通过观测值来计算,
I
\mathbf{I}
I表示重要度的集合。
如果选择对数似然函数作为误差函数
E
(
⋅
)
E(·)
E(⋅),则假设梯度估计为
h
x
=
∂
ln
p
(
x
;
z
)
∂
z
\mathbf{h}_{x}={\frac{\partial\ln p(x;\mathbf{z})}{\partial\mathbf{z}}}
hx=∂z∂lnp(x;z),借鉴信息论中的概念,得到:
V
a
r
x
(
h
)
=
E
x
{
h
x
h
x
T
}
=
J
(
h
)
(15)
\mathrm{Var}_x(\mathbf{h})=\mathbb{E}_x\left\{\mathbf{h}_x\mathbf{h}_x^T\right\}=J(\mathbf{h})\tag{15}
Varx(h)=Ex{hxhxT}=J(h)(15)
其中,
J
J
J为期望的Fisher信息矩阵(第五章重点讲)。我们得出结论,梯度的方差是梯度的外积的期望,并且等于期望的费雪信息矩阵。因此,所提出的度量
I
(
1
)
I^{(1)}
I(1)可以解释为方差估计和Fisher信息矩阵的对角线。
5 海森Hessian矩阵与Fisher信息量
5.1 Hessian矩阵
Hessian5矩阵存储了函数的二阶导数或偏微分信息,如
f
(
x
)
=
x
T
A
x
f(\mathbf{x})=\mathbf{x}^TA\mathbf{x}
f(x)=xTAx,其海森矩阵可以表示为
H
(
f
)
=
[
∂
2
f
∂
x
1
2
∂
2
f
∂
x
1
∂
x
2
⋯
∂
2
f
∂
x
1
∂
x
n
∂
2
f
∂
x
2
∂
x
1
∂
2
f
∂
x
2
2
⋯
∂
2
f
∂
x
2
∂
x
n
⋮
⋮
⋱
⋮
∂
2
f
∂
x
n
∂
x
1
∂
2
f
∂
x
n
∂
x
2
⋯
∂
2
f
∂
x
n
2
]
(16)
\mathbf{H}(f) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}\tag{16}
H(f)=
∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f
(16)
可以证明
H
(
f
)
=
A
+
A
T
\mathbf{H}(f)=A+A^T
H(f)=A+AT,Hessian矩阵可以用来对
f
(
x
)
f(\mathbf{x})
f(x)泰勒展开,比如
f
(
x
)
f(\mathbf{x})
f(x)在
x
=
a
\mathbf{x}=\mathbf{a}
x=a处泰勒展开
f
(
x
)
=
f
(
a
)
+
∑
i
=
1
n
∂
f
∂
x
i
(
a
)
(
x
i
−
a
i
)
+
1
2
!
∑
i
=
1
n
∑
j
=
1
n
∂
2
f
∂
x
i
∂
x
j
(
a
)
(
x
i
−
a
i
)
(
x
j
−
a
j
)
+
⋯
(17)
f(\mathbf{x}) = f(\mathbf{a}) + \sum_{i=1}^{n} \frac{\partial f}{\partial x_i}(\mathbf{a}) (x_i - a_i) + \frac{1}{2!} \sum_{i=1}^{n} \sum_{j=1}^{n} \frac{\partial^2 f}{\partial x_i \partial x_j}(\mathbf{a}) (x_i - a_i)(x_j - a_j) + \cdots\tag{17}
f(x)=f(a)+i=1∑n∂xi∂f(a)(xi−ai)+2!1i=1∑nj=1∑n∂xi∂xj∂2f(a)(xi−ai)(xj−aj)+⋯(17)
其中
1
2
!
\frac{1}{2!}
2!1哪一项后面就是Hessian矩阵。
5.2 Fisher信息量
Fisher信息量(Fisher Information)是统计学中的一个重要概念,度量了在一组观测数据中包含关于某个未知参数的信息量,简单来说,在一组观测数据中,Fisher信息量越大,对未知参数的估计就越准确。Fisher信息量在参数估计理论中扮演着核心角色,尤其是在评估估计量的效率方面。
对于一个随机变量
X
X
X和一个参数
θ
\theta
θ的概率密度函数(连续变量)或概率质量函数(离散变量)
p
(
x
∣
θ
)
p(x∣\theta)
p(x∣θ) ,Fisher信息量
I
I
I关于参数
θ
\theta
θ定义为
I
(
θ
)
=
−
E
[
∂
2
∂
θ
2
log
p
(
X
∣
θ
)
]
(18)
I(\theta) = -\mathbb{E}\left[ \frac{\partial^2}{\partial \theta^2} \log p(X | \theta) \right]\tag{18}
I(θ)=−E[∂θ2∂2logp(X∣θ)](18)
这里,
E
\mathbb{E}
E 表示期望值,第二项是关于
θ
\theta
θ的对数似然函数的二阶导数的期望值。
特点
Fisher信息量是非负的,它提供了关于参数估计的下界信息;Fisher信息量越大,表示观测数据提供关于参数 θ \theta θ 的信息越多,估计量越可靠;Fisher信息量可以用来评估估计量的性能,例如,Cramér-Rao不等式表明,对于无偏估计量,其方差至少为Fisher信息量的逆。
应用
1.参数估计:Fisher信息量可以用来评估参数估计量的效率,即估计量的方差下界。
2.模型选择:在模型选择中,如AIC(赤池信息量准则)和BIC(贝叶斯信息量准则)中,Fisher信息量的概念被用来衡量模型的拟合优度和复杂度。
3.统计推断:在构建置信区间和假设检验中,Fisher信息量可以提供关于参数不确定性的信息。
Cramér-Rao不等式
Cramér-Rao不等式是Fisher信息量的一个重要应用,它提供了无偏估计量方差的下界。对于无偏估计量
θ
^
\hat{\theta}
θ^,其方差
V
a
r
(
θ
^
)
\mathrm{Var}(\hat{\theta})
Var(θ^)至少为:
V
a
r
(
θ
^
)
≥
1
I
(
θ
)
(19)
\mathrm{Var}(\hat{\theta})\geq\frac{1}{I(\theta)}\tag{19}
Var(θ^)≥I(θ)1(19)
这意味着如果一个估计量的方差达到了Cramér-Rao下界,那么它被认为是效率最高的无偏估计量。
Fisher信息矩阵
Fisher信息矩阵(Fisher Information Matrix)是多元统计分析中的一个概念,它是对Fisher信息量的推广。当涉及到多个参数时,Fisher信息矩阵提供了一个多维参数空间中的信息度量。
假设我们有一个多参数的概率模型,其联合概率密度函数(连续变量)或概率质量函数(离散变量)为
p
(
x
∣
θ
)
p(x∣\theta)
p(x∣θ) ,
x
\mathbf{x}
x是观测向量,
θ
\boldsymbol{\theta}
θ是
k
k
k维参数向量,Fisher信息量
I
I
I关于参数
θ
\theta
θ定义为
I
(
θ
)
=
−
E
[
∂
∂
θ
log
p
(
X
∣
θ
)
⊙
∂
∂
θ
log
p
(
X
∣
θ
)
]
(20)
\mathbf{I}(\boldsymbol{\theta})=-\mathbb{E}\left[\frac\partial{\partial\boldsymbol{\theta}}\log p(\mathbf{X}|\boldsymbol{\theta})\odot\frac\partial{\partial\boldsymbol{\theta}}\log p(\mathbf{X}|\boldsymbol{\theta})\right]\tag{20}
I(θ)=−E[∂θ∂logp(X∣θ)⊙∂θ∂logp(X∣θ)](20)
⊙
\odot
⊙表示Hadamard积,即元素乘积如公式22。
fisher信息矩阵为
I
(
θ
)
=
[
I
11
(
θ
)
I
12
(
θ
)
⋯
I
1
k
(
θ
)
I
21
(
θ
)
I
22
(
θ
)
⋯
I
2
k
(
θ
)
⋮
⋮
⋱
⋮
I
k
1
(
θ
)
I
k
2
(
θ
)
⋯
I
k
k
(
θ
)
]
(21)
\mathbf{I}(\boldsymbol{\theta})=\begin{bmatrix}I_{11}(\theta)&I_{12}(\theta)&\cdots&I_{1k}(\theta)\\I_{21}(\theta)&I_{22}(\theta)&\cdots&I_{2k}(\theta)\\\vdots&\vdots&\ddots&\vdots\\I_{k1}(\theta)&I_{k2}(\theta)&\cdots&I_{kk}(\theta)\end{bmatrix} \tag{21}
I(θ)=
I11(θ)I21(θ)⋮Ik1(θ)I12(θ)I22(θ)⋮Ik2(θ)⋯⋯⋱⋯I1k(θ)I2k(θ)⋮Ikk(θ)
(21)
I
i
j
(
θ
)
I_{ij}(\theta)
Iij(θ)表示
θ
i
\theta_i
θi和
θ
j
\theta_j
θj之间的信息量:
I
i
j
(
θ
)
=
−
E
[
∂
∂
θ
i
log
p
(
X
∣
θ
)
∂
∂
θ
j
log
p
(
X
∣
θ
)
]
(22)
I_{ij}(\theta)=-\mathbb{E}\left[\frac\partial{\partial\theta_i}\log p(\mathbf{X}|\boldsymbol{\theta})\frac\partial{\partial\theta_j}\log p(\mathbf{X}|\boldsymbol{\theta})\right]\tag{22}
Iij(θ)=−E[∂θi∂logp(X∣θ)∂θj∂logp(X∣θ)](22)
在模型选择过程中,Fisher信息矩阵可以用来评估不同模型的性能。
reference
ShusenWang 2021 神经网络结构搜索 ↩︎
ICLR 2017 Neural architecture search with reinforcement learning ↩︎
ICML 2024 Differentiable Model Scaling using Differentiable Topk ↩︎
CVPR 2019 Importance Estimation for Neural Network Pruning ↩︎
弓长德帅97 2020 快速学懂Hessian矩阵 海森矩阵 ↩︎ ↩︎