21. 第21章算法分析

21. 算法分析

这个附录选自O'Reilly Media出版的Alen B.Downey的Think Complexity(2012)一书.
当你读完本书之后, 可能会像继续读读那本书.

'算法分析'是计算机科学的一个分支, 研究算法的性能, 尤其是他们的运行时间和空间需求.
参见http://en.wikipedia.org/wiki/Analysis_of_algorithms.

算法分析的实践目标是预测不同算法的性能, 以便于指导设计决策.

在2008年的美国总统大选中, 候选人巴拉克欧巴马在访问Google公司被要求做一个即兴分析.
Google的首席执行官埃里克•施密特问他: '给100万个32位整数排序的最高效率算法是什么'.
奥巴马显然被提示了, 因为它马上回答: '我觉得冒泡排序可能是错误的做法'. 
参见http://bit.ly/1MplwTf.

这是真的: 冒泡排序在概念上简单, 但对于大数据的排序很慢.
施密特想得到的答案可能是'基数排序'(http://en.wifipedia.org/wifiRadix_sort).
但如果你在面试时被问到这个问题, 我觉得更好的答案是: 
'给100万个数排序的最快算法应当是使用我用的语言提供的排序函数. 
它的性能应当对绝大数应用都足够好了, 但如果发现我的程序太慢,
我会使用一个性能分析器去查看时间花在哪里.
如果看起来更快的排序算法带来明显的提升, 那我会去寻找一个基数排序的良好实现.'

算法分析的目是在不同算法间做出有意义的比较, 但也有一些问题.
* 算法的相对性可能依赖于硬件的特征, 所以一个算法可能在机器A上更快, 另一个在机器B上更快.
  这个问题的通用解决方法是先指定一个'机器模型', 
  并分析在一个指定的机器模型中一个算法需要执行的步骤或操作.

* 相对性能还可能依赖于数据集的细节特征.
  例如, 有的排序算法在数据已经是部分排序的情形下比其他算法更快, 有的程序在这种情况下反而慢.
  避免这个问题的通常办法是分析'最坏情况'场景.
  有的时候分析平均情况的性能也有用, 但也通常会更难, 因为有哪些情形可以用来'平均'往往并不明显.

* 相对性能也依赖于问题的规模. 
  对小序列更快的排序算法可能对大序列就慢了. 
  这个问题的通常解决方案是用一个问题规模的函数来表达运行时间(或操作数), 
  并根据问题规模增法的速度将函数进行归类.
  

这种比较的好处之一是自然而然地可以将算法进行简单地分类.
例如, 我知道算法A的运行时间趋向于和输入的规模n成比例, 而算法B趋向于和n^2成比例,
那么我会预期至少对应大的n值, 算法A比算法B块.
这种分析也有需要注意的地方, 后面会谈到.

21.1 增长量级

假设你需要分析两个算法, 并依照输入的规模来表达它们的运行时间:
算法A需要100n + 1步来解决规模为n的问题, 算法B需要n^2 + n + 1 步.

下面的表格显示了这两个算法在不同的问题规模下的运行时间:

输入规模	算法A的运行时间	算法B的运行时间
10	1 001	111
100	10 001	10 101
1 000	100 001	1 001 001
10 000	1 000 001	>10**10

ps:
'首项'是一个多项式中最高次方的项. 

在一个多项式中, 每一项都由一个系数和一个指数幂次的变量组成.
例如, 在多项式 3x^2 + 2x + 1 中, 3x^2, 2x和1都是多项式的项.

系数: 是指代数式的单项式中的数字因数, 比如说代数式"3x",
它表示一个常数3与未知数x的乘积, 我们把3叫做这个代数式的系数, "叫做常数项.

"非首项"指的是在一个多项式中, 除了第一项之外的所有项.
在上面的例子中, 非首项是2x和1.

非首项通常在多项式运算中非常重要, 因为在对多项式进行加减乘除等操作时,
我们通常只需要考虑它们的非首项, 这是因为多项式的首项通常对结果的影响最大,
并且在对多项式进行操作时往往可以简化计算.

在n=10时, 算法A看起来很差; 它几乎需要10倍于算法B的时间.
但对于n=100来说它们就已经差不多了, 而在更大的规模时, 算法A远好于算法B.

这里根本的原因在于对很大的n值, 任何包含n^2项的函数都会比首项是n的函数增长快速很多.

对于算法A, 首项有一个很大的系数100, 因此算法B在小的n时比算法A快.
但不论系数是多少, 总有一个n值会导致an^2 > bn.

对于非首项来说也如此. 即使算法A的运行时间是n+1000000, 对于足够大的n, 任然会比算法B快.
(非首项, 我数学不好看不懂了, )

总的来说, 我们预期有更小的首项的算法对大规模问题来说是更好的算法.
但对于小一些的问题来说, 可能存在一个'交叉点', 那里其他算法可能更好.
交叉点的位置取决于算法的细节, 输入已经硬件的条件, 所有在想法分析时常常被忽略掉.
但那并不意味着你可以忘记它.

如果有两个算法有相同的首项, 则很难说哪一个更好; 同样的, 答案也取决于细节.
所以对于算法分析来说, 首项相同的函数被认为是同等的, 即使他们的系数不同.

'增长量级'就是各种增长行为是同等的函数的集合.
例如, 2n, 100n和n+1都是一个增长量级, 用'大O标记法'写作O(n), 通常称为'线性的',
因为这个集合中的每个函数都依据n线性增长.

所有首项是n^2的函数都属于O(n^2), 它们被称为是'平方的'.

下面的表格显示了算法分析中大部分最常见的增长量级, 按照更坏的程序递增:

增长量级	名称
O(1)	常量级
O(logbn)	对数级(对任意b)
O(n)	线性级
O(nlogbn)	nlogn
O(n^2)	平方级
O(n^3)	立方级
O(c^n)	指数级(底数c任意)

对应对数项, 底数并没有影响; 修改底数相当于乘以一个常量, 而那样并不影响增长量级.
类似地, 所有的指数函数都是同一个增长量级, 不论指数级是什么.
指数函数增长非常迅速, 所以指数级算法只在小规模的问题中应用.

1. 练习1

在http://en.wikipedia.org/wiki/Big_O_notation上阅读大O标记法的维基百科页面, 并回答下列问题.
* 1. n^3 + n^2的增长量级是多少, 1000000n^3 + n^2呢? n^3 + 1000000n^2呢?

n^3 + n^2 的增长量级是 O(n^3)

1000000n^3 + n^2 的增长量级是 O(n^3)

n^3 + 1000000n^2 的增长量级是 O(n^3)

对于第一个算法, 随着输入规模 n 的增大, n^3 的增长速度比 n^2 更快, 
因此可以忽略 n^2 对总体复杂度的影响, 算法的时间复杂度为 O(n^3). 

对于第二个算法, 1000000n^3 的增长速度比 n^2 更快, 
因此可以忽略 n^2 对总体复杂度的影响, 算法的时间复杂度为 O(n^3). 

对于第三个算法, n^3 的增长速度比 1000000n^2 更快, 
因此可以忽略 1000000n^2 对总体复杂度的影响, 算法的时间复杂度为 O(n^3).

* 2. (n^2 + n)•(n + 1)的增长量级是多少? 在相乘之前, 请记住你只需要首项.

在进行乘法运算之前, 我们可以将 (n^2 + n) 和 (n + 1) 展开, 得到:
(n^2 + n) • (n + 1) = n^3 + n^2 + n^2 + n = n^3 + 2n^2 + n

因此, (n^2 + n) • (n + 1) 的增长量级是 O(n^3). 
在求增长量级的过程中, 我们只需要保留式子中的最高次项, 即 n^3, 忽略其他低阶项和常数项.

* 3. 如果f是O(g), 对于未指定的函数g, 我们怎么说af+b?

如果 f 是 O(g), 其中 g 未指定函数, 则对于任意常数 a 和 b, 函数 af+b 的增长量级仍然是 O(g).

* 4. 如果f1和f2都是O(g), 那么f1+f2呢?

如果 f1 和 f2 都是 O(g), 则 f1+f2 的增长量级仍然是 O(g). 
这是因为在 f1 和 f2 的增长量级相同时, 它们的和的增长量级也相同.

* 5. 如果f1是O(g)而f2是O(h), 那么f1+f2呢?

如果 f1 是 O(g) 而 f2 是 O(h), 则 f1+f2 的增长量级取决于 g 和 h 的相对增长速度.
如果 g 的增长速度比 h 快, 那么 f1 的增长将主导 f1+f2 的增长, 
因此 f1+f2 的增长量级为 O(g). 如果 h 的增长速度比 g 快, 
那么 f2 的增长将主导 f1+f2 的增长, 因此 f1+f2 的增长量级为 O(h). 
如果 g 和 h 的增长速度相同, 则 f1+f2 的增长量级为 O(g) 或 O(h).

* 6. 如果f1是O(g)而f2是O(h), 那么f1•f2呢?

如果 f1 是 O(g) 而 f2 是 O(h), 则 f1•f2 的增长量级为 O(g•h). 
这是因为 f1 和 f2 的增长量级分别是 g 和 h, 因此 f1•f2 的增长量级为 g•h.

关心程序性能的程序员常常会觉得这种分析很难理解.
它们有道理: 有时候系数和非首项也能带来不同.
有时候硬件的细节. 编程语言, 以及输入的特征, 都能带来很大的区别.
并且对应小规模问题来说, 渐进行为是无关紧要的.

但如果在闹钟记着这些需要注意的要点的话, 算法分析毕竟是一个有用的工具.
至少对于大规模问题来说, '更好'的算法往往确实更好, 并且有时候它会好的多.
两个增长量级相同的算法的区别往往是一个常量值, 但一个好算法和一个坏算法的差距是没有界限的!

21.2 Python基本操作的分析

在Python中大部分算法操作都是常量时间的;
乘法通常比加法和减法花费更多的时间, 而除法花费的时间更多, 但这些操作的时间与参数大小无关.
特别大的整数是一个例外, 在哪种情况下, 运行时间随数字的位数增加而增加.

索引操作-在序列或字典中写入元素-也是常量时间的, 与数据结构的规模无关.

遍历一个序列或字典的for循环通常是线性的, 只要循环体内的操作本身是常量级.
例如, 将一个列表的元素相加时线性的:

total = 0
for x in t:
	total += x

内置函数sum也是线性的, 因为它做相同的事情. 但它趋向于更快些, 因为实现得更高效.
用算法分析的语言来说, 就是它有一个更小的首项系数.

作为一个经验规则, 如果循环体的增长量级是O(n^2)则整个循环时是(n^(a+1)).
例外情况是当你能够证明循环在一个常量数的迭代之后就能退出.
如果不论n是多少, 循环只最多运行k次, 则即使对很大的k来说, 整个循环的增长级还是O(n^a).

乘以k并不会改变增长量级, 而除法也不会.
所以, 如果一个循环体的增长量级是O(n^a), 那么它运行n/k次, 
即使对很大的k来说, 整个循环的增长量及也任然是O(n^(a+1)).

大部分字符串和元组操作时线性的, 只有下标访问和len函数例外, 它们是常量级时间的.内置函数min和max是线性的.
切片操作的运行时间与输出的长度成正比, 而与输入的长度无关.

字符串拼接是线性的, 它的运行时间以操作数的长度的总和有关.

所有的字符串方法都是线性的, 但如果字符串的长度受限于一个常量(例如, 在只有一个字符串的字符串的操作),
可以看作是常量的. 字符串方法join是线性的, 它的运行时间与字符串的总长度有关.

大多数列表方法是线性的, 但也有一些例外.
* 在列表结尾处添加一个元素的操作平均来说是常量时间的; 当它空间不足时, 偶尔会复制到另一个更大的地方.
  但总的n次操作的时间量级是O(n), 所以每次操作的平均时间是O(1).

* 从列表结尾删除一个元素的操作是常量时间的.

* 排序的量级是0(nlogn).
  大部分字典操作和方法都是常量时间的, 但也有一些例外.
  
* update的运行和作为参数传入的字典的大小成正比, 而不是被更新的字典本身.

* keys, values和items都是常量时间, 因为它们返回的迭代器.
  但是, 如果循环遍历这个迭代器, 则循环时线性的.
 
字典的效率是计算机科学的一个小奇迹. 我们会在21.4节中介绍它是如何工作的.

1. 练习2

在http://en.wikipedia.org/wiki/Sorting_algorithm阅读排序算法的维基百科页面并回答下列问题.

* 1. 什么是'比较排序'?, 比较排序的最坏情况的增长量级最好是什么?
     任意排序算法中, 最坏情况的增长量级最好是多少?

比较排序是通过比较元素之间的大小关系来排序的算法. 
最坏情况的增长量级最好是 O(nlogn). 对于任意排序算法来说, 最坏情况的增长量级最好也是 O(nlogn).

* 2. 冒泡排序的增长量级是多少? 为什么奥巴马认为它是'错误的做法'?

冒泡排序的增长量级是 O(n^2). 
奥巴马认为它是错误的做法是因为它的时间复杂度太高, 而且在大多数情况下, 它的表现都比其他排序算法要差.

* 3. 基数排序的增长量级是多少? 要使用它, 我们需要哪些前置条件?

基数排序的增长量级是 O(dn), 其中 d 是数字的位数. 要使用基数排序, 需要满足以下前置条件：

a. 元素是可以分解为整数位的数字的形式. 
b. 元素之间有明确的大小关系. 
c. 要排序的元素的范围不是很大.

* 4. 稳定排序是什么? 为什么在实践中它很重要?

稳定排序是指在排序过程中, 如果有两个元素相等, 那么它们在排序后的序列中相对位置不会改变. 
在实践中, 稳定排序非常重要, 因为它可以保留原始数据中的排序关系, 避免在排序后失去数据的有用信息.

* 5. 最差的(有名字的)排序算法是什么?

最差的排序算法是 bogosort, 也称为 stupid sort 或者 permutation sort. 
它的时间复杂度是 O(n*n!), 因此在大多数情况下, 它的表现都非常糟糕.

* 6. C语言库里用的排序算法是什么? Python里用的是什么? 这些算法稳定吗?
     你可能需要去Google搜索这些答案.

在 C 语言库中, 常用的排序算法是 quicksort、mergesort 和 heapsort. 在 Python 中, 常用的排序算法是 timsort, 它结合了 mergesort 和 insertion sort 的思想. 这些算法都是稳定的.

* 7. 很多非计较排序都是线性的, 那么为什么Python会使用O(nlogn)的比较排序呢?

许多非比较排序算法都是线性的, 但它们通常具有比较严格的前置条件, 只能用于特定类型的数据. 
而比较排序算法则适用于所有类型的数据, 并且在大多数情况下表现都很好. 
因此, Python 使用 O(nlogn) 的比较排序算法, 以便能够应对各种情况下的排序需求.

21.3 搜索算法的分析

搜索是一种算法, 接收一个集合和一个目标元素, 并决定这个元素是否在集合中, 通常返回元素的索引.

最简单的搜索算法是'线性搜索', 即按顺序遍历集合的每一个元素, 直到找到目标元素为止.
在最坏的情况下, 它会遍历整个集合, 所以运行时间是线性的.

序列的in操作符使用一个线性搜索; 字符串方法find和cound也是这样的.

如果序列中的元素是排好的, 可以使用'二分查找', 它的增长量级是O(log n).
二分法查找和在字典(真实的字典, 而不是那个数据结构)中查找单词的算法类似.
不想普通搜索那样从第一个元素开始, 它是从序列的中间开始, 检查查找的词是在中间的元素之前还是之后.
如果在之前, 则继续查找序列的前半段, 否则查找后半段.
不论哪种情况, 都可以将查找的数量减少一半.

如果序列有1 000 000个元素, 大概需要花20个步骤找到单词或者发现它不存在.
所有那样会比线性查找快大概50 000倍.

二分查找可以比线性查找快很多, 但需要序列本身是排好序的, 也就需要一些额外工作.
有另一个数据结构, 称为散列表(hashtable), 它甚至更快-它可以用常量时间来搜索-而不需要元素是排好序的.
Python字典是使用散列表实现的, 因此大部分字典操作, 包括in操作符, 都是常量时间的.

21.4 散列表

为了解释散列表的工作机制以及为何它的效率如此好, 我们先从一个简单的映射实现开始,
并逐步改善它, 直到成为一个散列表.

我使用Python来展示这些实现. 但真实世界中, 你不需要用Python写这样的代码, 你只需要直接使用字典即可!
所有本章中剩下的本分, 你需要想要字典并不存在, 而你需要实现一个数据结构将键隐射到值.
你需要实现的操作有以下几个.

add(k, v)

添加一个新项, 将键k映射戴值v.
在Python字典d中, 这个操作写在d[k] = v,

get(k)

根据键k查找对应的值. 在Python字典d中, 这个操作写作d[k]或d.get(f).
就现在来说, 我假设每个键只出现一次. 最简单的实现是使用一个元组列表, 每个元组是一个键值对:

class LinearMap:
    def __init__(self):
        self.items = []

    def add(self, k, v):
        self.items.append((k, v))


def get(self, k):
    for key, val in self.items:
        if key == k:
            return val
    raise KeyError

add往元组列表中添加一项, 这个操作是常量时间的.

get使用一个for循环来搜索列表: 如果找找了目标, 则返回对应的值; 否则抛出KeyError. 所有get是线性的.

另一个方案是让列表按照键来排序. 这样get就可以使用二分法查找, 其增长量级是O(logn).
但插入一个新项到列表中间是线性的, 所以这可能也不是最好的选择.
也有数据结构可以用对数时间好, 所有我们继续.

改善LinearMap的方法之一是将键值对的列表拆分成更小的列表.
下面是一个称为BetterMap的实现, 它是一个包含100个LinearMap的列表.
我们接下来会看到, get的增长量级仍然是线性的, 但是BetterMap散列表更近一步.

class BetterMap:
    def __init__(self, n=100):
        self.maps = []
        for i in range(n):
            self.maps.append(LinearMap())

    def find_map(self, k):
        index = hash(k) % len(self.maps)
        return self.maps[index]

    def add(self, k, v):
        m = self.find_map(k)
        m.add(k, v)

    def get(self, k):
        m = self.find_map(k)
        return m.get(k)

# 线性映射
class LinearMap:
    # 初始化方法, 设置items属性为一个列表
    def __init__(self):
        self.items = []

    # 往列表中, 添加元组(k键, v值)
    def add(self, k, v):
        self.items.append((k, v))

    # 通过k键获取v值
    def get(self, k):
        # 遍历列表, 得到一个元组, 将元组分散赋值给key, val.
        for key, val in self.items:
            # key 为 k时返回val.
            if key == k:
                return val

        # 遍历结束, 都没找则说明键不存在
        raise KeyError


# 更好的映射
class BetterMap:
    # 初始化方法
    def __init__(self, n=100):
        # 隐射列表
        self.maps = []
        # 遍历0-99
        for i in range(n):
            # 实例100个线性映射对象, 并添加到隐射列表中
            self.maps.append(LinearMap())

    # 查找隐射
    def find_map(self, k):
        # hash(k)值 每次都不同, 对len(self.maps)求余数, 保证它的余数在len(self.maps)-1之间.
        # x % 100 保证 index的值在0-99中.
        index = hash(k) % len(self.maps)
        # 好奇就查看一眼
        print('key的哈希值:%s \nindex的值:%s' % (hash(k), index))
        # 索引取值, 值时一个 线性映射对象
        return self.maps[index]

    # 添加键值
    def add(self, k, v):
        # 按k计算索引, 并返回索引对应的 线性映射对象
        m = self.find_map(k)
        # 线性映射对象执行add方法往items列表中添加值.
        m.add(k, v)

    # 获取值
    def get(self, k):
        # 按k计算索引, 并返回索引对应的 线性映射对象
        m = self.find_map(k)
        # 线性映射对象执行get方法往items列表中取值.
        return m.get(k)


obj = BetterMap()
obj.add('k1', 'v1')
res = obj.get('k1')
print(res)
"""
key的哈希值:-111025584990275242 
index的值:58
key的哈希值:-111025584990275242 
index的值:58
v1

"""

__init__创建有n个LinearMap组成的列表.
find_map被add和get调用, 用来确定用哪个映射来保存新项, 或者到哪个映射里去搜索.

find_map使用内置函数hash, 它接收几乎所有的Python对象, 并返回一个整数.
这个实现的限制之一是它只对可散列的键类型可以.
可变类型, 如列表的和字典, 是不可散列的.

两个认为相等的可散列对象会返回相同的散列值, 
但反过并不一定是真: 两个具有不同值的对象可以返回相同的散列值.

find_map使用求余操作符来将散列值封装到0到len(self.maps)的范围中, 这样结果是列表的一个合法索引.
当然, 这意味这很多不同的散列值会封装到用一个索引上.
但如散列函数将对象分配地很均匀(这也是散列表函数设计的目标), 那么我们预计每个LinearMap有n/100个项.

因为LinearMap.get的运行时间是和其包含的项数成正比的, 所以我们预计BetterMap会比LinearMap快100倍.
增长量级仍然是线性, 但首项系数更小. 这很好, 但仍然不如散列表好.

下面(终于)是让散列表能变快的光键原因: 如果你能保证LinearMap的长度有限, LinearMap.get则会是常量时间.
你需要做的只是记录元素的总数, 并当每个LinearMap的大小超过一个阈值时, 
重新划分散列表, 添加更多的LinearMap.
下面是一个散列表的实现:

# 哈希映射
class HashMap:
    # 初始化方法
    def __init__(self):
        # 生成一个BetterMap对象, 它包含两个LinearMap对象(参数2产生的).
        self.maps = BetterMap(2)
        # 计算器
        self.num = 0

    # 通过k获取值
    def get(self, k):
        return self.maps.get(k)

    # 添加键值
    def add(self, k, v):
        # 当num属性的值等于 LinearMap的items列表的值, 则调整隐射对象
        if self.num == len(self.maps.maps):
            self.resize()
		
        # 否则, 添加键值到新的隐射对象中
        self.maps.add(k, v)
        # 计数加1
        self.num += 1

    # 调整
    def resize(self):
        # 新的映射对象
        new_maps = BetterMap(self.num * 2)
        # 遍历BetterMap对象中的列表
        for m in self.maps.maps:
            # 遍历列表中的元组, 分散赋值给k, v
            for k, v in m.items:
                # 将旧的隐射对象, 保存到新的隐射对象中.
                new_maps.add(k, v)

        # 替换映射集合
        self.maps = new_maps

每个HashMap都包含一个BetterMap__init__从2个LinearMap开始, 并初始化num, 它会用来记录总的项数.

get只需要分配到对应的BetterMap. 真正的工作都发生在add中, 它会检查项数和BetterMap的大小:
如果相等, 那么每个LinearMap的平均项数是1, 所以它调用resize.

resize创建一个新的BetterMap, 比之前大一倍, 并将旧有的映射中的项'重新散列'到新的映射中.

重新散列时有必要的, 因为LinearMap的数量的改变, 导致find_map的求余操作的分母改变.
也就是说, 有些原先会散列到用一个LinearMap的项会分配到不同的LinearMap中(这也是我们想要的, 对吧?)

重新散列时线性的, 所以resize是线性的, 看起来可能不好, 因为我保证过add应当是常量时间的.
但请记得我们并不是每次都需要进行resize, 所有add通常是常量时间的, 只是偶尔会线性.
add运行n次的总时间和n成正比的, 因此每次调用add的平均时间是常量时间!

要明白散列表如何工作, 考虑从一个空的HashTable开始, 并添加一些项.
我们从2个LinearMap开始, 所有最开始两个add会很快(不需要resize).
我们说它们每次花费一单位的工作量. 下一个add会需要resize, 所有我们需要重新散列前两项
(我们说着需要再加2个单位的工作量)并添加一个新项(再加1个单位).
再添加一项花费1单位, 所以至今为止是4项, 花费了6个单位的工作.

下一个add需要5个单位, 但接着的3个都只需要1个单位, 所以总共是8项花费了14单位.
再下一个add需要9个单位, 但接着我们可以在再次resize之前添加7项, 所以总和是16个add花费了30单位.

在32个add时, 总共的花费是62单位, 为我希望你已经开始看到其中的模式了.
在n个add之后, 假设n是2的乘方, 总得花费是2n-2单位, 所以平均每个add的工作量是稍微小于2个单位的.
当n是2的乘方时, 这是最好情况; 对于其他的n值, 平均工作量稍高一点, 但这并不重要. 重要的是这是O(1).

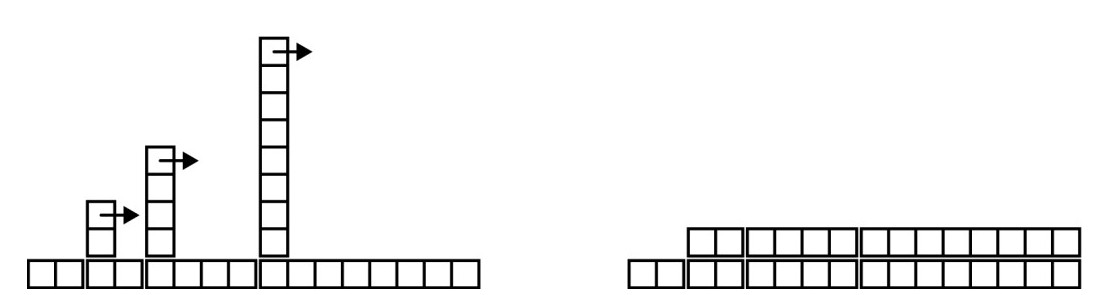
下图(散列表add的消耗)用图形画的方式展示了这个过程. 每个方块代表一个单位的工作量.
每一列显示每个add的工作量: 从左到右, 前两个add花费1单位, 第三个花费3单位, 等等.

_gallerySharetemp.png (2)

多余的重新散列表的工作看起来像一序列不断增高的塔, 之间的间隔越来越远.
现在如果你将塔推倒, 将resize的花费均摊到所有add操作上, 就会发现n个add之后总的花费是2n-2.

这个算法的一个重要特点是当我们调整HashTable的大小时, 它会几何增长; 也就是, 我们乘以一个常量到大小上.
如果算术地增加大小-每次添加固定数量的数-那么每个add的平均时间是线性的.

可以从↓下载我的HashMap实现, 但请记住并没有使用它的理由. 如果需要一个映射, 直接使用Python字典即可.
https://github.com/AllenDowney/ThinkPython2/blob/master/code/Map.py

21.5 术语表

算法分析(analysis of algorithms): 通过对比运行时间以及/或者空间需求来对比算法的方法．

机器模型(machine model): 用于描述算法的简化的计算机表示形式.

最坏情况(worst case): 让指定算法运行最慢(或者需要最多空间的)的输入.

首项(leading term): 在多项式中, 指数最高的项.

交叉点(crossover point): 两个算法需要相同的运行时间或空间的问题规模.

增长量级(order of growth): 在算法分析时, 如果我们认为一组函数的增长速度可以看作相等,
	则将这组函数称为同一个增长量级的. 例如, 所有线性增长的函数都属于同一个增长量级.
	
大O标记法(Big-Oh notation): 表示增长量级的方法. 例如, O(n)表示所有线性增长的函数集合.

线性(linrat): 运行时间和问题规模(至少对于大规模来说)成正比的算法.

平方量级(quadratic): 运行时间和n^2成正比的算法, 其中n指的是问题规模.

搜索(search): 定位集合(如列表和字典)中某个元素或者判定它不在其中的问题.

散列表(hashtable): 一种表示键值对集合且搜索时常量级的数据结构.

译后记

<<像计算机科学家一样思考>>这一系列数, 早有耳闻, 他可谓开创了程序设计入门书的一个新思路.
授人以鱼, 不若授人以渔; 教人编程, 不如引导人思考; 教人语言细节, 不若指明语言精要.
而结合Python语言之后, 得到的<<项计算机科学家一样思考Python>>这本书, 
则是在这个思路上走到一个极致的佳作.

我是工作之后才开始接触Python的.
在那之前一直使用C/C++, java, C#等传统风格的语言, 再看到Python, 不免有耳目一新之感.
为何以往觉得晦涩难懂的程序设计理念, 在Python中却表达得这么简单易懂?
为何以往需要绞尽脑计才能拼出来的大段代码, 在Python里却只需要几个简单调用即可?
为何繁杂的集合操作, 在Python中却只需要一个行列表理解循环语句就完成了?
为何Python的文档那么容易找, 还可以使用交互模式轻松尝试?
每次使用Pyhton编写程序之后, 总会感慨, 当初初学程序设计语言的时候, 如果教的是Python该多好.
想信所有学过C/C++之后再接触Python这类语言的任, 都会有相同的感受吧.

那么是什么原因让C/C++几乎垄断了程序设计语言的教材呢? 我觉得更多的是历史惯性.
在计算机科学教育开始普及的20世纪70, 80年代, C语言正在其鼎盛时期, 几乎所有的人都在用C开发程序,
软件, 游戏几乎都是用C甚至汇编开法的.
硬件性能的限制, 让那些更抽象, 更高阶的语言, 无法普及开来. 因此教学自然也使用它.
久而久之形成了惯性, 到了新世纪, 程序设计的教学已经搞不上语言发展的潮流了.
我们的程序越来越复杂, 越来越像人脑, 而教学的语言任然在使用高级语言中最贴近机器的C.
而C++, Java, C#, 虽然相对于C更抽象高阶, 但由于这些语言设计的初衷仍是以拓展C为主,
所有不过是在这一惯性上多走了五十步而已.

本书正是扭转这种矛盾局面的一个有益的尝试. 
<<像计算机科学家一样思考>>是对程序设计教学模式的真谛的领悟, 而使用Python这种简洁强大的高阶语言,
而使用Python这种简洁强大的高阶语言, 也正是这种思路最贴切的贯彻.
授人以渔, 自然应当用最好的渔具; 引导人思考, 当然也应使用更贴近人的思路而不是机器思路的语句.
Python在高阶语言中, 是一个从理念和实际综合考量后非常合适的候选.