题目
对随机变量![]() 的随机性的一个度量是它的熵(entropy),熵定义为:
的随机性的一个度量是它的熵(entropy),熵定义为:
![]()
如果![]() ,求这个熵,并说明它与PDF集中度的关系。观察到数据后,后验PDF的熵可以确定为:
,求这个熵,并说明它与PDF集中度的关系。观察到数据后,后验PDF的熵可以确定为:
![]()
且它应该比![]() 小。因此,通过观察得到的信息的度量是:
小。因此,通过观察得到的信息的度量是:
![]()
证明![]() 。在什么条件下,
。在什么条件下,![]() ?
?
提示:把![]() 表示为:
表示为:
![]()
另外,对于PDF ![]() ,
, ![]() ,需要不等式:
,需要不等式:
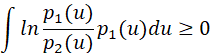
当且仅当![]() 时,等式成立。
时,等式成立。
解答:
![]()
所以:
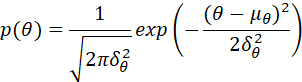
因此:
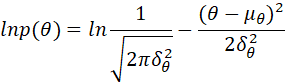
所以:
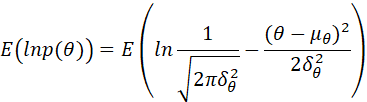
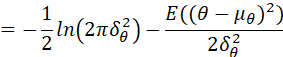
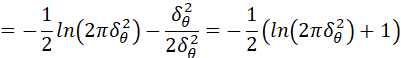
最终得到:
![]()
由题目条件,PDF约集中,也即是![]() 越小,此时对应的
越小,此时对应的![]() 也就越小。换句话说,熵大的信号,具有较大的
也就越小。换句话说,熵大的信号,具有较大的![]() ,或者
,或者![]() 越随机。
越随机。
接下来求条件概率下的信息度量,因为:
![]()
![]()
![]()
所以:
![]()
![]()
![]()
![]()

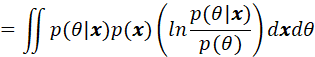
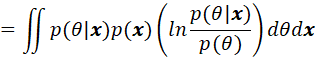
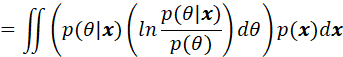
其中利用
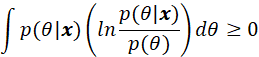
所以,当![]() 为概率密度,且也非负时,得到
为概率密度,且也非负时,得到
![]()
而上式积分为零的条件得到:
![]()
也就表示此时![]() 和
和![]() 独立,此时
独立,此时![]() ,也就是后验概率和先验概率一致,此时没有提供额外的信息。
,也就是后验概率和先验概率一致,此时没有提供额外的信息。
另外一个维度,如果![]() ,此时
,此时![]() ,也即是
,也即是![]() 此时一定比
此时一定比![]() 小,换句话说,
小,换句话说,![]() 估计的
估计的![]() 就越集中,也就是MMSE估计量具有更小的方差。
就越集中,也就是MMSE估计量具有更小的方差。









![P1002 [NOIP2002 普及组] 过河卒](https://img-blog.csdnimg.cn/img_convert/16a7e8fa0c1055f9d777242d77a913dd.png)