图像处理：图像清晰度评价

news2025/7/9 5:58:17

0、实现效果

1、概述

2、模糊度分类

1、运动模糊

2、压缩模糊

3、高斯模糊

3、清晰度量化指标

Brenner

能量梯度函数(Energy of Gradient)

编辑

Roberts

Laplace

SMD（灰度方差）函数

SMD2 （灰度方差乘积）函数

4、图像清晰度评价实现

5、总结与评价

参考资料：

0、实现效果

能够通过一张标准图，对同一组相机拍摄的照片进行清晰度评价。

1、概述

图像清晰度是用来指导调焦机构找到正焦位置的评价函数。理想的清晰度评价曲线类似于泊松分布，请看下图：

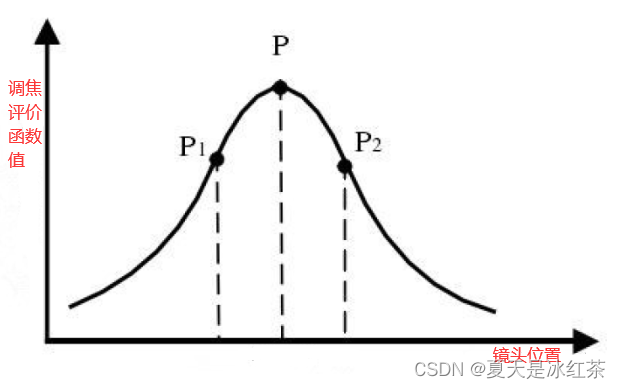
p点对应于正焦位置，P1 和P2 为正焦位置焦前和焦后采集到图像的清晰度评价结果。

正焦的图像比模糊的离焦图像边缘要更加的锐利清晰，相应的边缘像素灰度值变化大，因而会有更大的梯度值，从数学的角度来看图像，它是二维的离散矩阵，利用梯度函数可获取图像的灰度信息，来判别图像的清晰度，在离散信中梯度表现为差分形式。

2、模糊度分类

1、运动模糊

运动模糊是在捕获图像时，快门在打开时间内成像系统和拍摄对象的短暂相对运动，造成成像在某个方向上形成的模糊。

2、压缩模糊

压缩模糊是图像在进行有损压缩丢失部分信息。

3、高斯模糊

高斯模糊是人为引入的一种模糊，使用高斯低通滤波器对原始图像进行滤波得到的。

3、清晰度量化指标

Brenner

Brenner梯度函数是最简单的梯度评价函数，它只是简单的计算相邻两个像素灰度差的平方，该函数定义如下：
$D(f)=\sum_{y} \sum_{x}\left | f(x+2,y)-f(x,y)\right |^{2}$

f(x,y) 表示图像f对应像素点(x,y)的灰度值，D(f)为图像清晰度计算结果。

python实现：

def brenner(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shapes = np.shape(img)
    output = 0
    for x in range(0, shapes[0]-2):
        for y in range(0, shapes[1]):
            output+=(int(img[x+2,y])-int(img[x,y]))**2
    return output

能量梯度函数(Energy of Gradient)

将 x 方向和 y 方向的相邻像素的灰度值之差的平方和作为每个像素点的梯度值，对所有像素梯度值累加作为清晰度评价函数值，表达式如下所示：

$D(f)=\sum_{x} \sum_{y}\left \{[f(x+1,y)-f(x,y)]^{2}+[f(x,y+1)-f(x,y)]^{2}\right \}$

python实现：

def EOG(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shapes = np.shape(img)
    output = 0
    for x in range(0, shapes[0]-1):
        for y in range(0, shapes[1]-1):
            output+=((int(img[x+1,y])-int(img[x,y]))**2+(int(img[x,y+1])-int(img[x,y]))**2)
    return output

Roberts

Roberts函数与能量梯度函数相似，它是利用对角方向像素点灰度值之差。将4个相邻像素点的灰度值交叉相减的平方和作为每个像素点的梯度值，对所有像素梯度值累加作为清晰度评价函数值，表达式如下式所示：

$D(f)=\sum_{x} \sum_{y}\left \{[f(x+1,y+1)-f(x,y)]^{2}+[f(x+1,y)-f(x,y+1)]^{2}\right \}$

python实现：

def Roberts(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shapes = np.shape(img)
    output = 0
    for x in range(0, shapes[0]-1):
        for y in range(0, shapes[1]-1):
            output+=((int(img[x+1,y+1])-int(img[x,y]))**2+(int(img[x+1,y])-int(img[x,y+1]))**2)
    return output

Laplace

采用Laplace算子与图像各个像素点的灰度值进行卷积得到一个梯度矩阵记为 $G(x,y)$ ，取各像素点梯度的平方和作为评价函数，如下式所示：

$D(f)=\sum_{x} \sum_{y}\textit{G}^{2}(x,y)$

$\textit{G}(x,y)=f(x,y)\otimes L$

$L=\begin{bmatrix} 0& 1 & 1\\ 1 & -4&1 \\ 0 & 1& 0 \end{bmatrix}$

python实现：

def Laplacian(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    return cv2.Laplacian(img,cv2.CV_64F).var()

由于之前推导过，你可以查看此文，这是我以前所写的一篇博客:(2条消息) 图像处理：边缘检测原理_夏天是冰红茶的博客-CSDN博客

SMD（灰度方差）函数

当完全聚焦时，图像最清晰，图像中的高频分量也最多，故可将灰度变化作为聚焦评价的依据，灰度方差法的公式如下：

$D(f)=\sum_{y} \sum_{x}(\left |f(x,y)-f(x,y-1) \right |+\left |f(x+1,y)-f(x,y) \right |)$

python实现：

def SMD(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shape = np.shape(img)
    output = 0
    for x in range(1, shape[0]-1):
        for y in range(0, shape[1]):
            output+=math.fabs(int(img[x,y])-int(img[x,y-1]))
            output+=math.fabs(int(img[x,y]-int(img[x+1,y])))
    return output

SMD2 （灰度方差乘积）函数

SDM函数具有较好的计算性能，但其缺点也很明显，即在焦点附近灵敏度不高，即该函数在极值点附近过于平坦，从而导致聚焦精度难以提高。在《一种快速高灵敏度聚焦评价函数》中李郁峰等人在论文中提出了一种新的评价函数，称之为灰度方差乘积法，即对每一个像素领域两个灰度差相乘后再逐个像素累加，该函数定义如下：

$D(f)=\sum_{y} \sum_{x}(\left |f(x,y)-f(x+1,y) \right |*\left |f(x,y)-f(x,y+1) \right |)$

python实现：

def SMD2(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像约清晰越大
    '''
    shape = np.shape(img)
    output = 0
    for x in range(0, shape[0]-1):
        for y in range(0, shape[1]-1):
            output+=math.fabs(int(img[x,y])-int(img[x+1,y]))*math.fabs(int(img[x,y]-int(img[x,y+1])))
    return output

4、图像清晰度评价实现

SWD2:

import cv2
import pyps.pyzjr.definition as din
import pyps.pyzjr.utility as ult


image=ult.read_resize_image("./compare/8881.jpg",space=True)
img = din.SMD2(image)
print(img)

cv2.putText(image, f"definition:{img:.2f}", (10, 30),
            cv2.FONT_HERSHEY_SIMPLEX, 0.8, (0, 0, 255), 3)
cv2.imshow("definition_Image", image)

cv2.waitKey(0)