TCN, Temporal Convolutional Networks
- 时间卷积网络与膨胀卷积:深入理解其原理与应用
- 一、时间卷积网络(TCN)简介
- 二、膨胀卷积的核心概念
- 1. **膨胀卷积(Dilated Convolution)**
- 2. **Kernel(卷积核)**
- 3. **Dilation(膨胀因子)**
- 三、膨胀卷积在TCNs中的应用
- 四、确定卷积核大小(Kernel)
- 1. **实验和经验**
- 2. **任务依赖性**
- 3. **感受野需求**
- 五、确定膨胀因子(Dilation)
- 1. **指数增长策略**
- 2. **最大膨胀因子**
- 3. **层数和膨胀循环**
- 六、综合考虑
时间卷积网络与膨胀卷积:深入理解其原理与应用
在深度学习的世界中,卷积神经网络(CNN)已广泛应用于图像处理和视频分析领域。然而,对于序列数据处理,尤其是在时间序列分析中,传统的卷积神经网络面临一定的局限性。为了解决这些问题,时间卷积网络(TCN, Temporal Convolutional Networks)和其中的膨胀卷积技术应运而生。本文将详细探讨膨胀卷积的概念、其在TCNs中的应用,以及kernel和dilation的具体含义。
一、时间卷积网络(TCN)简介
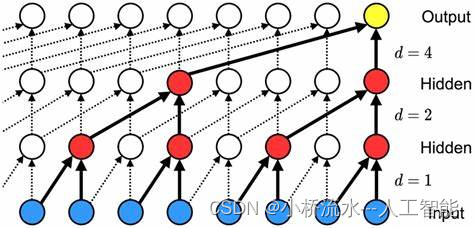
时间卷积网络是一种特别为处理时间序列数据设计的神经网络架构。它利用因果卷积层来保证模型在预测未来信息时只能访问到当前和过去的信息。TCN的关键优势在于它能够处理长序列的输入,同时保持较低的计算复杂性和较高的预测性能。
二、膨胀卷积的核心概念
1. 膨胀卷积(Dilated Convolution)
膨胀卷积,也称为扩张卷积,是一种特殊类型的卷积操作,旨在让卷积核覆盖更广泛的输入区域,而不增加额外的计算负担或参数数量。它通过在标准卷积核的元素之间插入固定数量的空格来实现这一点。
2. Kernel(卷积核)
在膨胀卷积中,kernel指的是执行卷积操作的窗口大小,即在输入数据上滑动以产生输出特征图的矩阵区域。Kernel的大小直接影响卷积层可以捕获的输入数据的局部特征的范围。
3. Dilation(膨胀因子)
Dilation是膨胀卷积中的一个关键参数,定义了卷积核内元素的间隔。例如,当dilation为1时,膨胀卷积就是常规的卷积。随着dilation值的增加,卷积核覆盖的输入数据区域更广,但实际参与运算的元素数量并未增加,因此计算复杂度保持不变。
三、膨胀卷积在TCNs中的应用
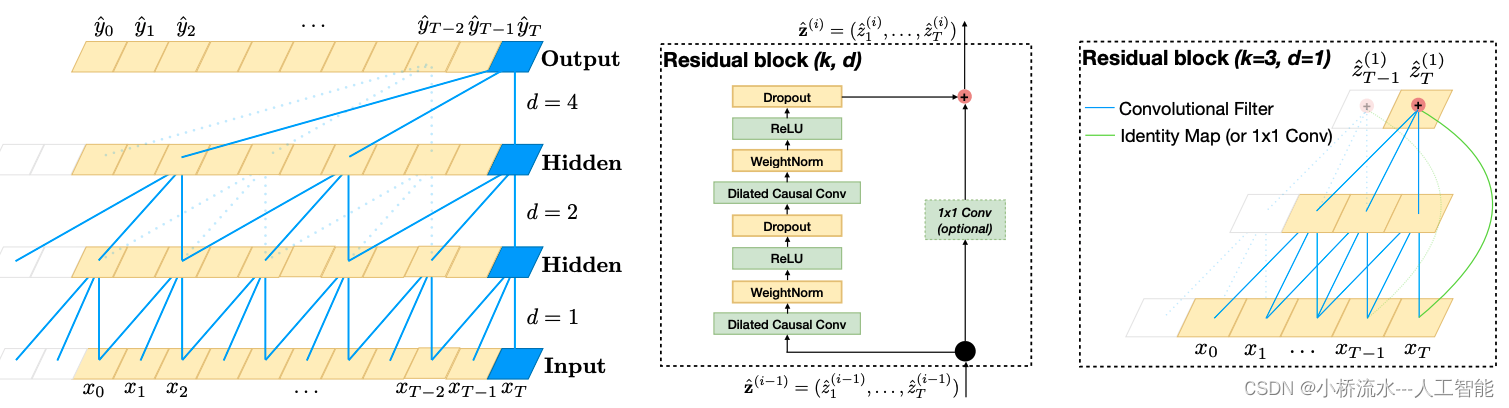
在时间卷积网络中,膨胀卷积使网络能够具有更大的“感受野”(即网络能观察到的输入数据的范围)。通过逐层增加dilation值,TCN能够在不显著增加计算成本的情况下,捕获长期依赖关系。这种结构特别适用于需要分析整个时间序列的场景,如语音信号处理、股票市场预测和各种形式的序列生成任务。
在时间卷积网络(TCN)中,选择合适的 Kernel(卷积核大小)和Dilation(膨胀因子)对于确保模型效能和效率至关重要。这些参数决定了模型的感受野(即模型可以“看到”的输入数据的范围),以及模型可以捕获的时间依赖性的长短。下面将详细介绍如何确定这两个参数,并提供一些实际应用中的策略和考虑因素。
四、确定卷积核大小(Kernel)
卷积核大小是影响模型性能的重要因素之一。选择合适的卷积核大小通常需要平衡模型的性能和计算复杂度:
1. 实验和经验
通常,卷积核的大小选择依赖于具体任务和数据的特性。在实践中,常见的选择是从较小的卷积核开始实验(如3、5或7),通过交叉验证来观察模型在验证集上的性能表现。
2. 任务依赖性
- 对于涉及细粒度特征的任务(如文本处理),较小的卷积核可能更合适。
- 对于需要捕捉较长范围内依赖的任务(如音频处理),较大的卷积核可能更有效,因为它可以在每层捕获更广泛的上下文信息。
3. 感受野需求
卷积核的大小直接影响单层网络的感受野。较大的卷积核可以增加单层的感受野,但也可能增加过拟合的风险和计算成本。
五、确定膨胀因子(Dilation)
膨胀因子的选择关键在于如何有效地增加网络的感受野,同时保持参数数量和计算复杂度的平衡:
1. 指数增长策略
一个常用的方法是指数级增加膨胀因子,例如1, 2, 4, 8, 16等。这种策略可以迅速扩大感受野,允许网络层以对数级复杂度捕捉长距离的信息。
2. 最大膨胀因子
确定一个最大的膨胀因子是有用的,这通常基于输入序列的长度和所需的最大感受野。例如,如果输入序列非常长,较大的膨胀因子可以帮助模型在深层网络中捕捉到起始输入的信息。
3. 层数和膨胀循环
如果模型包含多个卷积层,膨胀因子可以设计成循环使用。例如,在一个有八层的模型中,膨胀因子可以按照1, 2, 4, 8, 1, 2, 4, 8的顺序设置,这样可以在不过度增加计算复杂度的情况下,多次覆盖整个输入序列。
六、综合考虑
在确定这些参数时,最重要的是考虑模型的特定需求和实际应用场景。一般来说,确定这些参数的过程需要多次实验和调整,以找到最佳的性能和效率平衡点。使用像网格搜索这样的超参数优化技术可以系统地探索不同的参数组合,以优化模型性能。
总之,Kernel和Dilation的选择是一个需要根据具体应用进行调整的过程,涉及到对模型结构的深入理解和大量的实验验证。正确的参数设置可以显著提高模型的效果,使其更适应于处理复杂的时间序列数据。