【LeetCode】4，寻找两个正序数组中的中位数

题目地址
B站那个官方解答视频实在看不懂，我就根据他那个代码和自己的理解写一篇文章

1. 基本思路

在只有一个有序数组的时候，中位数把数组分割成两个部分。中位数的定义：中位数，又称中点数，中值。中位数是按顺序排列的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比他大，有一半的数据比他小，如果数据个数为奇数的时候，则排序后的数据最中间的数是中位数，如果数据个数为偶数的时候，则排序后的数据最中间的两个数的均值称为中位数。
根据中位数的定义，我们要分数组长度为奇数和偶数进行讨论：
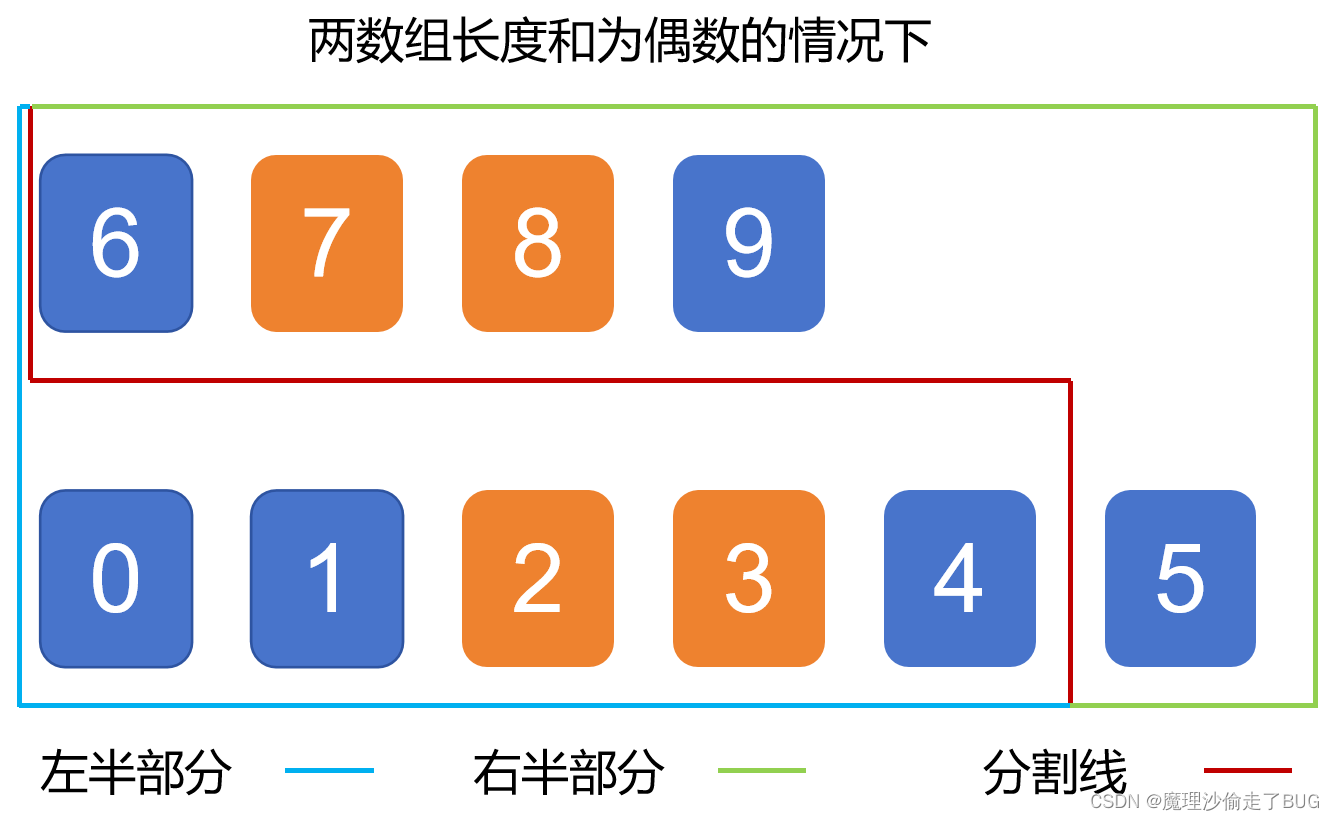
（1）首先，将数组一分为二，数组长度为偶数的时候，中位数有两个，其中一个是左边数组的最大值，另一个是右边数组的最小值。

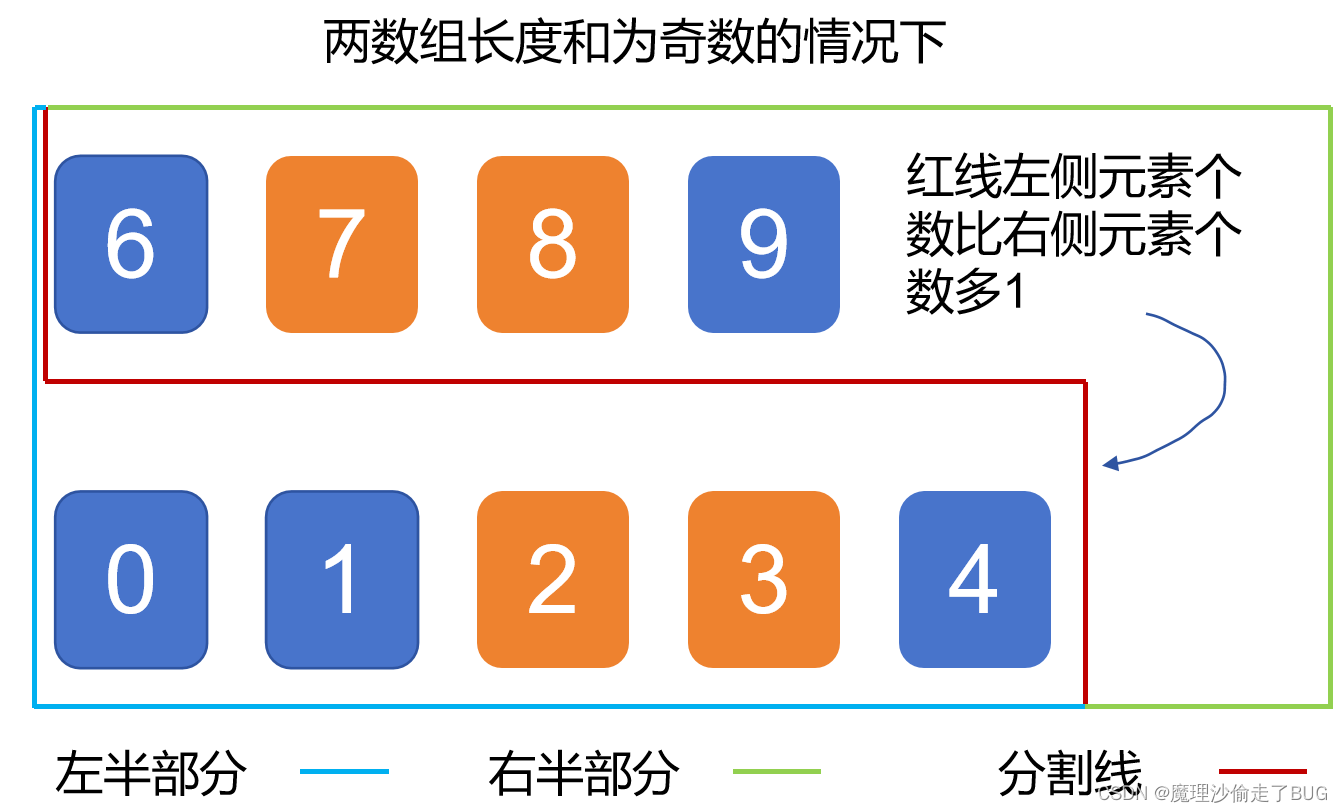
数组长度为奇数的时候，中位数有1个，不妨设中位数分到左边数组。

在两个有序数组的时候，我们仍然可以把两个数组分别按照上面的规则分割为两个部分（注意是将两个数组排成两行然后再对这个整体分割，不是单独分割去分割两个数组中的每一个数组）。
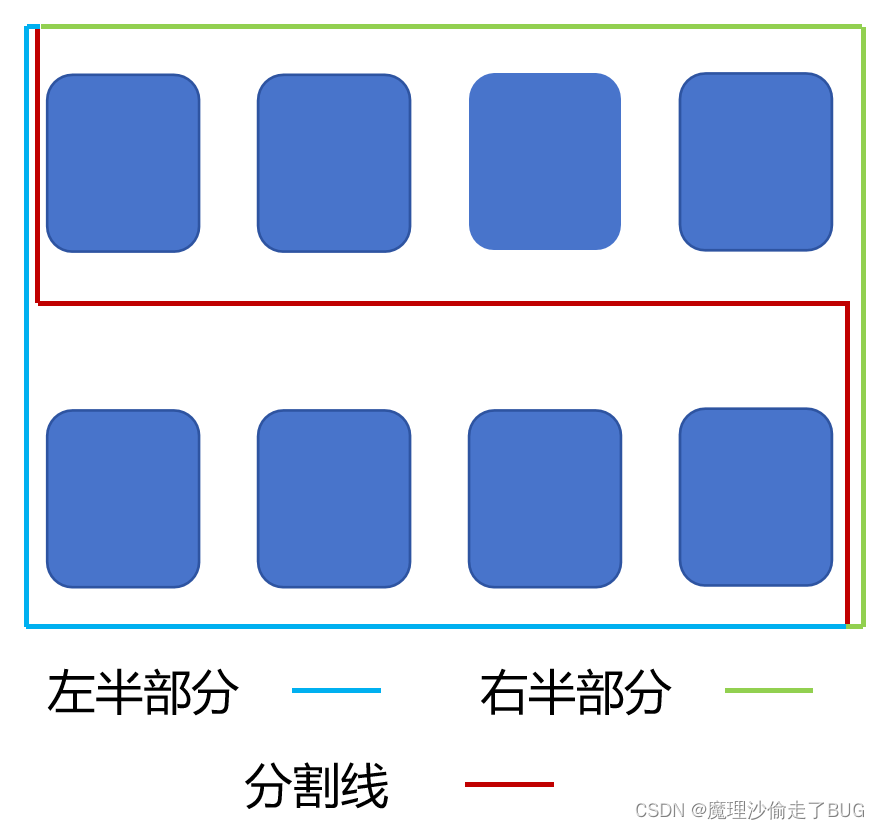
我们使用一条分割线把两个数组分别分割成两部分：
（1）如果两个数组的长度之和为偶数，则让红线左边和右边的元素个数相等；如果两个数组的长度之和为奇数，则让红线左边元素的个数比右边元素的个数多1个；
（2）红线左边的所有元素的值 $\le$ 红线右边的所有元素的值；
那么中位数就一定只与红线两侧的元素有关，确定这条红线的位置使用二分查找。

优化第1个条件：
假设数组1的长度为 $m$ ，数组2的长度为 $n$
当 $m + n$ 为偶数的时候，左侧数组长度为 $\frac{m+n}{2}$
当 $m + n$ 为奇数的时候，由于我们之前假设中位数被分到左边，则左侧数组长度为 $\frac{m+n+1}{2}$ （即向上取整）
由于整数除法是向下取整，则可以将当 $m + n$ 为偶数的时候，左侧数组长度等效为 $\frac{m+n+1}{2}$
因此，左侧数组长度可以合并为 $\frac{m+n+1}{2}$
优化第2个条件：
为了保持红线左边的所有元素的值 $\le$ 红线右边的所有元素的值，由于两个数组都是有序数组，在同一个数组内，分割线一定满足左边的所有元素小于等于右边元素。在不同的数组之间，应该保证交叉小于等于关系成立，如下图：

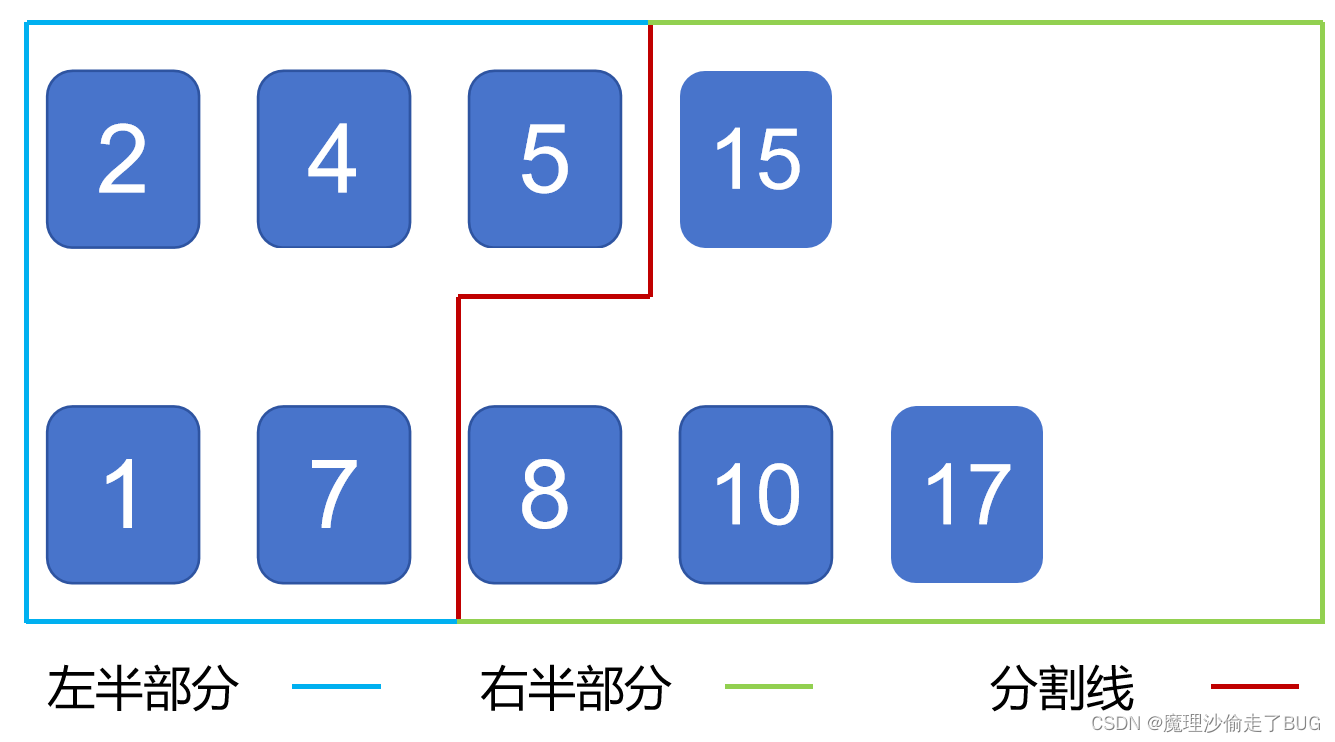
那么只要不符合小于等于关系，我们就需要适当调整分割线的位置。
（1）情况1

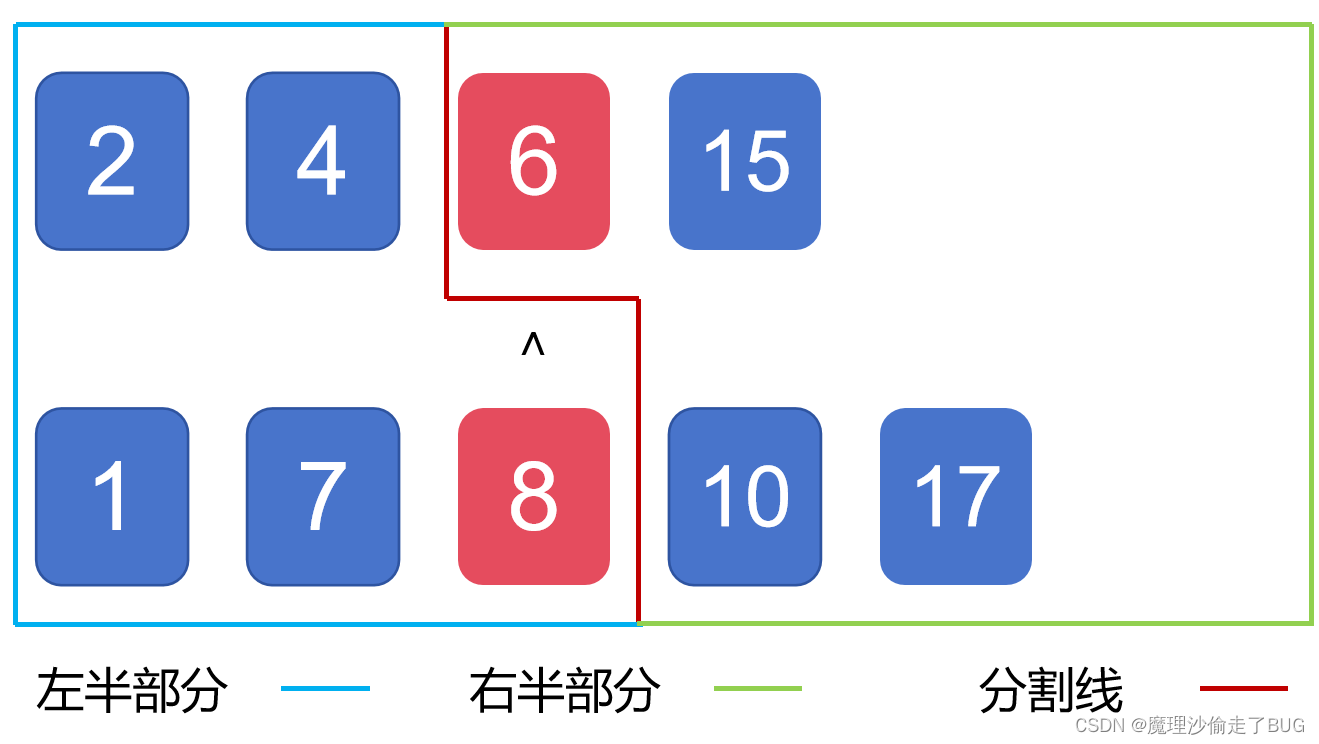
虽然这个是数组之和为奇数，左半部分数组的元素个数比右半部分数组的元素个数多1，但是第二个数组（1, 7, 8, 10, 17)分割线左边位置的最大值8>第一个数组(2, 4, 6, 15)分割线右边位置的最小值6就不符合红线左边的所有元素的值 $\le$ 红线右边的所有元素的值，也就是说中位数右边的数太小了，调整方案：将中位数分割线在数组1的位置右移
（2）情况2：

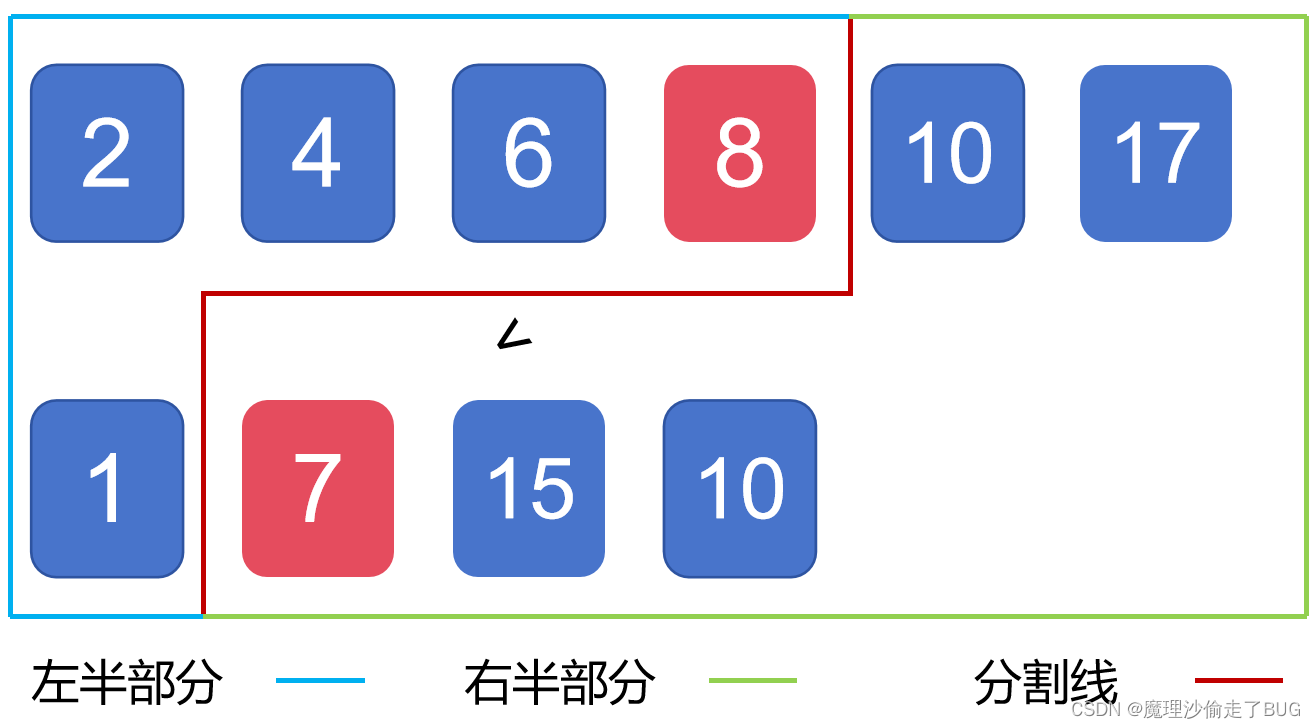
第一个数组（2, 4, 6, 8, 10, 17)分割线左边位置的最大值8>第二个数组(1, 7, 15, 10)分割线右边位置的最小值7就不符合红线左边的所有元素的值 $\le$ 红线右边的所有元素的值，也就是说中位数左边的数太大了，调整方案：将中位数分割线在数组1的位置左移

二分查找算法就是在这样尝试找到恰当的分割线的过程当中，不断地缩小搜索区间的范围，直到最终找到符合条件的分割线的位置，又由于我们需要比较分割线两侧元素的大小关系，在返回数组下标的时候，很有可能就出现下面两类极端的情况：
（1）较短的数组在分割线的右边没有元素和较短的数组在分割线的左边没有元素

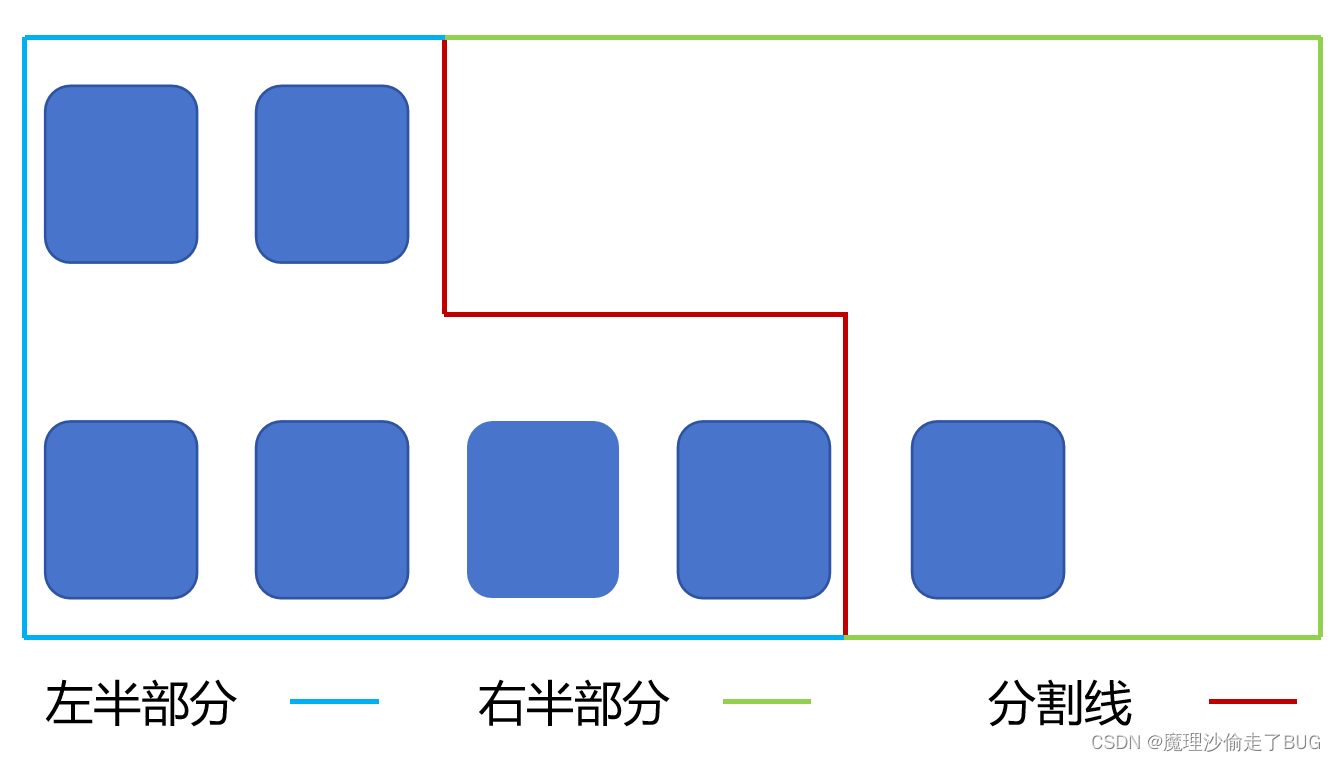
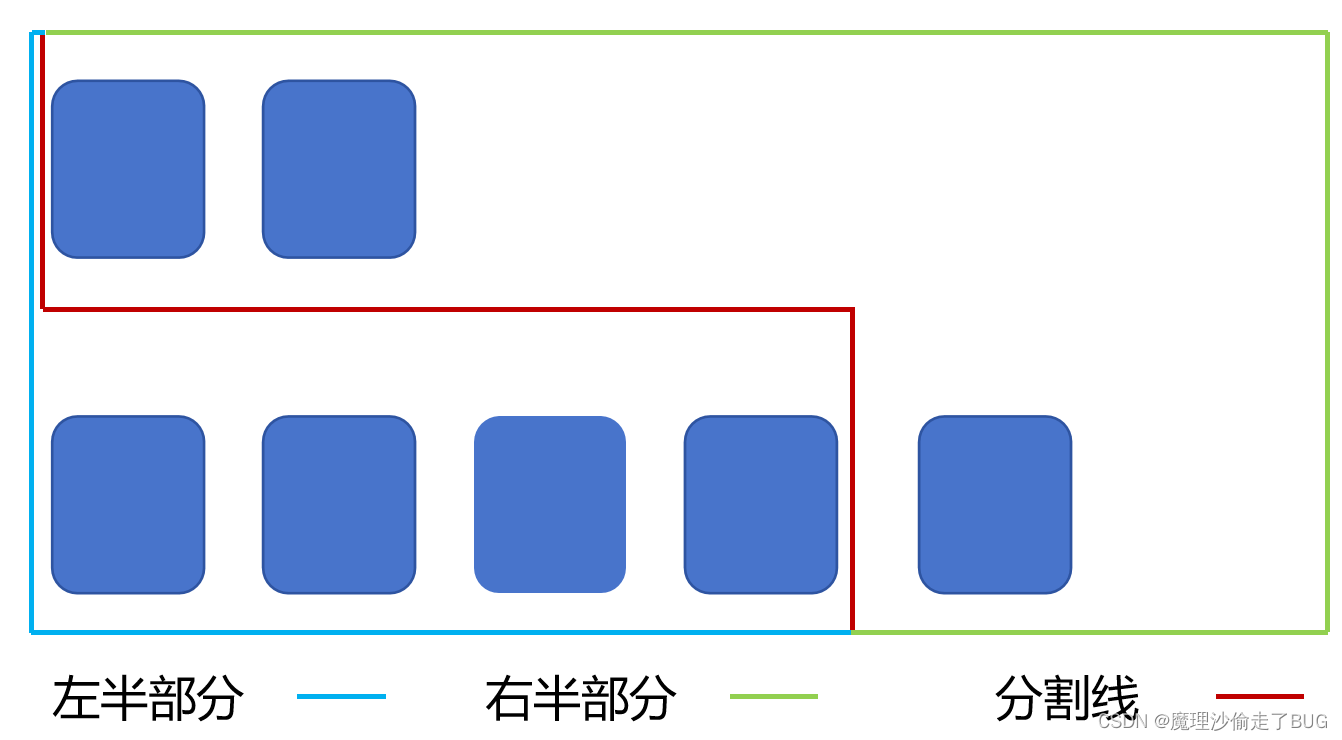
由于我们需要通过访问“中间数分割线”左右两边的元素，因此应该在较短的数组上确定“中间数分割线”的位置。
（3）第二类情况发生在两个数组长度相等的时候
第一种，第一个数组在分割线的右边没有元素，并且第二个数组在分割线的左边没有元素

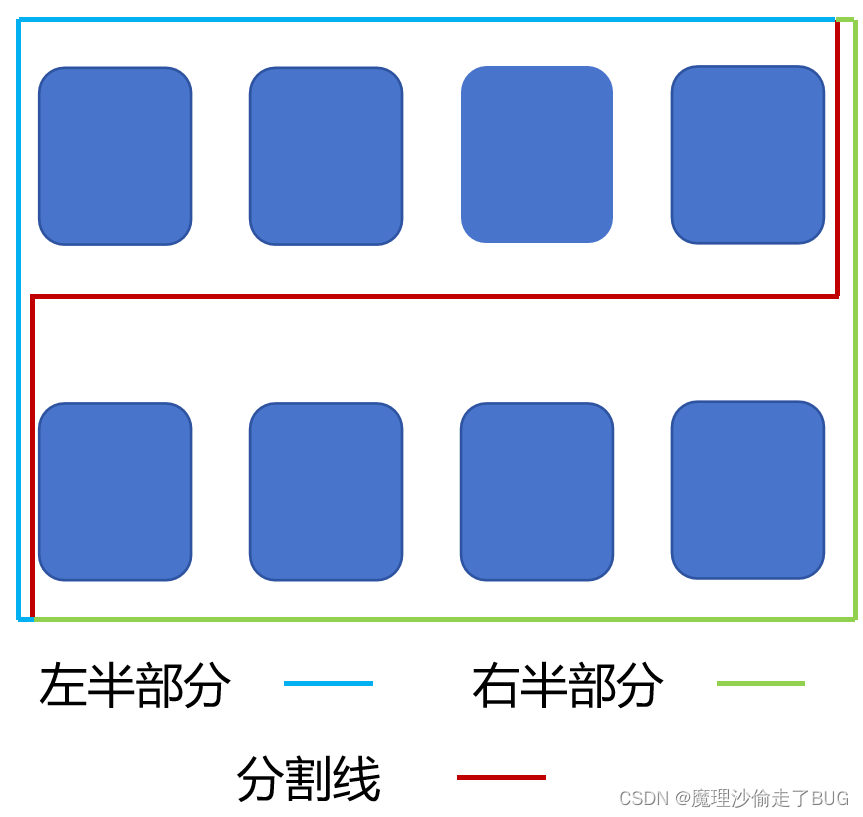
第二章，第二个数组在分割线的左边没有元素，并且第二个数组在分割线的右边没有元素

分割线的定义：
分割线在第一个数组右边的第1个元素的下标为i = 分割线在第一个数组左边的元素个数
分割线在第二个数组右边的第1个元素的下标为j = 分割线在第二个数组左边的元素个数

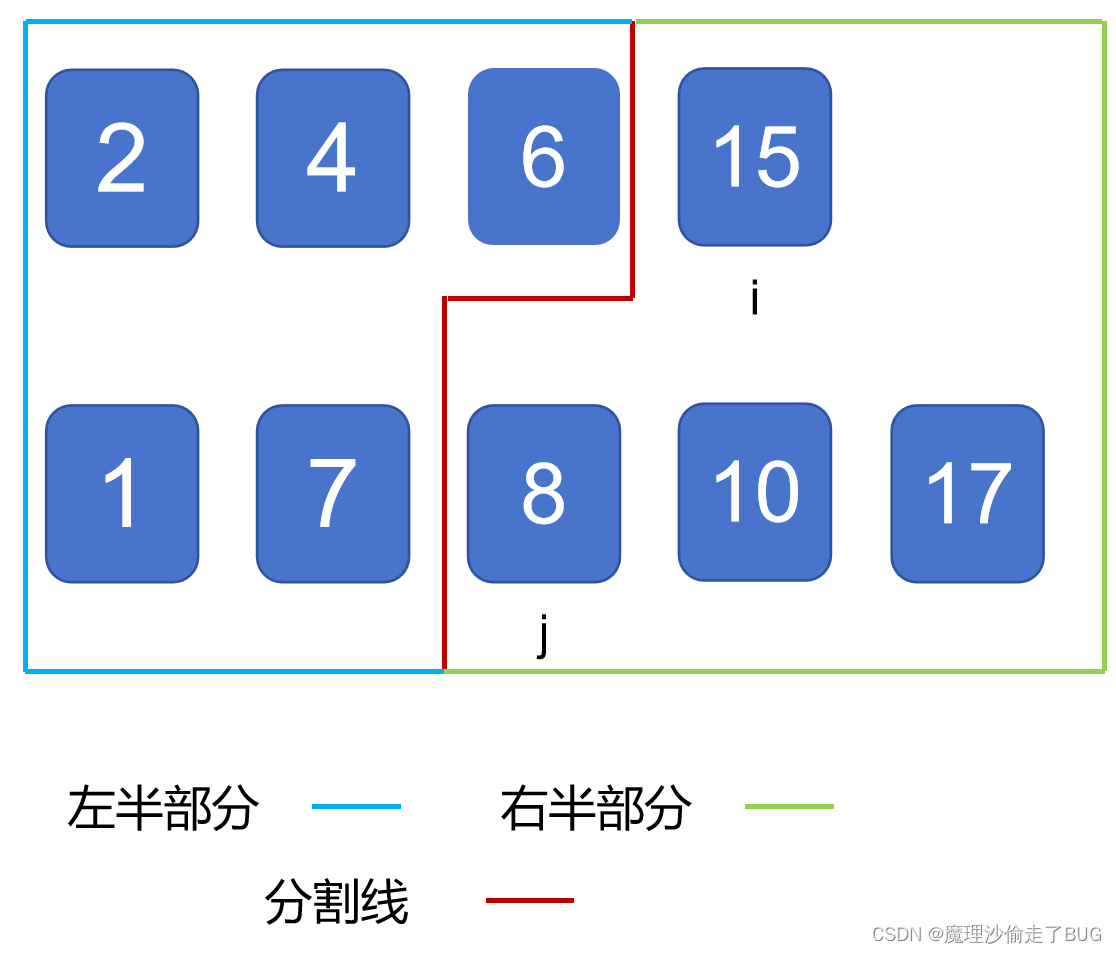
观察到，两数组长度和为奇数的时候，每个数组的分割线左侧的第一个元素的最大值即为中位数，两数组长度和为偶数的时候，每个数组的分割线左侧的第一个元素的最大值和右侧的第一个元素的最小值的均值即为中位数。

2. 代码实现

C语言实现该题，思路全在注释中：

//选出两个整数之间的最小值和最大值
int Min(int a, int b)
{
    if (a > b)
    {
        return b;
    }
    else
    {
        return a;
    }
}
int Max(int a, int b)
{
    if (a < b)
    {
        return b;
    }
    else
    {
        return a;
    }
}
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    //如果有空数组，则直接返回非空数组的中位数
    if(nums1 == NULL || nums1Size == 0)
    {
        //奇数长度返回中间，偶数取中间两个均值
        if(nums2Size % 2 == 0)
        {
            int mid = (nums2Size - 1) >> 1; //返回的是下标中点，不是数量中点
            return (double)((nums2[mid] + nums2[mid + 1]) / 2.0);
        }
        else
        {
            return nums2[nums2Size / 2];
        }
    }
    if(nums2 == NULL || nums2Size == 0)
    {
        //奇数长度返回中间，偶数取中间两个均值
        if(nums1Size % 2 == 0)
        {
            int mid = (nums1Size - 1) >> 1;
            return (double)((nums1[mid] + nums1[mid + 1]) / 2.0);
        }
        else
        {
            return nums1[nums1Size / 2];
        }
    }
    //如果第一个数组的长度大于第二个数组的长度，那就交换以下，让较短的数组成为第一个数组
    if(nums1Size > nums2Size)
    {
        //交换数组指针
        int* temp = nums1;
        nums1 = nums2;
        nums2 = temp;
        //交换数组长度变量
        int tmp = nums1Size;
        nums1Size = nums2Size;
        nums2Size = tmp;
    }
    //数组1和数组2的长度分别用变量m和n表示
    int m = nums1Size;
    int n = nums2Size;
    //分割线左侧元素个数
    int totalLeft = (m + n + 1)>>1; //向右移动1位相当于除2
    //在nums1的区间[0, m]里查找恰当的分割线。
    //分割线在第一个数组左边的最大值nums1[i-1]要小于等于分割线在第二个数组右边的最小值nums2[j]
    //并且，分割线在第二个数组左边的最大值nums2[j-1]要小于等于分割线在第一个数组右边的最小值nums1[i]
    //这个就是我们分析出来的交叉的不等关系
    int left = 0;
    int right = m;
    //以长度最小的数组做循环变量的二分
    while(left < right)
    {
        //分割线在第一个数组的下标
        //+1的原因：
        //比如偶数长度的数组[1, 2, 3, 4]
        //开始的(left + right) / 2为1，其实我们的i应该是分割线右侧，即i为2，我们应该向上取整，向上取整就应该+1后再除2
        //奇数长度因为我们也要将i设置为中位数右侧第一个元素下标的值（对应上面文中的规则）
        int i = (left + right + 1) >> 1;
        //分割线在第二个数组的下标
        //比如两个数组[1, 2]和[3, 4, 5, 6]
        //i=0，则我们没有把第二个数组的开始和结束下标记作left和right
        //只能通过totalLeft间接推出
        //totalLeft=3，totalLeft是两个数组合并后的相对的左侧数组的元素个数
        //totalLeft-i相当于把左侧数组中第一个数组左侧的元素数减掉，只剩下第二个数组左侧的元素数
        //第二个数组左侧元素的个数恰好就是第二个数组的分割线的位置j
        int j = totalLeft - i;
        // 第一个数组中分割线左侧的元素大于第二个数组中分割线右侧的元素
        // 说明分割线在第一个数组上的位置太靠右了，所以分割线位置在i这个位置的左侧（不包括i）
        // 所以下一轮位置，所以下一轮搜索区间是[left, i - 1]
        if(nums1[i-1] > nums2[j])
        {
            right = i - 1;
        }
        //
        else
        // 如果恰好满足条件了，则将第一个数组右侧的元素和第二个数组左侧的元素算作两个新数组继续二分
        {
            left = i;
        }
    }
    //确定二分到最后的数组的分割线
    int i = left;
    int j = totalLeft - i;
    //求出第一个数组的分割线的左侧的最大值和右侧的最小值的变量
    //第二个数组以此类推
    //先初始化为0
    int nums1LeftMax = 0;
    int nums1RightMin = 0;
    int nums2LeftMax = 0;
    int nums2RightMin = 0;
    //如果最后的分割线i为0时，说明第一个数组分割线左侧数组的最大值不存在，则令此时的nums1LeftMax = INT_MIN
    //如果最后的分割线i为m时，说明第一个数组分割线右侧数组的最小值不存在，则令此时的nums1RightMin = INT_MAX
    //同理第二个数组j为0或者n时，以此类推
    if(i == 0)
    {
        nums1LeftMax = INT_MIN;
        nums1RightMin = nums1[i];
    }
    else if(i == m)
    {
        nums1LeftMax = nums1[i-1];
        nums1RightMin = INT_MAX;
    }
    else
    {
        nums1LeftMax = nums1[i-1];
        nums1RightMin = nums1[i];
    }
    if(j == 0)
    {
        nums2LeftMax = INT_MIN;
        nums2RightMin = nums2[j];
    }
    else if(j == n)
    {
        nums2LeftMax = nums2[j-1];
        nums2RightMin = INT_MAX;
    }
    else
    {
        nums2LeftMax = nums2[j-1];
        nums2RightMin = nums2[j];
    }
    //如果是奇数，返回的是分割线左侧的两个数组对应的元素的最大值
    //即分割线左侧要找到的是最大值
    //如果是偶数，返回的是分割线左侧的两个数组对应的元素的最大值和右侧的最小值的均值
    if((n+m)%2 == 1)
    {
        return Max(nums1LeftMax, nums2LeftMax);
    }
    else
    {
        return (double)((Max(nums1LeftMax, nums2LeftMax) + Min(nums1RightMin, nums2RightMin)) / 2.0);
    }
}