数组
数组(Array) 是一种很常见的数据结构。它由相同类型的元素(element)组成,并且是使用一块连续的内存来存储。
我们直接可以利用元素的索引(index)可以计算出该元素对应的存储地址。
数组的特点是:提供随机访问 并且容量有限。
链表
链表(LinkedList) 虽然是一种线性表,但是并不会按线性的顺序存储数据,使用的不是连续的内存空间来存储数据。
链表的插入和删除操作的复杂度为 O(1) ,只需要知道目标位置元素的上一个元素即可。但是,在查找一个节点或者访问特定位置的节点的时候复杂度为 O(n) 。
使用链表结构可以克服数组需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但链表不会节省空间,相比于数组会占用更多的空间,因为链表中每个节点存放的还有指向其他节点的指针。除此之外,链表不具有数组随机读取的优点。
链表分类
- 单链表
单链表 单向链表只有一个方向,结点只有一个后继指针 next 指向后面的节点。因此,链表这种数据结构通常在物理内存上是不连续的。我们习惯性地把第一个结点叫作头结点,链表通常有一个不保存任何值的 head 节点(头结点),通过头结点我们可以遍历整个链表。尾结点通常指向 null。
- 双向链表
双向链表 包含两个指针,一个 prev 指向前一个节点,一个 next 指向后一个节点。

- 循环链表
循环链表 其实是一种特殊的单链表,和单链表不同的是循环链表的尾结点不是指向 null,而是指向链表的头结点。
- 双向循环链表
双向循环链表 最后一个节点的 next 指向 head,而 head 的 prev 指向最后一个节点,构成一个环。

数组与链表
- 数组支持随机访问,而链表不支持。
- 数组使用的是连续内存空间对 CPU 的缓存机制友好,链表则相反。
- 数组的大小固定,而链表则天然支持动态扩容。如果声明的数组过小,需要另外申请一个更大的内存空间存放数组元素,然后将原数组拷贝进去,这个操作是比较耗时的!
栈
栈 (Stack) 只允许在有序的线性数据集合的一端(称为栈顶 top)进行加入数据(push)和移除数据(pop)。因而按照 后进先出(LIFO, Last In First Out) 的原理运作。在栈中,push 和 pop 的操作都发生在栈顶。
队列
队列(Queue) 是 先进先出 (FIFO,First In, First Out) 的线性表。在具体应用中通常用链表或者数组来实现,用数组实现的队列叫作 顺序队列 ,用链表实现的队列叫作 链式队列 。队列只允许在后端(rear)进行插入操作也就是入队 enqueue,在前端(front)进行删除操作也就是出队 dequeue)
队列的操作方式和堆栈类似,唯一的区别在于队列只允许新数据在后端进行添加。
图
简单来说,图就是由顶点的有穷非空集合和顶点之间的边组成的集合。通常表示为:G(V,E),其中,G 表示一个图,V 表示顶点的集合,E 表示边的集合。
无向图与有向图
边表示的是顶点之间的关系,有的关系是双向的,比如同学关系,A 是 B 的同学,那么 B 也肯定是 A 的同学,那么在表示 A 和 B 的关系时,就不用关注方向,用不带箭头的边表示,这样的图就是无向图。
有的关系是有方向的,比如父子关系,师生关系,微博的关注关系,A 是 B 的爸爸,但 B 肯定不是 A 的爸爸,A 关注 B,B 不一定关注 A。在这种情况下,我们就用带箭头的边表示二者的关系,这样的图就是有向图。
无权图与带权图
对于一个关系,如果我们只关心关系的有无,而不关心关系有多强,那么就可以用无权图表示二者的关系。
对于一个关系,如果我们既关心关系的有无,也关心关系的强度,比如描述地图上两个城市的关系,需要用到距离,那么就用带权图来表示,带权图中的每一条边一个数值表示权值,代表关系的强度。
图的存储
邻接矩阵将图用二维矩阵存储,是一种较为直观的表示方式。
邻接矩阵存储的方式优点是简单直接(直接使用一个二维数组即可),并且,在获取两个定点之间的关系的时候也非常高效(直接获取指定位置的数组元素的值即可)。但是,这种存储方式的缺点也比较明显,那就是比较浪费空间。
针对邻接矩阵比较浪费内存空间的问题,诞生了图的另外一种存储方法—邻接表 。
邻接链表使用一个链表来存储某个顶点的所有后继相邻顶点。对于图中每个顶点 Vi,把所有邻接于 Vi 的顶点 Vj 链成一个单链表,这个单链表称为顶点 Vi 的 邻接表
图的搜索
广度优先搜索就像水面上的波纹一样一层一层向外扩展。
广度优先搜索的具体实现方式用到了之前所学过的线性数据结构——队列。
深度优先搜索就是“一条路走到黑”,从源顶点开始,一直走到没有后继节点,才回溯到上一顶点,然后继续“一条路走到黑”。
深度优先搜索的具体实现用到了另一种线性数据结构——栈 。
堆
堆中的每一个节点值都大于等于(或小于等于)子树中所有节点的值。或者说,任意一个节点的值都大于等于(或小于等于)所有子节点的值。
- 堆不一定是完全二叉树,只是为了方便存储和索引,我们通常用完全二叉树的形式来表示堆,事实上,广为人知的斐波那契堆和二项堆就不是完全二叉树,它们甚至都不是二叉树。
- (二叉)堆是一个数组,它可以被看成是一个 近似的完全二叉树。
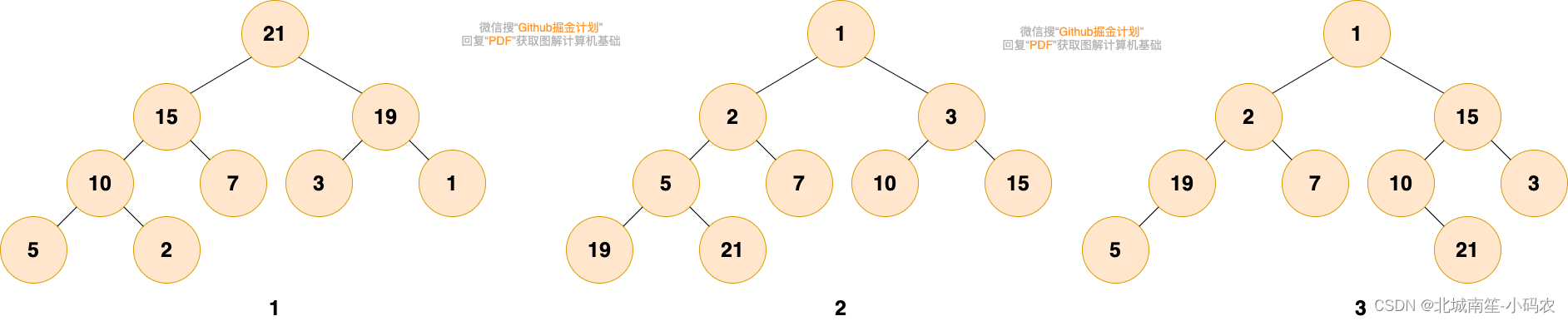
第 1 个和第 2 个是堆。第 1 个是最大堆,每个节点都比子树中所有节点大。第 2 个是最小堆,每个节点都比子树中所有节点小。
第 3 个不是,第三个中,根结点 1 比 2 和 15 小,而 15 却比 3 大,19 比 5 大,不满足堆的性质。
相对于有序数组而言,堆的主要优势在于插入和删除数据效率较高。 因为堆是基于完全二叉树实现的,所以在插入和删除数据时,只需要在二叉树中上下移动节点,时间复杂度为 O(log(n)),相比有序数组的 O(n),效率更高。
不过,需要注意的是:Heap 初始化的时间复杂度为 O(n),而非O(nlogn)。
树
树就是一种类似现实生活中的树的数据结构(倒置的树)。任何一颗非空树只有一个根节点。
一棵树具有以下特点:
- 一棵树中的任意两个结点有且仅有唯一的一条路径连通。
- 一棵树如果有 n 个结点,那么它一定恰好有 n-1 条边。
- 一棵树不包含回路。

- 节点:树中的每个元素都可以统称为节点。
- 根节点:顶层节点或者说没有父节点的节点。上图中 A 节点就是根节点。
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。上图中的 B 节点是 D 节点、E 节点的父节点。
- 子节点:一个节点含有的子树的根节点称为该节点的子节点。上图中 D 节点、E 节点是 B 节点的子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。上图中 D 节点、E 节点的共同父节点是 B 节点,故 D 和 E 为兄弟节点。
- 叶子节点:没有子节点的节点。上图中的 D、F、H、I 都是叶子节点。
- 节点的高度:该节点到叶子节点的最长路径所包含的边数。
- 节点的深度:根节点到该节点的路径所包含的边数
- 节点的层数:节点的深度+1。
- 树的高度:根节点的高度。
二叉树
二叉树(Binary tree)是每个节点最多只有两个分支(即不存在分支度大于 2 的节点)的树结构。
二叉树 的分支通常被称作“左子树”或“右子树”。并且,二叉树 的分支具有左右次序,不能随意颠倒。
完全二叉树
除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则这个二叉树就是 完全二叉树 。

完全二叉树有一个很好的性质:父结点和子节点的序号有着对应关系。
平衡二叉树
平衡二叉树 是一棵二叉排序树,且具有以下性质:
- 可以是一棵空树
- 如果不是空树,它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
平衡二叉树的常用实现方法有 红黑树、AVL 树、替罪羊树、加权平衡树、伸展树 等。

二叉树的存储
二叉树的存储主要分为 链式存储 和 顺序存储 两种。
链式存储和链表类似,二叉树的链式存储依靠指针将各个节点串联起来,不需要连续的存储空间。
每个节点包括三个属性:
- 数据 data。data 不一定是单一的数据,根据不同情况,可以是多个具有不同类型的数据。
- 左节点指针 left
- 右节点指针 right。
可是 JAVA 没有指针啊!那就直接引用对象呗!!!
顺序存储就是利用数组进行存储,数组中的每一个位置仅存储节点的 data,不存储左右子节点的指针,子节点的索引通过数组下标完成。根结点的序号为 1,对于每个节点 Node,假设它存储在数组中下标为 i 的位置,那么它的左子节点就存储在 2i 的位置,它的右子节点存储在下标为 2i+1 的位置。

二叉树的遍历
二叉树的先序遍历,就是先输出根结点,再遍历左子树,最后遍历右子树,遍历左子树和右子树的时候,同样遵循先序遍历的规则,也就是说,我们可以递归实现先序遍历。

二叉树的中序遍历,就是先递归中序遍历左子树,再输出根结点的值,再递归中序遍历右子树,大家可以想象成一巴掌把树压扁,父结点被拍到了左子节点和右子节点的中间。
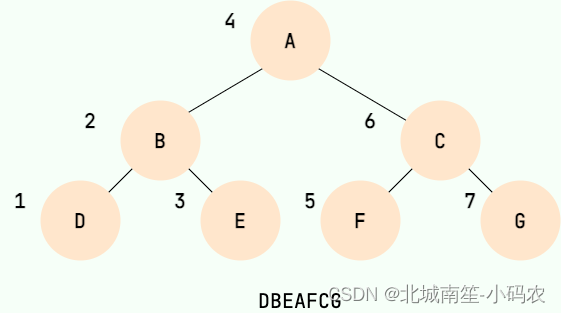
二叉树的后序遍历,就是先递归后序遍历左子树,再递归后序遍历右子树,最后输出根结点的值
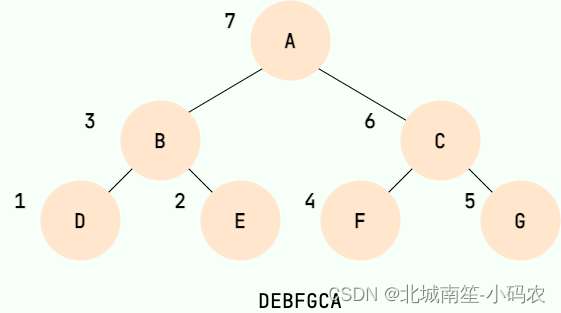
布隆过滤器
布隆过滤器布隆过滤器一个名叫 Bloom 的人提出了一种来检索元素是否在给定大集合中的数据结构,这种数据结构是高效且性能很好的,但缺点是具有一定的错误识别率和删除难度。并且,理论情况下,添加到集合中的元素越多,误报的可能性就越大。
当一个元素加入布隆过滤器中的时候,会进行如下操作:
- 使用布隆过滤器中的哈希函数对元素值进行计算,得到哈希值(有几个哈希函数得到几个哈希值)。
- 根据得到的哈希值,在位数组中把对应下标的值置为 1。
原理:
当一个元素加入布隆过滤器中的时候,会进行如下操作:
-
当一个元素加入布隆过滤器中的时候,会进行如下操作:
- 使用布隆过滤器中的哈希函数对元素值进行计算,得到哈希值(有几个哈希函数得到几个哈希值)。
- 根据得到的哈希值,在位数组中把对应下标的值置为 1。
当我们需要判断一个元素是否存在于布隆过滤器的时候,会进行如下操作:
- 对给定元素再次进行相同的哈希计算;
- 得到值之后判断位数组中的每个元素是否都为 1,如果值都为 1,那么说明这个值在布隆过滤器中,如果存在一个值不为 1,说明该元素不在布隆过滤器中。
综上,我们可以得出:布隆过滤器说某个元素存在,小概率会误判。布隆过滤器说某个元素不在,那么这个元素一定不在!