笔记98：按列压缩矩阵 csc_matrix 的 “含义”

news2025/9/18 22:49:52

1. 如何按列压缩矩阵：

注：按列压缩（Compressed Sparse Column -- CSC），是一种使用三个特征数组就可以表示整个矩阵的方法；

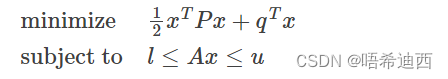
$x$ ：状态量
$P$ ：矩阵
$q$ ：向量
$A$ ：矩阵
$l$ ：向量（x 的最小边界取值限制）
$u$ ：向量（x 的最大边界取值限制）

解释：一般我们在求解二次规划问题的时候，需要将矩阵 P 和 A 传入求解器；但如果我们通过一个个指定矩阵 P 和 A 的每个元素的方式定义矩阵，这样的代码可太脑瘫了；因此我们可以使用按列压缩的方式来表示一个矩阵，这样我们只需要3个特征数组，就可以知道整个矩阵到底是什么样的；需要完整的矩阵 A 和 P 时，将这3个特征数组传入函数 csc_matrix() 就可以了；

如何使用3个特征数组表示一个矩阵：

矩阵： $A=\begin{bmatrix} 1 & 0 &4 \\ 0& 0 &5 \\ 2& 3 &6 \end{bmatrix}$

定义特征数组：

A_data：从左到右按列遍历矩阵 A，记录每一列中每一个非零元素的值
- A_data = [ 1 , 2 , 3 , 4 , 5 , 6 ]
A_indices：从左到右按列遍历矩阵 A，记录每一列上的非零数字的行索引值
- A_indices = [ 0 , 2 , 2 , 0 , 1 , 2 ]
A_indptr：从左到右按列遍历矩阵 A，截止到当前列（不含当前列）时已遍历到的非零元素的个数
- A_indptr = [ 0 , 2 , 3 , 6 ]
- 解释：在数组 A_indptr 的索引为0处，代表当前列为第0列，不含当前列已遍历到的非零元素数量为0；
- 解释：数组 A_indptr 的索引为3处，表示当前列为第3列，代表矩阵 A 的所有列（0~2）都已遍历，非零元素元素个数为6；

注1：通过这三个特征数组就可以得到矩阵 A 原本的模样；将矩阵 A 按列压缩，意思就是得到矩阵 A 的这三个特征数组；
注2：除了按列压缩，还有按行压缩等等各种压缩方法，基本原理一致，在此不再赘述；

2. 如何通过三个特征数组恢复矩阵

有特征数组：

A_data = [ 1 , 2 , 3 , 4 , 5 , 6 ]
A_indices = [ 0 , 2 , 2 , 0 , 1 , 2 ]
A_indptr = [ 0 , 2 , 3 , 6 ]

通过数组 A_indptr = [ 0 , 2 , 3 , 6 ] 可知：

矩阵 A 有3列
第零列 2 个非零元素；第一列 3-2=1 个非零元素；第二列 6-3=3 个非零元素；
可以将 A_indices = [ 0 , 2 | 2 | 0 , 1 , 2 ] 分割为三段，一段代表一列；

通过数组 A_indices = [ 0 , 2 | 2 | 0 , 1 , 2 ] 可知，非零元素位置为：

第0列：(0 , 0) (2 , 0)
第1列：(2 , 1)
第2列：(0 , 2) (1 , 2) (2 , 2)

通过数组 A_data = [ 1 , 2 , 3 , 4 , 5 , 6 ] 给这些位置赋值即可得到矩阵 A；

3. 关于函数 csc_matrix

函数作用：通过传入的三个数组，恢复稀疏矩阵 A 原有的样子；

注1：这个函数是我们自己定义的；这个函数是没有C++版本的，只有Python版本，但是我们可以借助C++的 Eigen 库自己定义这个函数；

注2：我在使用 MPC 控制器控制车辆的运动时，建立了一个二次规划模型，需要使用 OSQP 库进行求解；

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])

参考文章：