图像增强

$$图像增强\{\begin{array}{l}处理方法\{\begin{array}{l}空间域方法\{\begin{array}{l}点处理(变换)\\ \\ 模板处理(滤波)\end{array}\\ 频域方法\end{array}\\ \\ 处理策略\{\begin{array}{l}全局处理\\ 局部处理\end{array}\\ \\ 处理对象\{\begin{array}{l}灰度图像\\ 彩色图像\end{array}\end{array}$$

图像增强：是一类基本的图像处理技术，其目的是对图像进行加工，以得到对视觉解释来说视觉效果“更好”、或对机器感知效果来说“更有用”的图像。

直方图

直方图定义1：一个灰度级在范围$[0,L-1]$的数字图像的直方图是一个离散函数 $h(r_k)=n_k$, $n_k$是图像中灰度级为 $r_k$ 的像素个数， $r_k$ 是第 $k$ 个灰度级， $k=0,1,2,...,L-1$
由于 $r_k$ 的增量是1， 直方图可表示为： $p(k)=n_k$即，图像中不同灰度级像素出现的次数。

直方图定义2：一个灰度级在范围$[0,L-1]$ 的数字图像的直方图是一个离散函数 $p(r_k)=\frac{n_k}{n}$, $n$是图像的像素总数 $n_k$ 是图像中灰度级为 $r_k$ 的像素个数 $r_k$ 是第$k$个灰度级， $k=0,1,\mathrm{2...}，L-1$

而对于定义2，

• 它使得函数正则化到 $[0,1]$ 区间，成为实数函数
• 函数值的范围与像素的总数无关
• 给出灰度级 $r_k$ 在图像中出现的概率密度统计

直方图均衡化
基本思想：所谓直方图均衡化，就是吧一幅图像变化成具有均匀分布的概率密度函数的新图像过程。

如果一幅图像的像素占有很多的灰度级而且分布均匀，那么这样的图像往往有高对比度和多变的灰度色调。直方图均衡化处理的“中心思想”就是将原始图像灰度直方图从比较集中的某个灰度区间变成在全部灰度区间均匀分布，从而实现图像增强。

直方图均衡化是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。

离散情况下的直方图均衡化算法：

1. 列出原始图像的灰度级 $r_j$, $j=0,1,...,L-1$
2. 统计各灰度级的像素数目 $n_j$, $j=0,1,...,L-1$
3. 计算原始图像直方图各灰度级的频率
   $$p_R(r_j)=\frac{n_j}{n},j=0,1,...,L-1$$
4. 计算累计分布函数（求前缀和数组）
   $$S_k=\sum _{j=0}^k{p}_R(r_j),j=0,1,...,L-1$$
5. 把新的灰度级按就近原则转化到原灰度级(将前缀和数组成像素个数并四舍五入)
   $$g_k=INT[(L-1)\times s_k+0.5],INT:取整\Rightarrow 四舍五入$$
6. 用原图像 $r_k$ 和 $g_k$ 的映射关系，修改原图像灰度级，获得输出图像，其直方图为近似均匀分布

例：

直方图均衡化的缺点：

1. 变换后图像的灰度级减少，某些细节消失
2. 某些图像，如直方图有高峰，经处理后对比度不自然的过分增强

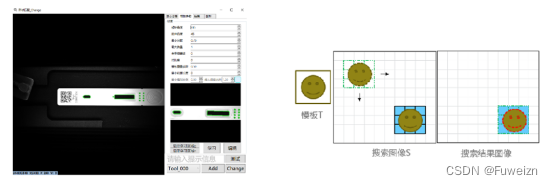
直方图匹配

生成具有指定直方图的已处理图像

局部增强

方法：

1. 定义一个邻域并将其中心从一个像素移动到另一个像素
2. 在每个位置，计算邻域中点的直方图
3. 获得直方图均衡或直方图规范变化函数
4. 映射以邻域为中心的像素的强度移动到下一个为止并重复改过程

空间滤波器

定义：使用空间模板进行的空间处理，被称为空间滤波。模板本身被称为空间滤波器，模板叫窗口、掩模或核。

二维模板通常是一幅具有规则形状的图像，每个像素点具有一定灰度值，模板的尺寸一般远远小于图像的尺寸。

平滑空间滤波器
作用：模糊处理：去除图像中一些不重要的细节，减小噪声
分类：

1. 线性滤波器：均值滤波器
   包含在滤波器邻域内像素的平均值，也称为均值滤波器
   作用：

   • 减小图像灰度的“尖锐”变化，减小噪声
   • 由于图像边缘是由图像灰度尖锐变化引起的，所以也存在边缘模糊的问题

   结论：对相同类型的平滑滤波器，滤波器尺寸越大，细节模糊效应也越强

答：具有相同的直方图，滤波后的直方图不相同

2. 非线性滤波器：
   统计排序滤波器
   • 最大值滤波器：用像素邻域内的最大值代替该像素，主要用途为寻找最亮点
   • 中值滤波器：用像素邻域内的中间值代替该像素，主要用途为去除噪声
   • 最小值滤波器：用像素邻域内的最小是代替该像素，主要用途为寻找最暗点

锐化滤波器
主要用途：

• 突出图像中的细节，增强被模糊了的细节
• 印刷中的细微层次强调，弥补扫描对图像的钝化
• 超声探测成像，分辨率低，边缘模糊，通过锐化来改善
• 图像识别中，分割前的边缘提取
• 锐化处理恢复过渡钝化、曝光不足的图像
• 尖锐武器的目标识别、定位

锐化滤波器的分类：
二阶微分滤波器：拉布拉斯算子
一阶微分滤波器：梯度算子

拉布拉斯锐化算子模板：

梯度算子：

• Sobel锐化算子
  
  

• Prewitt算子
  

• Isotropic Sobel算子
  

空间滤波器小结

• 平滑滤波器：系数都为正，一般系数之和等于1
• 锐化滤波器：系数有正有负，若没有提升，系数之和等于0；否则，系数之和大于0

Q&A:

• 图像锐化与图像平滑的区别与联系？
  • 图像锐化是增强图像中的细节，使边缘和细节更加清晰，适用于图像细节的增强，图像平滑是减少图像中的噪声和细小不规则，使图像更加平滑，图像中的噪声和小细节被抑制，图像显得更柔和
  • 联系：
    频率域：两者都涉及频率域操作。锐化增强高频成分，平滑抑制高频成分
    滤波器：都使用滤波器，锐化用高通滤波器，平滑用低通滤波器
    图像质量：在实际应用中，常常先平滑后锐化，既能去除噪声又能增强细节
• 平滑滤波器和锐化滤波器反复对一幅图像进行处理的结果？
  • 平滑滤波反复对一幅图像进行处理，图像会越来越模糊，最终图像将具有统一的灰度值。
  • 锐化滤波器反复应用虽然能增强边缘和细节，但也会导致噪声放大、伪影出现和细节丢失
• 用系数之和为0的滤波器对图像滤波，滤波后的图像有什么特点？
  • 滤波后图像的平均值为0，导致图像的值有的为正，有的为负，图像的细节部分得到增强，同时放大了噪声。在显示滤波图像时，必须把它转为0到255区间内。