文章目录
- 1. 图灵机与三种基本结构
- 1. 顺序结构
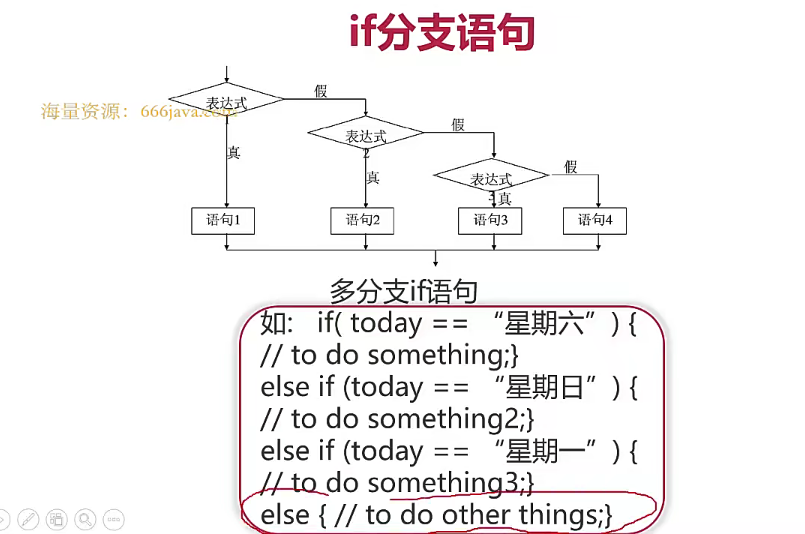
- 2. 分支结构
- 自定义结构-枚举
- 结构体与联合体
- 结构体数据对齐问题
- 3. 循环结构
- 三种循环结构
- 反汇编查看三种结构效率
- 实例:输出所有形如aabb的四位数的完全平方数
- 方案1: 构造aabb数,再判断
- 方案2:反向操作:先算出平方和,再判断是否为aabb结构
- 2. 函数
- 1. 总览
- 2. 函数组成
- 3. 指向函数的指针与返回指针的函数
- 4. 命名空间
- 5. 函数体调用过程
- 6. 内联函数
- VS设置
- 汇编过程
- 3. 递归
- 1. 递归与数学归纳法
- 基本法则
- 递归的缺陷
- 递归的优化
- 循环迭代
- 尾递归
- 动态规划
慕课网c++课程
1. 图灵机与三种基本结构
1. 顺序结构
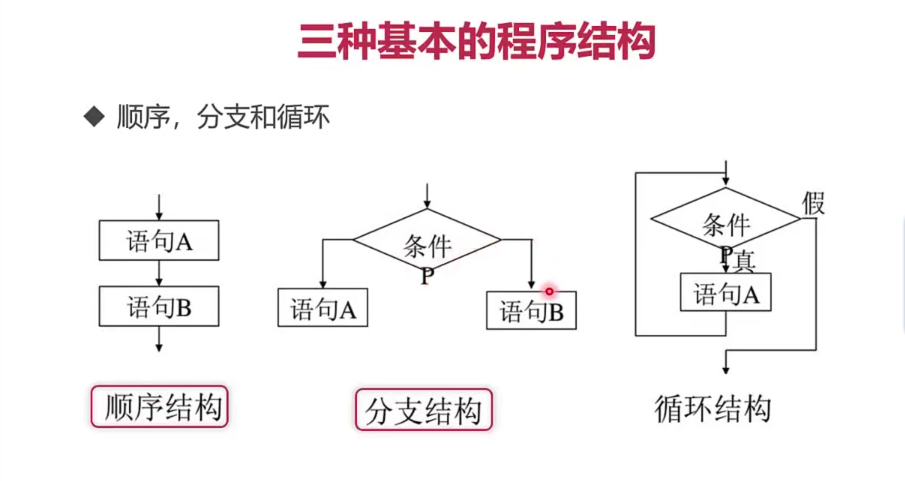
2. 分支结构



自定义结构-枚举

- 代码示例
// demo6-2.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int main()
{
enum wT{Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}; // 声明wT类型
wT weekday;
weekday = Monday;
weekday = Tuesday;
//weekday = 1; // 不能直接给int值,只能赋值成wT定义好的类型值
cout << weekday << endl; // 1
//Monday = 0; // 类型值不能做左值
int a = Wednesday;
cout << a << endl; // 2
return 0;
}

结构体与联合体
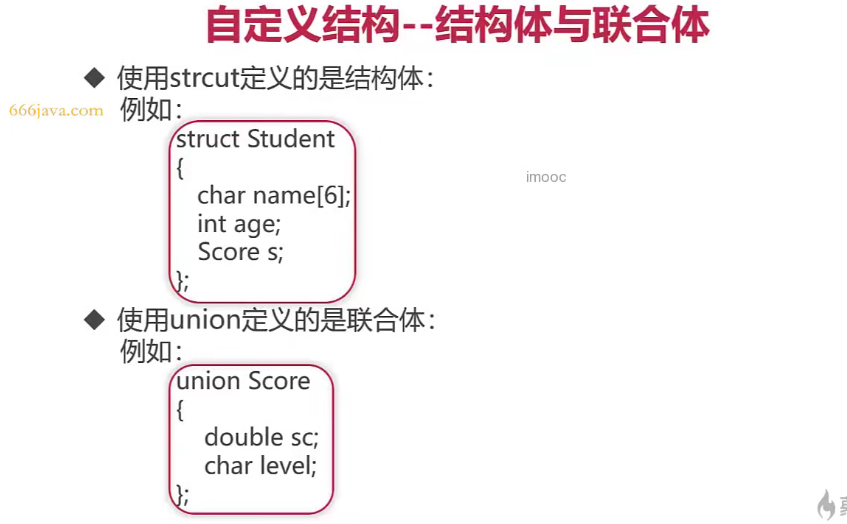
- 示例
#include <string.h>
#include <iostream>
using namespace std;
int main()
{
union Score
{
double ds;
char level;
};
struct Student
{
char name[6];
int age;
Score s;
};
cout << sizeof(Score) << endl; // 8,取最大元素的字节作为联合体空间
...
}
结构体数据对齐问题
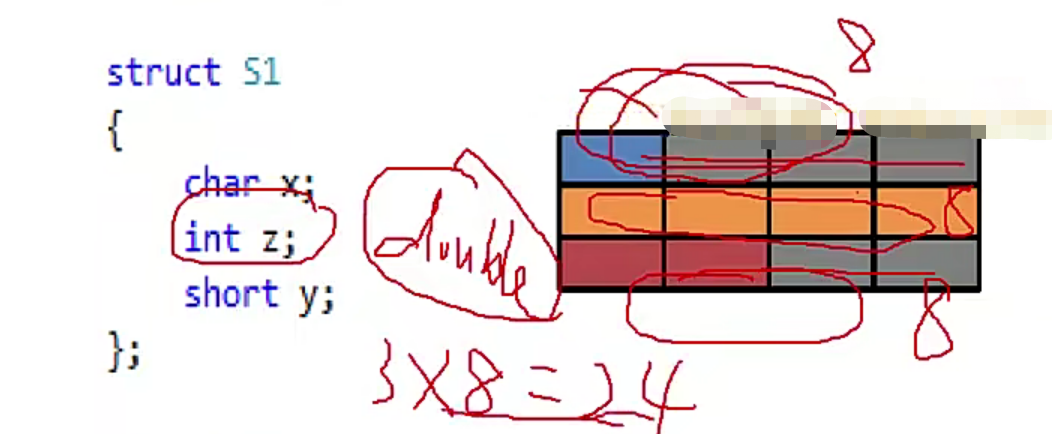
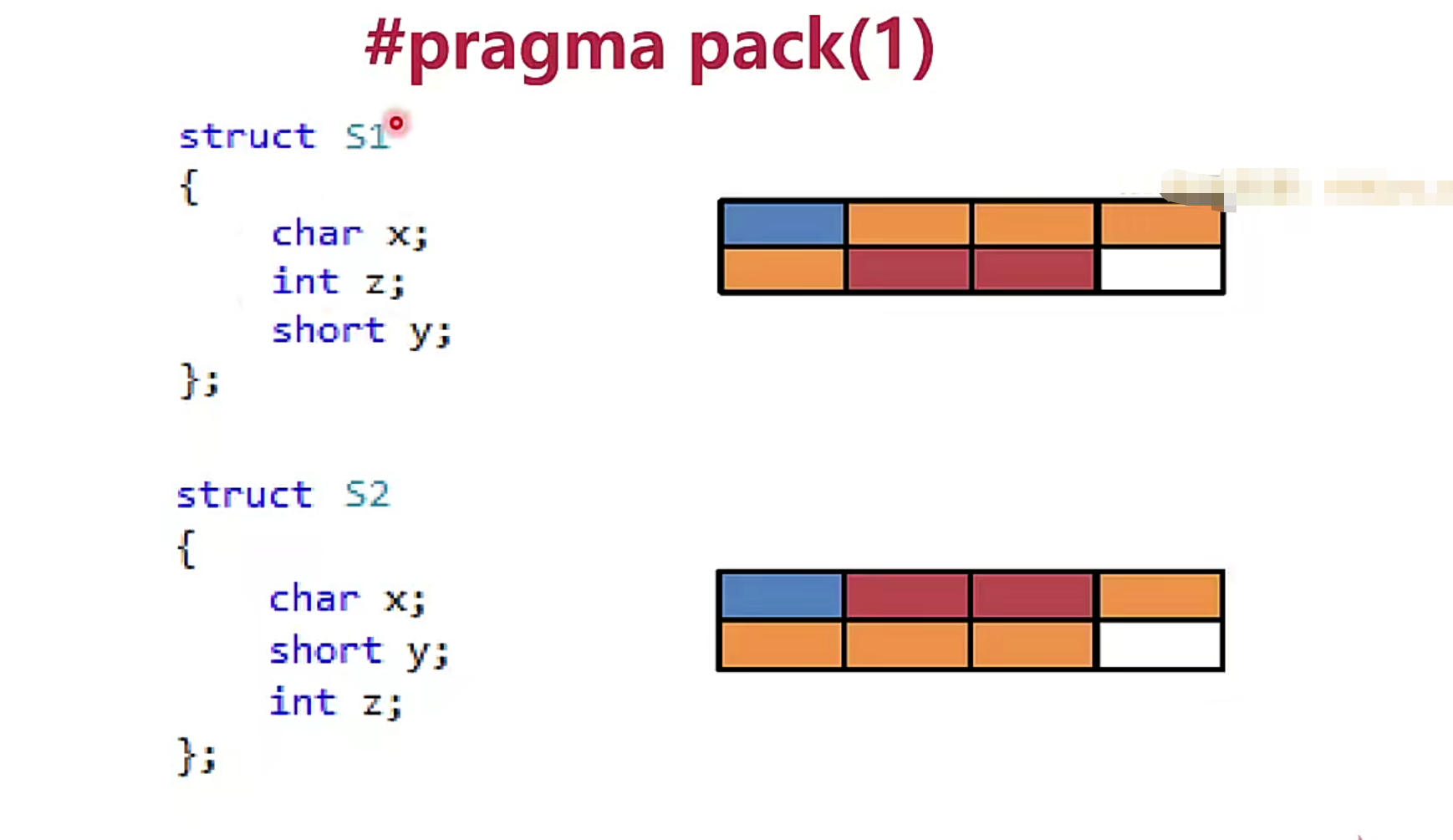
- 原则1:小于等于4字节的变量,两个变量累加的空间大于4的整数倍,就分配4的整数倍+1,反之,没有超过4的整数倍,就分配4的整数倍(例如char:1, int :4,一个4字节分配不了,就开辟两个4字节空间)
- 原则2:大于4字节的变量,以此变量为整数进行分配,原理与以4字节为整数进行分配一致

- 内存布局的4字节的处理,即,每4字节1段,即使char,short分别占1字节和2字节,也要分配4字节
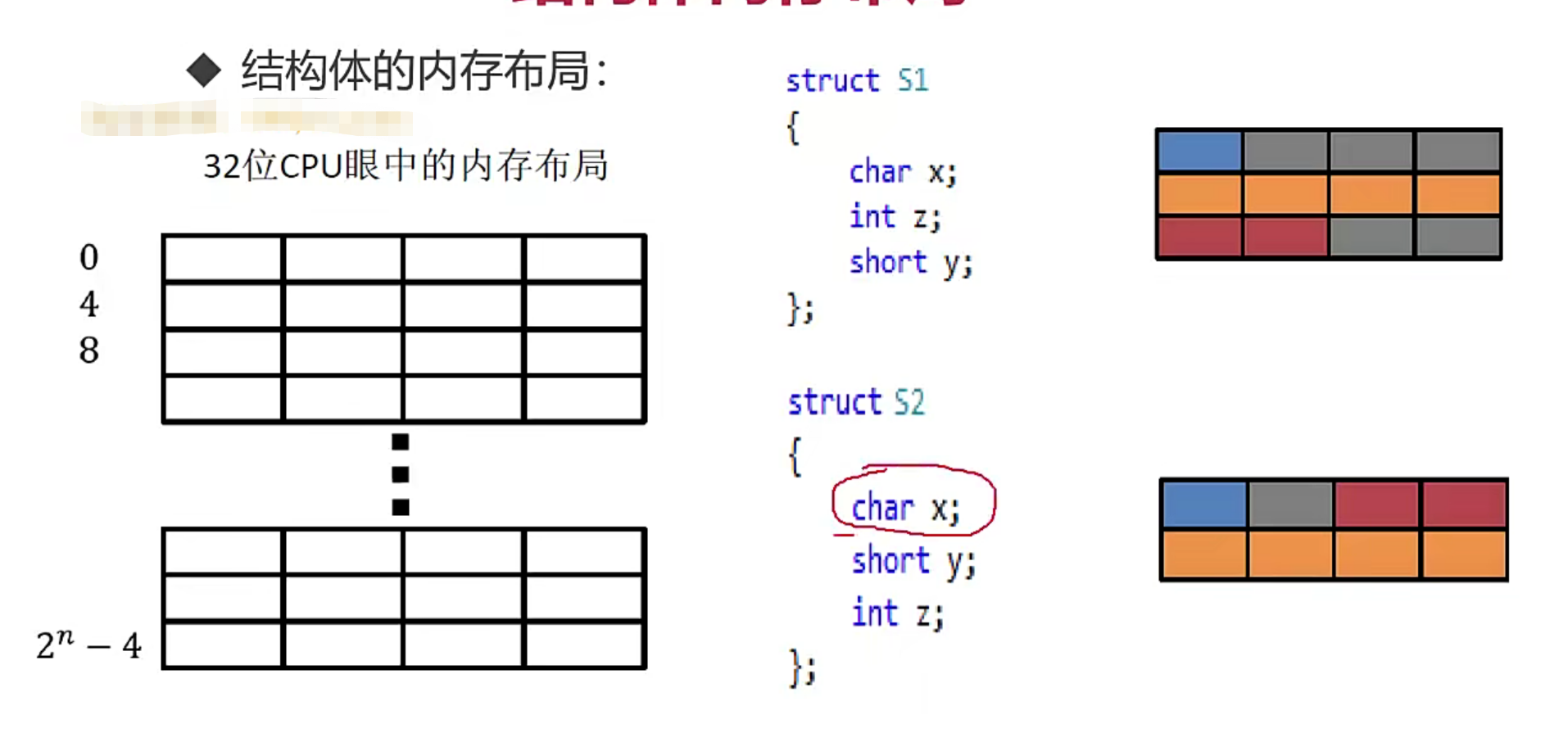
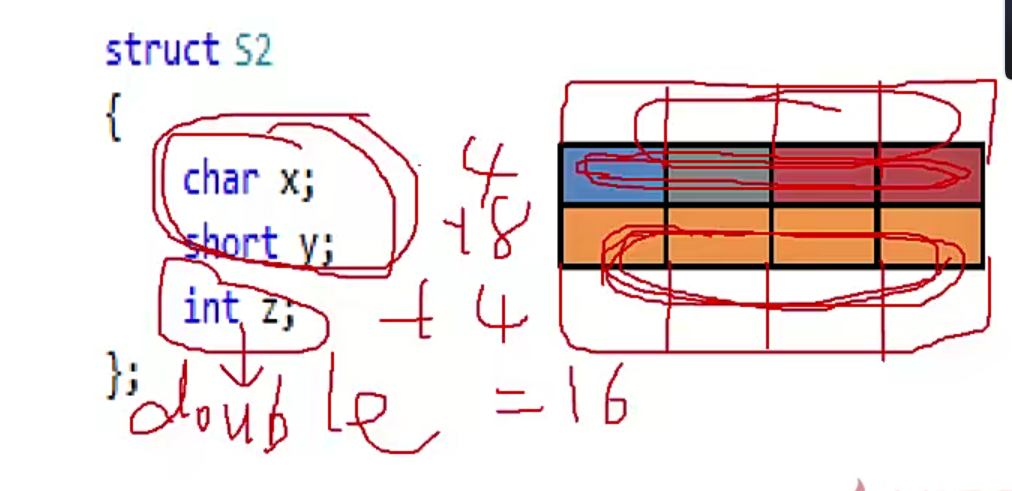
- 最大元素的整数倍的处理:最大元素内存对齐,假如int类型改为占8字节的double类型,S2要共占16字节
- 调试测试
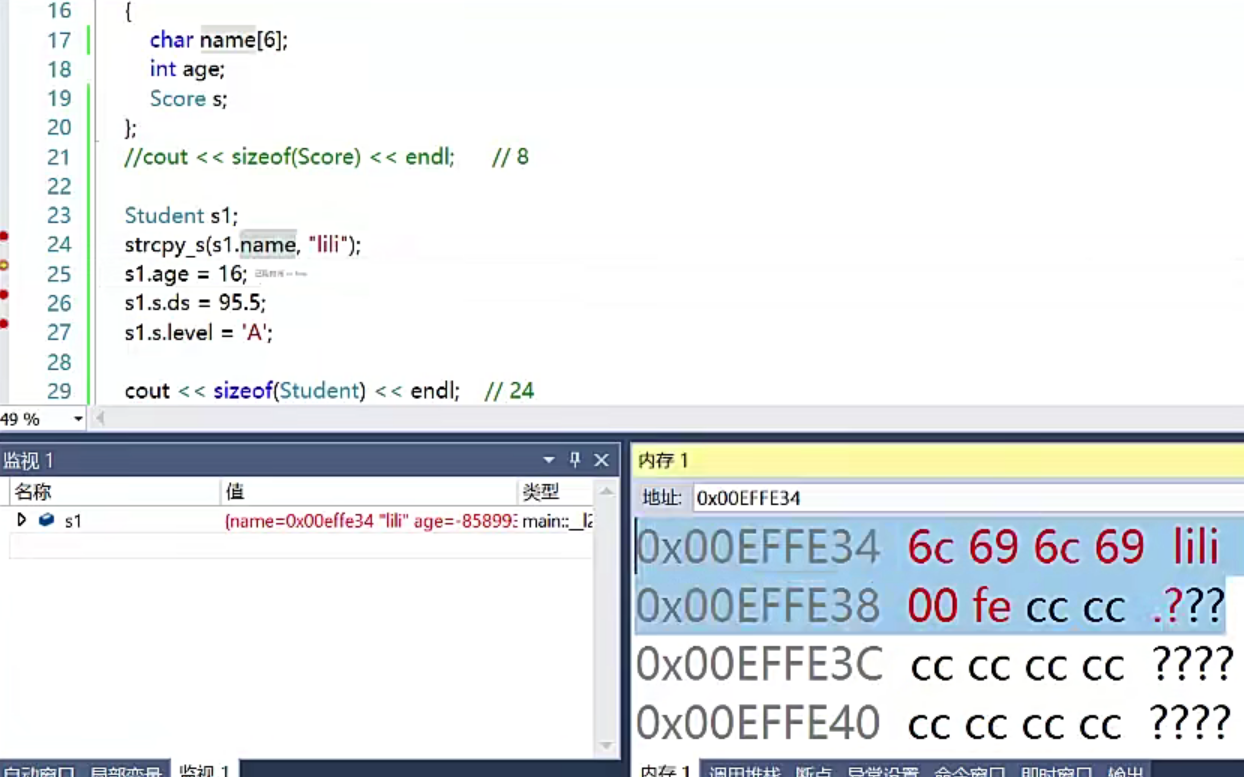
Student s1;
strcpy_s(s1.name, "lili");
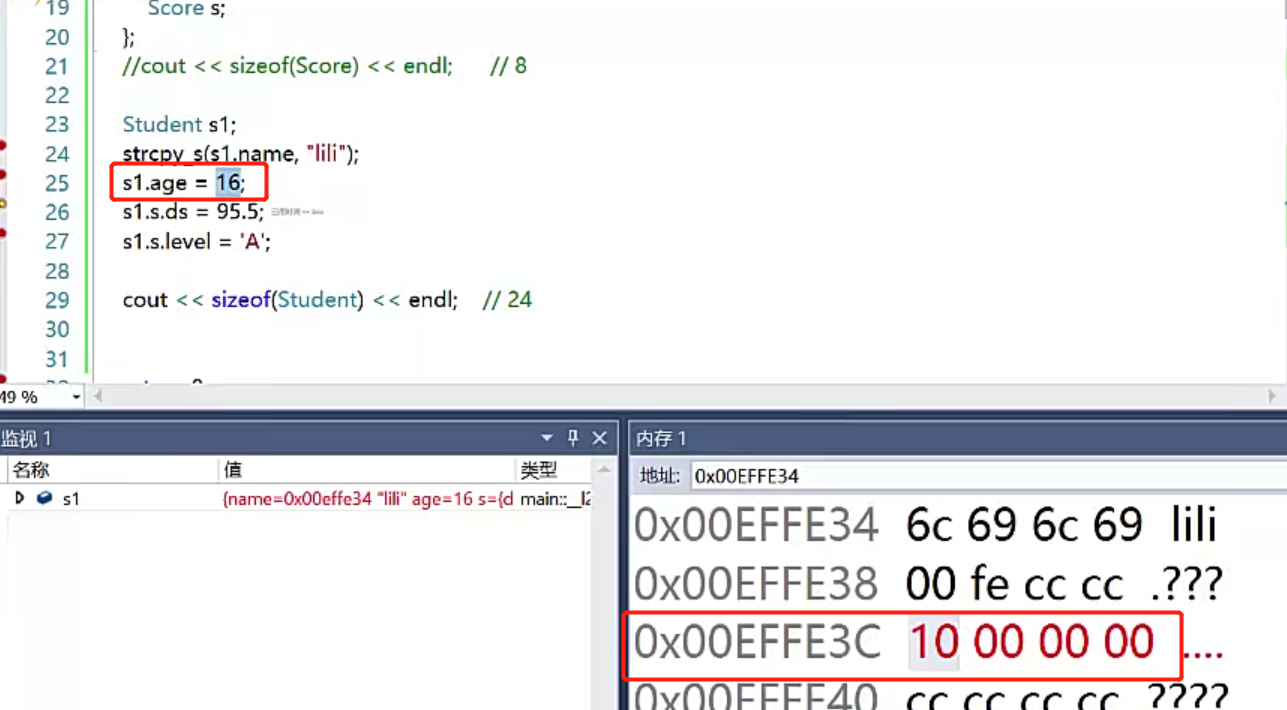
s1.age = 16;
s1.s.ds = 95.5;
s1.s.level = 'A';
cout << sizeof(Student) << endl; // 24 18
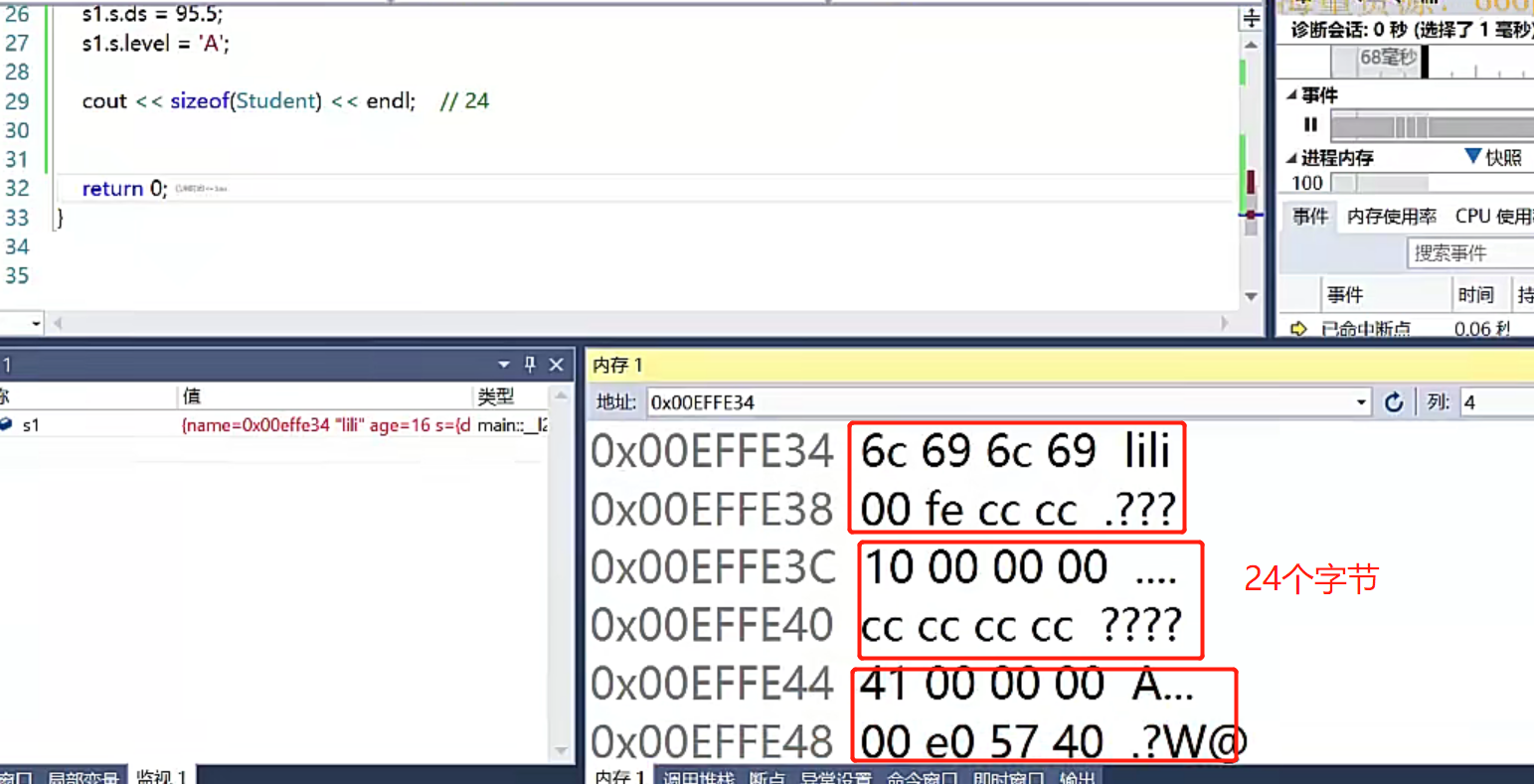
- 总结:

// 设置成连续分配空间
#pragma pack(1)
3. 循环结构
三种循环结构

反汇编查看三种结构效率
- do-while循环代码相对效率较高,只有一个跳转
// do-while语句
sum = 0;
002A1810 mov dword ptr [sum],0
index = 1;
002A1817 mov dword ptr [index],1
do
{
sum += index;
002A181E mov eax,dword ptr [sum]
002A1821 add eax,dword ptr [index]
002A1824 mov dword ptr [sum],eax
index += 1;
002A1827 mov eax,dword ptr [index]
002A182A add eax,1
002A182D mov dword ptr [index],eax
} while (index <= 100);
002A1830 cmp dword ptr [index],64h
002A1834 jle main+7Eh (02A181Eh) // 比较小于0,跳回原循环体
- while循环:两次跳转
// while语句
int sum = 0;
002A17BE mov dword ptr [sum],0
int index = 1;
002A17C5 mov dword ptr [index],1
while (index <= 100)
002A17CC cmp dword ptr [index],64h // 与100比较
002A17D0 jg main+46h (02A17E6h) // g:大于0,就跳出循环到另个位置
{
sum += index;
002A17D2 mov eax,dword ptr [sum]
002A17D5 add eax,dword ptr [index]
002A17D8 mov dword ptr [sum],eax
index += 1;
002A17DB mov eax,dword ptr [index]
002A17DE add eax,1
002A17E1 mov dword ptr [index],eax // 跳回到最初的位置
}
002A17E4 jmp main+2Ch (02A17CCh)
- for循环:三次跳转,相对复杂些,但代码灵活些
// for语句
//index = 1;
sum = 0;
002A17E6 mov dword ptr [sum],0
for (index = 1; index <= 100; ++index)
002A17ED mov dword ptr [index],1
002A17F4 jmp main+5Fh (02A17FFh) // 跳到cmp比较操作
002A17F6 mov eax,dword ptr [index]
002A17F9 add eax,1
002A17FC mov dword ptr [index],eax
002A17FF cmp dword ptr [index],64h
002A1803 jg main+70h (02A1810h) // 与while循环一样,跳出循环
{
sum += index;
002A1805 mov eax,dword ptr [sum]
{
sum += index;
002A1808 add eax,dword ptr [index]
002A180B mov dword ptr [sum],eax
}
002A180E jmp main+56h (02A17F6h) // 跳到index++操作
实例:输出所有形如aabb的四位数的完全平方数
方案1: 构造aabb数,再判断
// aabb的完全平方数
// 先构造aabb,再开方,判断开方后的数是否为整数,相差处理
int n = 0;
double m = 0;
for (size_t a = 1; a < 10; a++) // size_t 是一些C/C++标准在stddef.h中定义的,size_t 类型表示C中任何对象所能达到的最大长度,它是无符号整数
{
for (size_t b = 0; b < 10; b++)
{
n = a * 1100 + b * 11; //aabb
// 难点是,开方后的数如何判断是整数:形如4.0, 5.0等
m = sqrt(n);
// 方案1:相差
if (m - int(m) < 0.00000001)
{
cout << n << endl;
}
}
}
方案2:反向操作:先算出平方和,再判断是否为aabb结构
int high, low; // 高位aa, 地位bb
// aabb的完全平方数
for (size_t index = 31; ; index++) // 小于1000跳过
{
n = index*index;
if (n < 1000)
continue; // 继续下一次循环
if (n > 9999)
break; // 退出循环
high = n / 100; // 4567/100 = 45
low = n % 100; // 4567%100 = 67
if ((high / 10 == high % 10) && (low / 10 == low % 10)) // 判断aa, bb
{
cout << n << endl;
}
}
2. 函数
1. 总览

2. 函数组成


3. 指向函数的指针与返回指针的函数

// demo6-7.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <iostream>
using namespace std;
int MaxValue(int x, int y)
{
return (x > y) ? x : y;
}
int MinValue(int x, int y)
{
return (x < y) ? x : y;
}
int Add(int x, int y)
{
return x+y;
}
bool ProcessNum(int x, int y, int(*p)(int a, int b))
{
cout << p(x, y) << endl;
return true;
}
int main()
{
int x = 10, y = 20;
cout << ProcessNum(x, y, MaxValue) << endl; // 直接传递函数名称即可,指针可以指向
cout << ProcessNum(x, y, MinValue) << endl;
cout << ProcessNum(x, y, Add) << endl;
return 0;
}

4. 命名空间

// stdafx.h : 标准系统包含文件的包含文件,
// 或是经常使用但不常更改的
// 特定于项目的包含文件
//
#pragma once
#include "targetver.h"
#include <stdio.h>
#include <tchar.h>
// TODO: 在此处引用程序需要的其他头文件
int test(int a);
int test(double a);
int test(int a=1, double b=2.0);
namespace quickzhao
{
int test(int a);
}
#include "stdafx.h"
int main()
{
int(*p)(int);
p = test;
int result = (*p)(1);
result = quickzhao::test(1);
result = test(2.0);
result = test(1, 2.0);
return 0;
}
5. 函数体调用过程
#include "stdafx.h"
int MaxValue(int a, int b)
{
return (a > b) ? a : b;
}
int main()
{
int x = 3, y = 4;
MaxValue(x, y);
return 0;
}
- main函数调用过程
// main函数处理过程
int main()
{
// 初始化栈
00C01690 push ebp // 放进栈-寄存器-edp在栈底,esp寄存器在栈顶
00C01691 mov ebp,esp // 将ebb数据放进esp中
00C01693 sub esp,0C0h // 对esp信息做了一个减法 ,这样栈顶与栈底形成一个0C0h空间
00C01699 push ebx
00C0169A push esi // 压栈后,esp地址会继续减少,保持在栈顶
00C0169B push edi
00C0169C lea edi,[ebp-0C0h]
00C016A2 mov ecx,30h
00C016A7 mov eax,0CCCCCCCCh
00C016AC rep stos dword ptr es:[edi]
return 0;
00C016AE xor eax,eax
}
/ 清空栈
009C16D0 pop edi
009C16D1 pop esi
009C16D2 pop ebx
}
009C16D3 mov esp,ebp
009C16D5 pop ebp
009C16D6 ret
- 自定义函数调用过程
/ 自定义函数处理过程
int MaxValue(int a, int b)
{
009C1690 push ebp
009C1691 mov ebp,esp
009C1693 sub esp,0C4h
009C1699 push ebx
009C169A push esi
009C169B push edi
009C169C lea edi,[ebp-0C4h]
009C16A2 mov ecx,31h
009C16A7 mov eax,0CCCCCCCCh
009C16AC rep stos dword ptr es:[edi]
return (a > b) ? a : b;
009C16AE mov eax,dword ptr [a]
009C16B1 cmp eax,dword ptr [b]
009C16B4 jle MaxValue+31h (09C16C1h)
009C16B6 mov ecx,dword ptr [a]
009C16B9 mov dword ptr [ebp-0C4h],ecx
009C16BF jmp MaxValue+3Ah (09C16CAh)
009C16C1 mov edx,dword ptr [b]
009C16C4 mov dword ptr [ebp-0C4h],edx
009C16CA mov eax,dword ptr [ebp-0C4h]
}
int x = 3, y = 4; // 压栈方式,从右往左
00CC166E mov dword ptr [x],3
00CC1675 mov dword ptr [y],4
MaxValue(x, y);
00CC167C mov eax,dword ptr [x]
00CC167F cmp eax,dword ptr [y]
00CC1682 jle main+3Fh (0CC168Fh)
00CC1684 mov ecx,dword ptr [x]
00CC1687 mov dword ptr [ebp-0DCh],ecx
00CC168D jmp main+48h (0CC1698h)
00CC168F mov edx,dword ptr [y]
00CC1692 mov dword ptr [ebp-0DCh],edx
return 0;
00CC1698 xor eax,eax
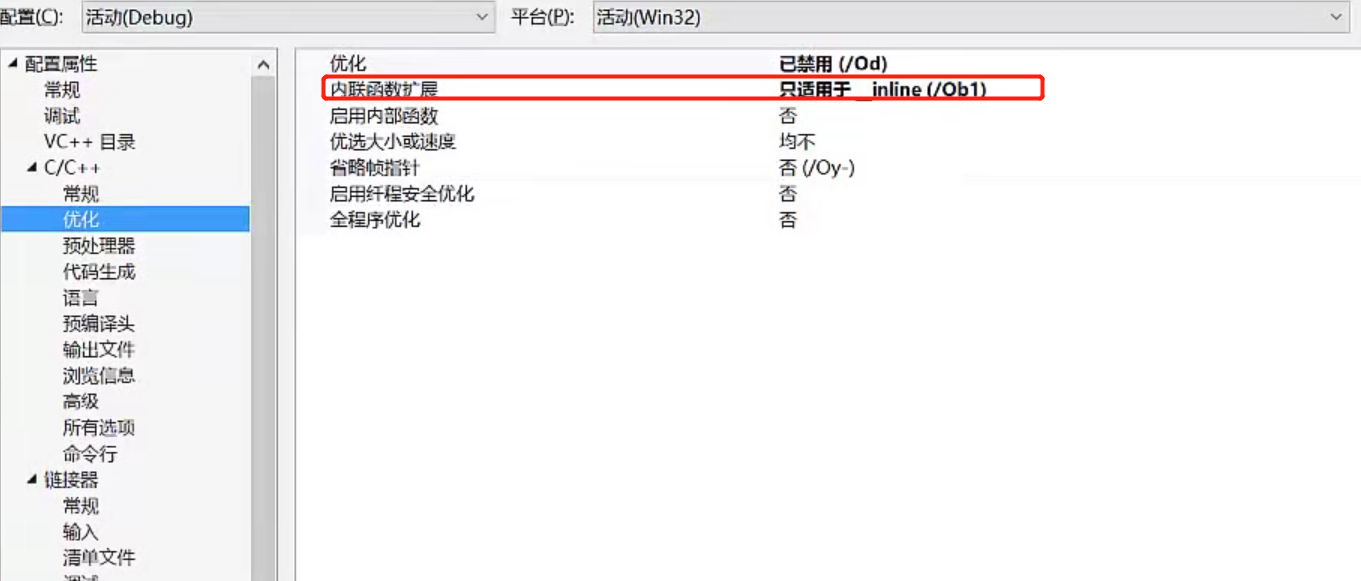
6. 内联函数
- 只处理核心逻辑,不处理堆栈,寄存器等其他处理过程,提高效率
- 内联只是建议,不一定有效,编译器会有自己的优化

VS设置
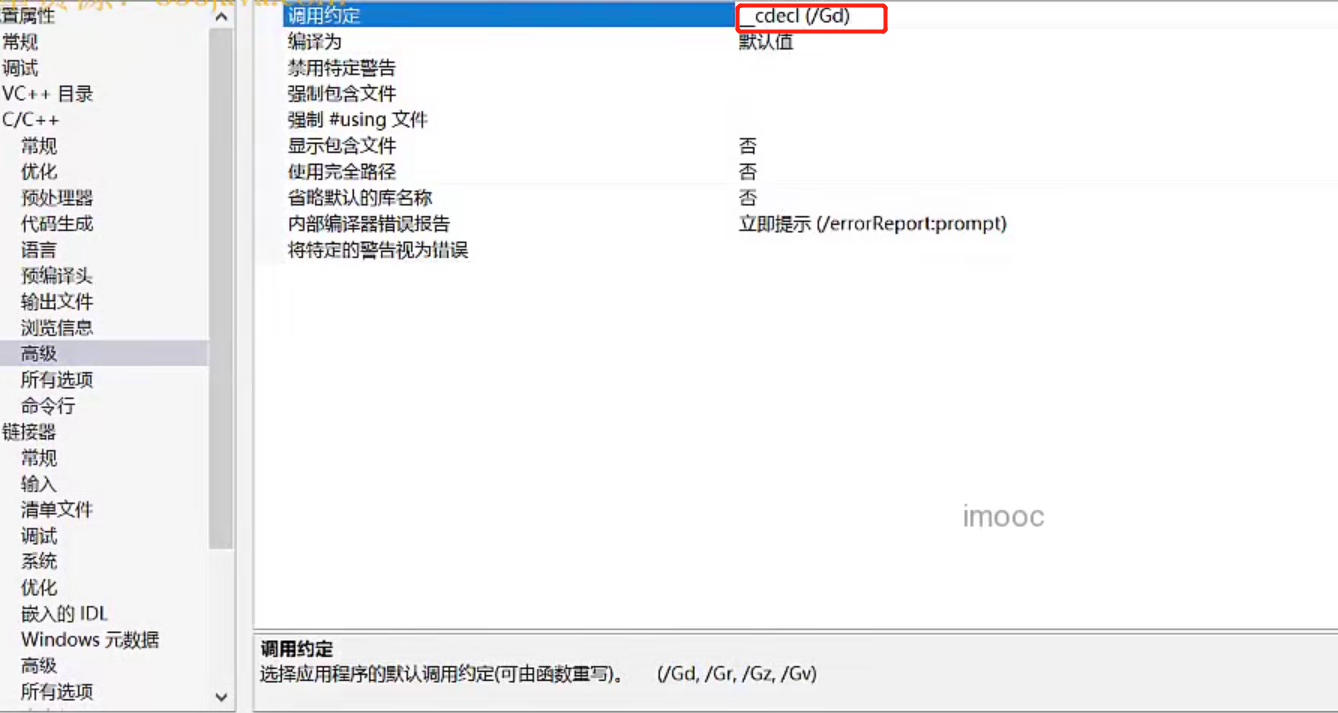
汇编过程
- 将核心过程映射到函数调用处
MaxValue(x, y);
00CC167C mov eax,dword ptr [x]
00CC167F cmp eax,dword ptr [y]
00CC1682 jle main+3Fh (0CC168Fh)
00CC1684 mov ecx,dword ptr [x]
00CC1687 mov dword ptr [ebp-0DCh],ecx
00CC168D jmp main+48h (0CC1698h)
00CC168F mov edx,dword ptr [y]
00CC1692 mov dword ptr [ebp-0DCh],edx
Fib(5);
011238A8 mov eax,5
011238AD test eax,eax
011238AF jne main+55h (011238B5h)
011238B1 jmp main+85h (011238E5h)
011238B3 jmp main+85h (011238E5h)
011238B5 mov ecx,5
011238BA cmp ecx,1
011238BD jne main+63h (011238C3h)
011238BF jmp main+85h (011238E5h)
011238C1 jmp main+85h (011238E5h)
011238C3 mov edx,5
011238C8 sub edx,1
011238CB push edx
011238CC call Fib (0112132Ah) // 当函数复杂时,还是call了内联函数
011238D1 add esp,4
011238D4 mov eax,5
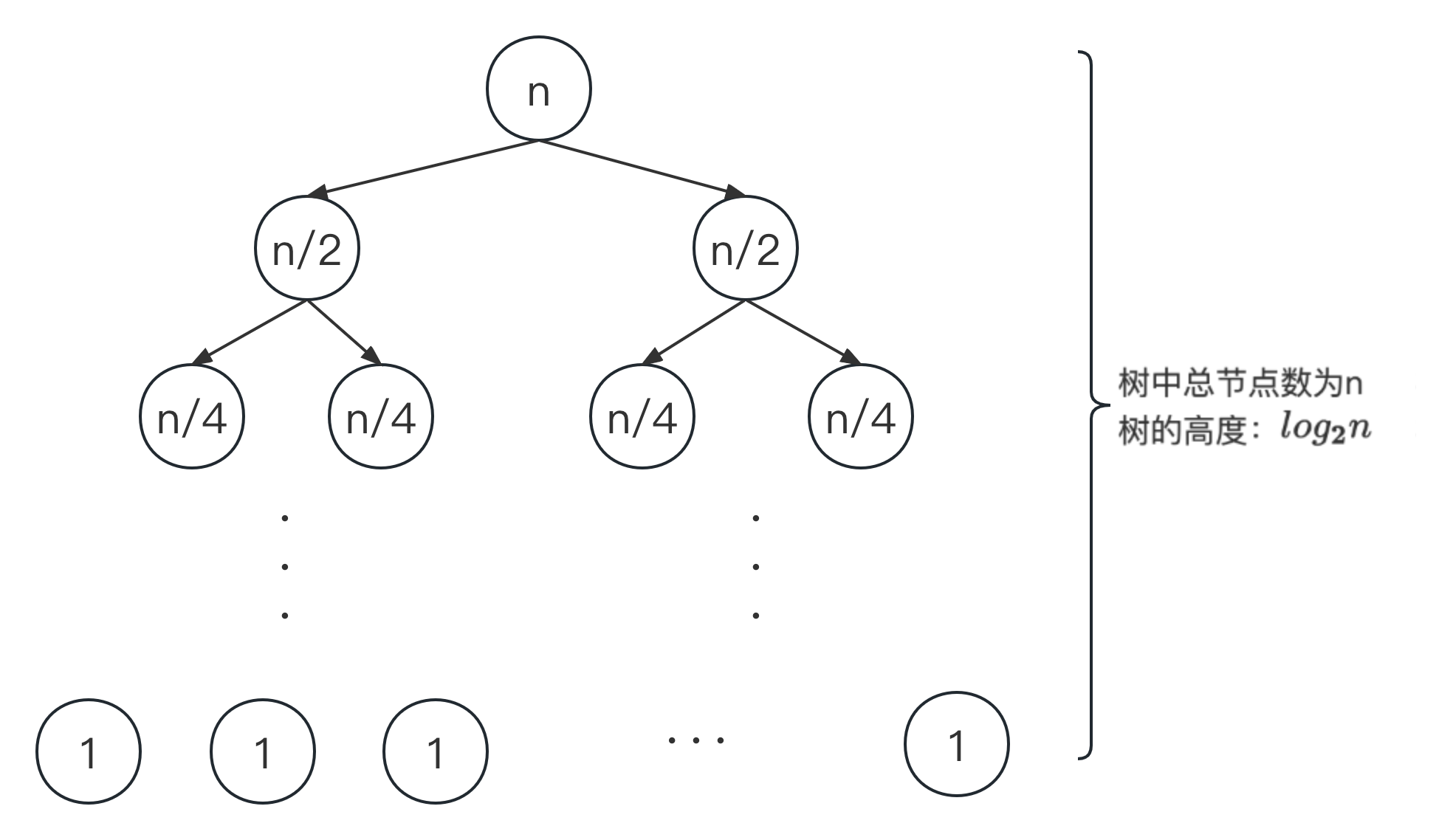
3. 递归
1. 递归与数学归纳法

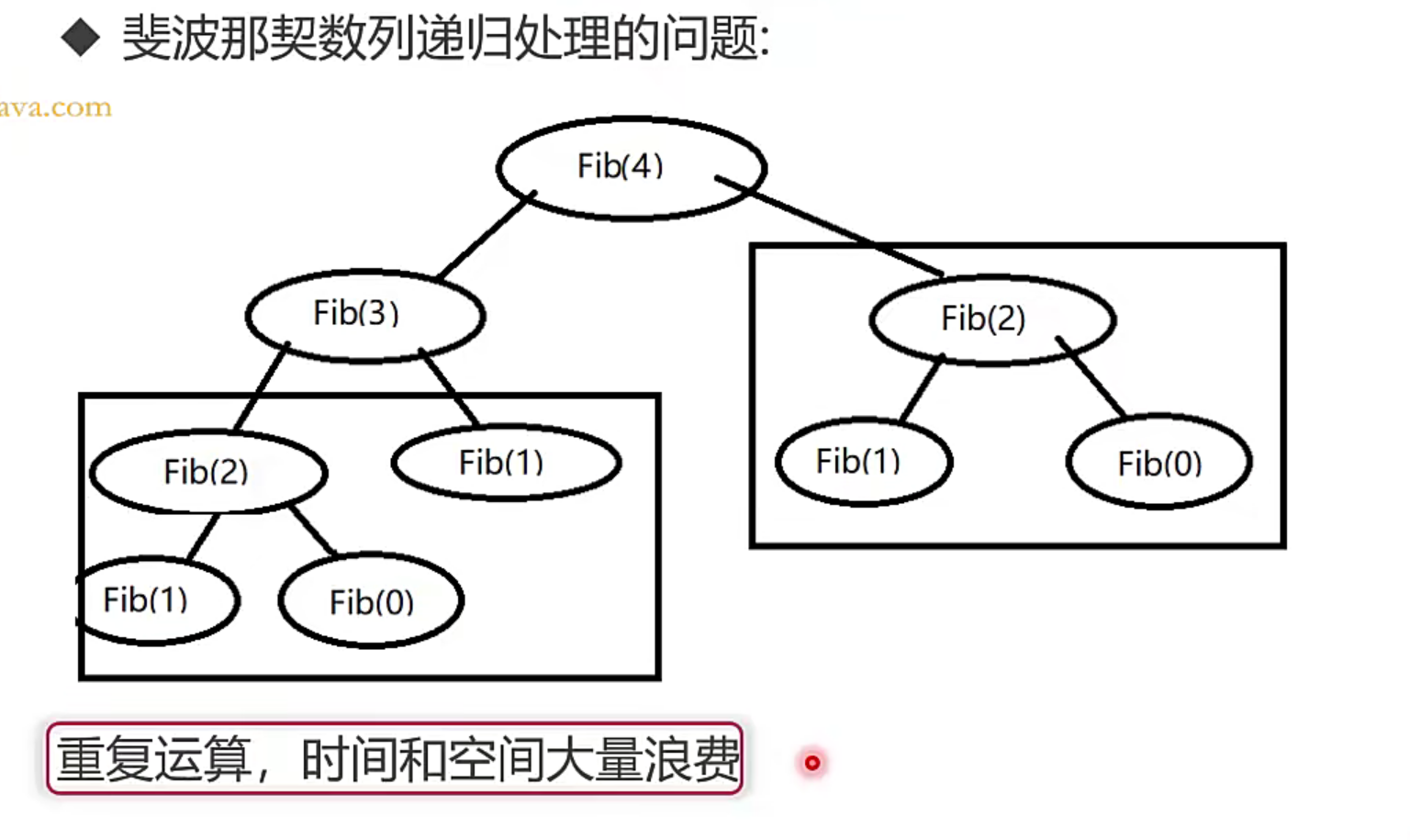
基本法则

递归的缺陷

递归的优化
循环迭代
// 循环
int Fib3(int n)
{
if (n < 2)
{
return n;
}
int n0 = 0, n1 = 1;
int temp;
for (int i = 2; i <= n; i++)
{
temp = n0; // temp记录f(n-2)
n0 = n1; // n1记录f(n-1),用n0传递,是下轮的f(n-2)
n1 = temp + n1; // n1记录这轮的f(n),是下轮的f(n-1)
}
return n1;
}
尾递归
- 最后一步递归调用,之前的栈和寄存器都没有变化
// 尾递归
int Fib2(int n, int ret0, int ret1)
{
if (n == 0)
{
return ret0;
}
else if (n == 1)
{
return ret1;
}
return Fib2(n - 1, ret1, ret0 + ret1);
}
动态规划
int g_a[1000]; // 全局的数组,记录斐波那契数列的前1000个值
// 动态规划
int Fib4(int n)
{
//assert(n >= 0);
g_a[0] = 0;
g_a[1] = 1;
for (int i = 2; i <= n; i++)
{
if (g_a[i] == 0) // 用表记录斐波拉系数,没有就计算,有的话直接用
{
g_a[i] = g_a[i - 1] + g_a[i - 2];
}
}
return g_a[n];
}