题目

BM70 兑换零钱(一)
描述
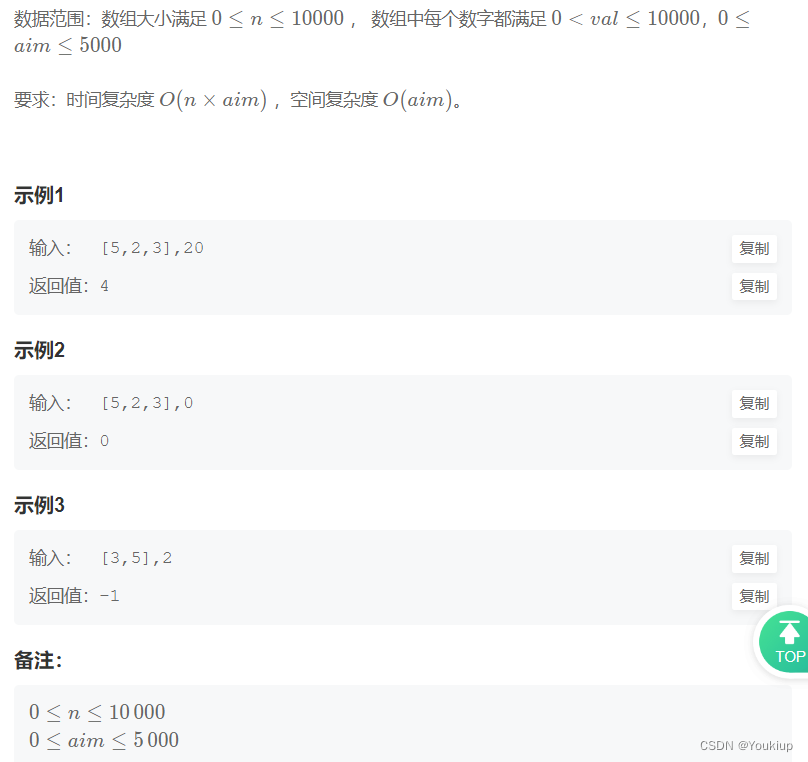
给定数组arr，arr中所有的值都为正整数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个aim，代表要找的钱数，求组成aim的最少货币数。
如果无解，请返回-1.

分析

背包问题，动态规划解决

dp[i]：凑够金额为i所需要的最少货币数

可以使用动态规划的原因：dp[i]的值可以由dp[i-j]+1得到，j为某一货币的面值，相当于i-j所需要的最少货币数加上面值为j的一张货币得到金额为i的最少货币数

因为货币面值为正整数，所以面值为aim所需最多货币数为aim（都使用面值为1的货币），所以初始化的值要大于aim，设为aim+1或者inf都可

最后根据dp[aim]是否小于aim判断是否有解

代码

class Solution:
    def minMoney(self , arr: List[int], aim: int) -> int:
        # write code here
        # 初始化dp ,dp[i]：凑够i所需的最少货币数
        dp = [(aim+1) for i in range(aim+1)]
        dp[0]=0
        # 遍历所有的金额
        for i in range(aim+1):
            # 遍历所有的面值
            for j in arr:
                if j <= i:
                    dp[i] = min(dp[i], dp[i-j] + 1)
        if dp[aim] > aim:
            return -1
        return dp[aim]