贪心算法-数组跳跃游戏(mid)

news2025/11/4 12:18:45

一、问题描述

二、解题思路

1.回溯法

使用递归的方式，找到所有可能的走步方式，并记录递归深度（也就是走步次数），当走完数组时更新最小步长并返回。

这种方式的缺点就是耗时很长，还容易产生栈溢出的问题。

2.贪心算法

直接通过画图来说明一下过程，找局部最优解扩展到全局最优解：

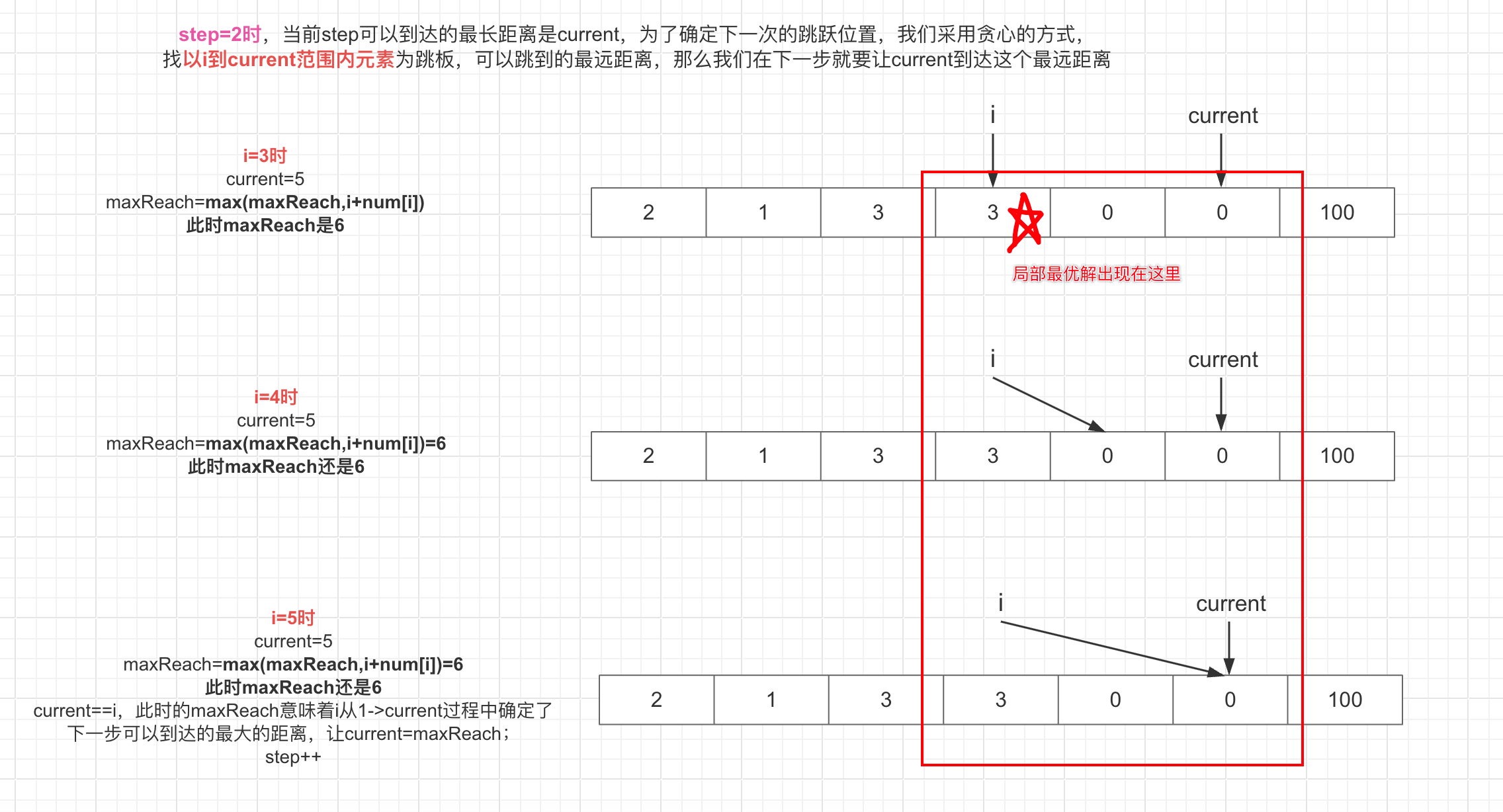
这里注意：当 i >=maxReach时，说明不能到达数组末尾，返回-1

这里可以用下面的示例按照上面的执行过程模拟一下，理解一下到达不了数组末尾是一个什么过程。

三、代码实现

1.回溯法实现

import java.util.*;

public class Solution {
    int minstep=-1;
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @return int整型
     */
    public int minJumpStep (int[] nums) {
        // 首先对常见的几种场景进行判断
        if(nums.length==0||(nums.length>1&&nums[0]==0)){
            return -1;
        }else if(nums.length==1){
            return 0;
        }

        //使用回溯法
        findMinStep(nums,0,0);
        return minstep;
    }
    //回溯法对所有可能的情况进行判断
    public void findMinStep(int[] nums,int nowIndex,int steps){
        if(nowIndex>=nums.length-1){
            if(minstep==-1){
                minstep=steps;
            }else{
                minstep=Math.min(minstep,steps);
            }
            return;
        }
        if(nums[nowIndex]==0){
            return;
        }else{
            for(int i=1;i<=nums[nowIndex];i++){
                findMinStep(nums,nowIndex+i,steps+1);
            } 
        }
        
    }
}

2.贪心算法实现

import java.util.*;

public class Solution {
    int minstep=-1;
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @return int整型
     */
    public int minJumpStep (int[] nums) {
        // 首先对常见的几种场景进行判断
        if(nums.length==0||(nums.length>1&&nums[0]==0)){
            return -1;
        }else if(nums.length==1){
            return 0;
        }

        //使用贪心算法
        //定义变量：
        //nowstep 记录当前走了多少步
        //current 记录nowstep可以走到的最远距离
        //maxReach 记录走到current后到下一次更新step之前可以到达的最远距离
        //初始时，步数为1，走一步以后所在位置nums[0]，最远可到达nums[0]
        int nowstep=1,current=nums[0],maxReach=nums[0];
        for(int i=1;i<nums.length;i++){
            maxReach=Math.max(maxReach,i+nums[i]);
            if(i>=maxReach){
                return -1;
            }
            if(current>=nums.length-1){
                break;
            }
            if(i==current){
                nowstep++;
                current=maxReach;
            }
        }
        return nowstep;

    }

}