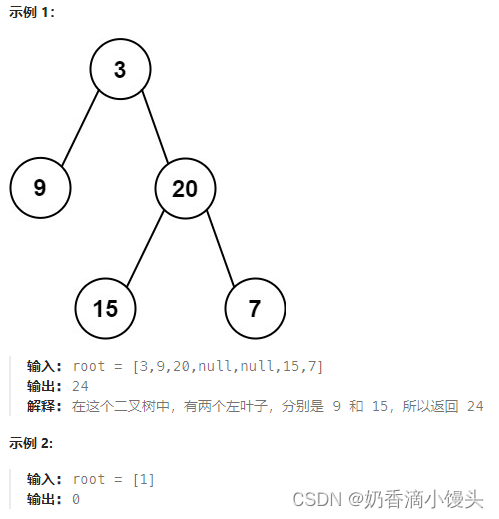
题目（leecode T404）：

给定二叉树的根节点 root ，返回所有左叶子之和。

方法：

迭代法：计算所有的左叶子节点，那我们就必然要找到所有的左叶子节点。那么怎么找呢？如何针对cur->left == NULL&&cur->right ==NULL的话只能判断当前节点是叶子节点，而无法判断出具体是左还是右。因此我们需要从左叶子节点的父节点进行判断，即cur->left != NULL&&cur->left == NULL&&cur->right ==NULL,这样的节点的左孩子结点就是一个左叶子节点。我们这样就确定好了找到左叶子节点的判断逻辑。下面分析迭代的三部曲。

1：确定传入的参数和返回值，传入的参数就是要处理的树节点，返回值是左叶子节点的数值之和，因此需要为int，进行迭代累加得到的就是做叶子节点的和。

2：确定终止条件，当我们遍历到了空节点时，肯定是没有左孩子结点了，就需要终止。

3：确定单层的处理逻辑，当我们找到了左叶子节点时，就记录左叶子节点的值，同时递归根节点的左右子树，最后将两值相加即可得到该树的左叶子节点之和。

题解：

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        if(root == NULL) return 0;            //终止逻辑

        int leftValue = sumOfLeftLeaves(root->left);     //递归左子树
        if(root->left != NULL && root->left->left == NULL && root->left->right == NULL){  //找到左叶子节点就记录其数值
            leftValue = root->left->val;
        }

        int rightValue = sumOfLeftLeaves(root->right);    //递归右子树

        int sum = leftValue + rightValue;
        return sum;
    }
};