难度：中等

题目：

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1 。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b 。
网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。
给你这个计算机网络的初始布线 connections ，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

---

示例 1：

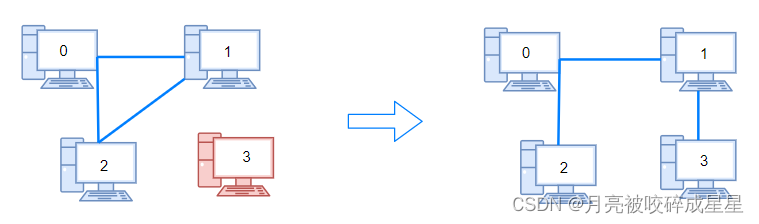
输入：n = 4, connections = [[0,1],[0,2],[1,2]]

输出：1

解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

---

示例 2：

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]

输出：2

---

示例 3：

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]

输出：-1

解释：线缆数量不足。

---

示例 4：

输入：n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]

输出：0

---

提示：

• 1 <= n <= 10^5

• 1 <= connections.length <= min(n*(n-1)/2, 10^5)

• connections[i].length == 2

• 0 <= connections[i][0], connections[i][1] < n

• connections[i][0] != connections[i][1]

• 没有重复的连接。

• 两台计算机不会通过多条线缆连接。

---

Related Topics

• 深度优先搜索

• 广度优先搜索

• 并查集

• 图

---

重点！！！解题思路

第一步：

明确解题手段
类似于此种连通性问题均能使用并查集来实现

第二步：

首先明确缆线数量只能比计算机数量少1，
遍历数组使用并查集连接节点
操作次数=连通分量-1

class UnionFind {
    //记录每个节点的根节点
    int[] parent;
    //记录每个子集的节点数
    int[] rank;
    //记录并查集中的联通分量数量
    int count;

    public UnionFind(int n){
        count=n;
        parent=new int[n];
        for (int i=0;i<n;i++){
            parent[i]=i;
        }
        rank=new int[n];
        Arrays.fill(rank,1);
    }

    //路径压缩
    public int find(int ind){
        if (parent[ind]!=ind){
            parent[ind]=find(parent[ind]);
        }
        return parent[ind];
    }

    //按秩合并
    public void unite(int ind1,int ind2){
        int root1=find(ind1),root2=find(ind2);
        if (root1!=root2){
            if (rank[root1]<rank[root2]){
                int temp=root2;
                root2=root1;
                root1=temp;
            }
            parent[root2]=root1;
            rank[root1]+=rank[root2];
            count--;
        }
    }

    public int getCount(){
        return count;
    }
    public boolean connected(int ind1,int ind2){
        return find(ind1)==find(ind2);
    }
}
class Solution {
    public int makeConnected(int n, int[][] connections) {
        if (n-1>connections.length) return -1;
        UnionFind uf = new UnionFind(n);
        for (int[] connection : connections) {
            uf.unite(connection[0],connection[1]);
        }
        return uf.count-1;
    }
}

解题结果：

如果您还有什么疑问或解答有问题，可在下方评论，我会及时回复。

系列持续更新中，点个订阅吧