给你一个数组 points ，其中 points[i] = [xi, yi] ，表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。

同时给你一个数组 queries ，其中 queries[j] = [xj, yj, rj] ，表示一个圆心在 (xj, yj) 且半径为 rj 的圆。

对于每一个查询 queries[j] ，计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上 ，我们同样认为它在圆 内 。

请你返回一个数组 answer ，其中 answer[j]是第 j 个查询的答案。

示例 1：

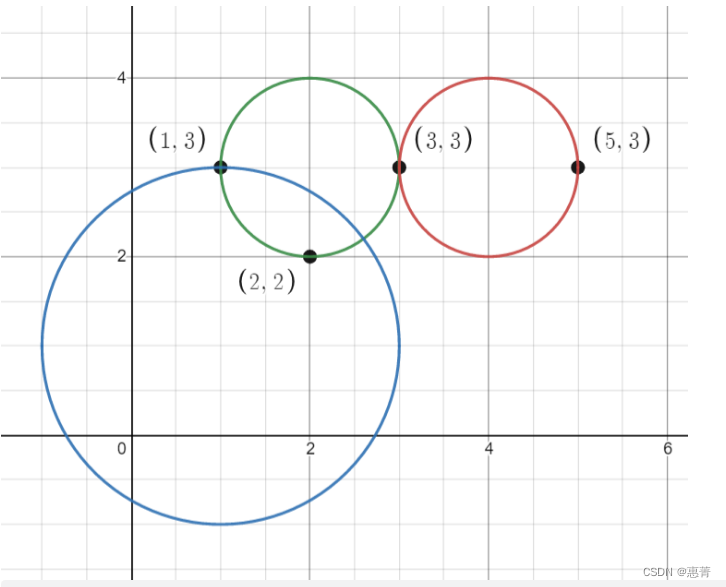
输入：points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
输出：[3,2,2]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆。
示例 2：

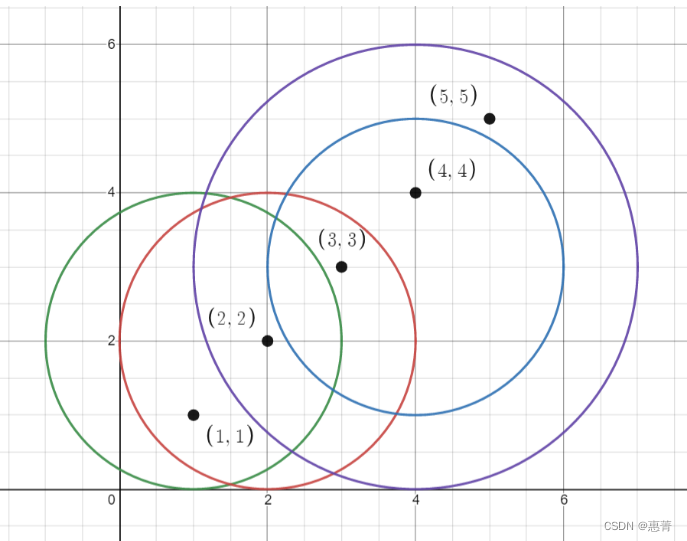
输入：points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出：[2,3,2,4]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆，queries[3] 是紫色的圆。

提示：

1 <= points.length <= 500
points[i].length == 2
0 <= x​​​​​​i, y​​​​​​i <= 500
1 <= queries.length <= 500
queries[j].length == 3
0 <= xj, yj <= 500
1 <= rj <= 500
所有的坐标都是整数。

public int[] countPoints(int[][] points, int[][] queries) {
        int length = queries.length;
        int[] res = new int[length];
        int index=0;
        for (int[] query : queries) {
            int sum=0;
            for (int[] point : points) {
                int x=query[0]-point[0];
                int y=query[1]-point[1];
                if (x*x+y*y<=query[2]*query[2]){
                    sum++;
                }
            }
            res[index++]=sum;
        }
        return res;
    }

func countPoints(points [][]int, queries [][]int) []int {
	res := make([]int,len(queries))
	for index, query := range queries {
		sum:=0
		for _, point := range points {
			x:=query[0]-point[0]
			y:=query[1]-point[1]
			if x*x+y*y<=query[2]*query[2]{
				sum++
			}
		}
		res[index]=sum
	}
	return res
}