树状数组

树状数组 (Binary Indexed Tree(B.I.T), Fenwick Tree) 是一个查询和修改复杂度都为 log(n) 的数据结构。
「前缀和查询」与「单点更新」
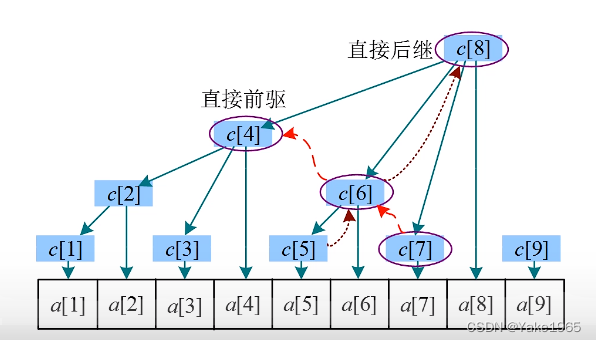
直接前驱：c[i] 的直接前驱为 c[i - lowbid(i)]，即 c[i] 左侧紧邻的子树的根。
直接后继：c[i] 的直接前驱为 c[i + lowbid(i)]，即 c[i] 的父结点。
前驱：c[i] 左侧所有子树的根。
后继：c[i] 的所有祖先。

在这里插入图片描述

307. 区域和检索 - 数组可修改

单点更新，区间求和。

class NumArray {    
    int lowbit(int x) {return x & -x;}
    int query(int i) {
        int ans = 0;
        for (; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    void add(int i, int u) {
        for (; i <= n; i += lowbit(i)) tree[i] += u;
    }

    int[] nums, tree;
    int n;
    public NumArray(int[] _nums) {
        nums = _nums;
        n = nums.length;
        tree = new int[n + 1];
        for (int i = 0; i < n; i++) add(i + 1, nums[i]);
    }
    
    public void update(int i, int val) {
        add(i + 1, val - nums[i]);
        nums[i] = val;
    }
    
    public int sumRange(int l, int r) {
        return query(r + 1) - query(l);
    }
}

时间复杂度：add 操作和 query 的复杂度都是 O(logn)，因此构建数组的复杂度为 O(nlogn)。整体复杂度为 O(nlogn)
空间复杂度：O(n)

315. 计算右侧小于当前元素的个数

「离散化」：把原序列的值域映射到一个连续的整数区间，并保证它们的偏序关系不变。

逆序遍历 nums 读取排名；
先查询严格小于当前排名的「前缀和」，即严格小于当前排名的元素的个数，「前缀和查询」；
给「当前排名」加 1，「单点更新」。

class Solution {
    public List<Integer> countSmaller(int[] nums) {
        List<Integer> res = new ArrayList();
        int n = nums.length;
        discrete(nums);
        BIT bit = new BIT(n);
        for (int i = n - 1; i >= 0; i--) {             
            int j = nums[i];
            bit.update(j + 1, 1);    
            res.add(bit.query(j));            
        }
        Collections.reverse(res);
        return res;
    }
    
    // 离散化 改变了原数组，偏序关系不变。
    void discrete(int[] nums) {
        int n = nums.length;
        int[] tmp = Arrays.copyOf(nums,  n);
        Arrays.sort(tmp);
        for (int i = 0; i < n; i++) {
            nums[i] = Arrays.binarySearch(tmp, nums[i]);
        }
    }
    
    // 数状数组模板
    class BIT {
        private int[] tree;
        private int n;

        public BIT(int n) {
            this.n = n;
            tree = new int[n + 1];
        }
        
        // 单点更新 
        public void update(int i, int delta) {            
            for (; i <= n; i += lowbit(i))  tree[i] += delta;
        }
        
        // 区间查询 前缀和
        public int query(int i) {
            int sum = 0;
            for (; i > 0; i -= lowbit(i)) sum += tree[i];
            return sum;
        }

        int lowbit(int x) {
            return x & (-x);
        }
    }
}

218. 天际线问题

327. 区间和的个数

树状数组（离散化）
由于区间和的定义是子数组的元素和，容易想到「前缀和」来快速求解。

对于每个 nums[i] 而言，需要统计以每个 nums[i] 为右端点的合法子数组个数（合法子数组是指区间和值范围为 [lower, upper] 的子数组）。

可以从前往后处理 nums，假设当前处理到位置 k，同时下标 [0, k] 的前缀和为 s，那么以 nums[k] 为右端点的合法子数组个数，等价于在下标 [0, k - 1] 中前缀和范围在 [s - upper, s - lower] 的数的个数。

需要使用一个数据结构来维护「遍历过程中的前缀和」，每遍历 nums[i] 需要往数据结构加一个数，同时每次需要查询值在某个范围内的数的个数。涉及的操作包括「单点修改」和「区间查询」，容易想到使用树状数组进行求解。

但值域的范围是巨大的（同时还有负数域），可以利用 nums 的长度为 10⁵ 来做离散化。需要考虑用到的数组都有哪些：

首先前缀和数组中的每一位 s 都需要被用到（添加到树状数组中）；
同时对于每一位 nums[i]（假设对应的前缀和为 s），我们都需要查询以其为右端点的合法子数组个数，即查询前缀和范围在 [s - upper, s - lower] 的数的个数。
因此对于前缀和数组中的每一位 s，我们用到的数有 s、s - upper 和 s - lower 三个数字，共有 1e51e5 个 ss，即最多共有 3×10⁵ 个不同数字被使用，我们可以对所有用到的数组进行排序编号（离散化），从而将值域大小控制在 3×10⁵ 范围内。

class Solution {
    int m;
    int[] tree = new int[100010 * 3];
    int lowbit(int x) {
        return x & -x;
    }
    void add(int x, int v) {
        for (int i = x; i <= m; i += lowbit(i)) tree[i] += v;
    }
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    public int countRangeSum(int[] nums, int lower, int upper) {
        Set<Long> set = new HashSet<>();
        long s = 0;
        set.add(s);
        for (int i : nums) {
            s += i;
            set.add(s);
            set.add(s - lower);
            set.add(s - upper);
        }
        List<Long> list = new ArrayList<>(set);
        Collections.sort(list);
        Map<Long, Integer> map = new HashMap<>();
        for (long x : list) map.put(x, ++m);
        s = 0;
        int ans = 0;
        add(map.get(s), 1);
        for (int i : nums) {
            s += i;
            int a = map.get(s - lower), b = map.get(s - upper) - 1;
            ans += query(a) - query(b);
            add(map.get(s), 1);
        }
        return ans;
    }
}

406. 根据身高重建队列

493. 翻转对

673. 最长递增子序列的个数

1157. 子数组中占绝大多数的元素

1395. 统计作战单位数

class Solution {    
    public int numTeams(int[] rating) {
        int n = rating.length;
        discrete(rating);
        int ans = 0;
        BIT bit = new BIT(n);
        for (int i = 0; i < n; i++) {
            int x = rating[i];            
            int frontSmall = bit.query(x); // 前面比x小的个数
            int frontLarge = i - frontSmall; // 前面比x大的个数 
            int backSmall = x - frontSmall;
            int backLarge = n - 1 - i - backSmall;
            ans += frontSmall * backLarge + frontLarge * backSmall;
            bit.update(x + 1, 1); // 对应 tree 需要 + 1
        }
        return ans;
    }
    
    // 离散化 改变了原数组，偏序关系不变。
    void discrete(int[] nums) {
        int n = nums.length;
        int[] tmp = Arrays.copyOf(nums,  n);
        Arrays.sort(tmp);
        for (int i = 0; i < n; i++) {
            nums[i] = Arrays.binarySearch(tmp, nums[i]);
        }
    }
    
    // 数状数组模板
    class BIT {
        private int[] tree;
        private int n;

        public BIT(int n) {
            this.n = n;
            tree = new int[n + 1];
        }
        
        // 单点更新 
        public void update(int i, int delta) {            
            for (; i <= n; i += lowbit(i))  tree[i] += delta;
        }
        
        // 区间查询 前缀和
        public int query(int i) {
            int sum = 0;
            for (; i > 0; i -= lowbit(i)) sum += tree[i];
            return sum;
        }

        int lowbit(int x) {
            return x & (-x);
        }
    }
}