博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持!
博主链接
本人就职于国际知名终端厂商,负责modem芯片研发。
在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。
博客内容主要围绕:
5G/6G协议讲解
算力网络讲解(云计算,边缘计算,端计算)
高级C语言讲解
Rust语言讲解
使用cub库优化分布式计算下的原子操作

我们以 Jacobi 迭代的拉普拉斯方程求解器为例进行讲解。下面简单介绍以下算法,我们不需要深入了解这个算法的含义。
1. 拉普拉斯方程
有限元/有限体积/有限差分应用中的一个常见主题是使用松弛方法求解椭圆偏微分方程。 也许最简单的椭圆偏微分方程是拉普拉斯方程: ▽ 2 f = 0 \bigtriangledown^{2}f = 0 ▽2f=0。其中, ▽ 2 = ▽ ∗ ▽ \bigtriangledown^{2} = \bigtriangledown *\bigtriangledown ▽2=▽∗▽ 是拉普拉斯算子(所有坐标方向的二阶导数之和), 𝑓=𝑓(𝐫) 为标量场,是空间矢量坐标 𝐫 的函数。例如,拉普拉斯方程可以用来求解边缘被加热到固定温度的金属板上的温度平衡分布。
在一维的 𝑓=𝑓(𝑥) 情况下,此方程为: α 2 α x 2 f = 0 \frac{\alpha^{2}}{\alpha x^{2}} f = 0 αx2α2f=0。
假设我们想在给定固定边界条件 𝑓(0)=𝑇left 和 𝑓(𝐿)=𝑇right 下,在域 𝑥=[0,𝐿] 上求解这个方程。也就是说,我们想知道作为 𝑥 的函数,温度在 𝑥 取值域内的分布情况。一种常见的方法是将空间离散为 𝑁 个点的集合,这些点位于 0,𝐿/(𝑁−1),2𝐿/(𝑁−1),…,(𝑁−2)𝐿/(𝑁−1),𝐿 。最左侧和最右侧的点将分别保持在固定温度 𝑇left 和 𝑇right ,而内部的 𝑁−2 点的温度是我们需要求解的未知数。这些点之间的距离是 Δ𝑥=𝐿/(𝑁−1) ,我们将这些点存储在一个长度为 𝑁 的数组中。对于(零索引的)数组中的每个索引 𝑖 ,其坐标位置为 𝑖𝐿/(𝑁−1)=𝑖Δ𝑥 。
在离散空间域中,索引 𝑖 处的场导数是附近点的函数。例如,一阶导数的一个简单的离散形式是: α 2 α x 2 f i = ( f i + 1 − f i − 1 ) / ( 2 Δ 𝑥 ) \frac{\alpha^{2}}{\alpha x^{2}} f_{i} = (f_{i+1} - f_{i-1}) / (2Δ𝑥) αx2α2fi=(fi+1−fi−1)/(2Δx)。
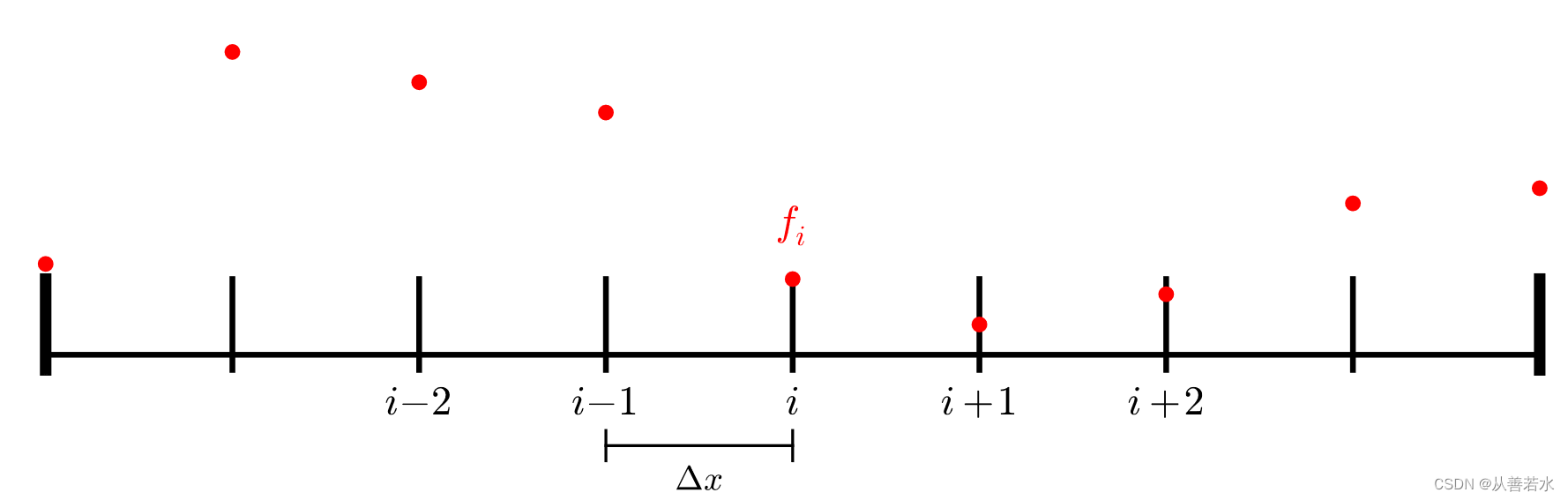
而二阶导数的简单的离散形式是:
α
2
α
x
2
f
i
=
(
f
i
+
1
−
2
f
i
+
f
i
−
1
)
/
(
Δ
𝑥
2
)
\frac{\alpha^{2}}{\alpha x^{2}} f_{i} = (f_{i+1} - 2f_{i} + f_{i-1}) / (Δ𝑥^{2})
αx2α2fi=(fi+1−2fi+fi−1)/(Δx2)
如果我们让这个表达式等于 0 来满足拉普拉斯方程,我们得到: f i + 1 − 2 f i + f i − 1 = 0 f_{i+1} - 2f_{i} + f_{i-1} = 0 fi+1−2fi+fi−1=0
通过对 𝑓𝑖 的求解,我们得到: f i = ( f i + 1 + f i − 1 ) / 2 f_{i} = (f_{i+1} + f_{i-1})/2 fi=(fi+1+fi−1)/2
2. Jacobi 迭代求解
尽管 𝑓𝑖+1 和 𝑓𝑖−1 也在变化(边界点 𝑖==0 和 𝑖==𝑁−1 除外),我们只需在这个解之上为 𝑓𝑖 迭代 多次,直到解达到充分均衡。也就是说,如果在每次迭代中我们都采用 𝑓 的旧解来计算两个相邻点的平均值,并以此作为新解中的每个点,我们最终将求解出 𝑓 的平衡分布。
以(串行)伪代码描述这种方法:
while (error > tolerance):
l2_norm = 0
for i = 1, N-2:
f[i] = 0.5 * (f_old[i-1] + f_old[i+1])
l2_norm += (f[i] - f_old[i]) * (f[i] - f_old[i])
error = sqrt(l2_norm / N)
swap(f_old, f)
3. 单 GPU 的 CUDA 实现
cuda代码实现如下:
#include <iostream>
#include <limits>
#include <cstdio>
inline void CUDA_CHECK (cudaError_t err) {
if (err != cudaSuccess) {
fprintf(stderr, "CUDA error: %s\n", cudaGetErrorString(err));
exit(-1);
}
}
#define NUM_POINTS 4194304
#define TOLERANCE 0.0001
#define MAX_ITERS 1000
__global__ void jacobi (const float* f_old, float* f, float* l2_norm, int N)
{
int idx = threadIdx.x + blockIdx.x * blockDim.x;
if (idx > 0 && idx < N - 1) {
f[idx] = 0.5f * (f_old[idx+1] + f_old[idx-1]);
float l2 = (f[idx] - f_old[idx]) * (f[idx] - f_old[idx]);
atomicAdd(l2_norm, l2);
}
}
__global__ void initialize (float* f, float T_left, float T_right, int N)
{
int idx = threadIdx.x + blockIdx.x * blockDim.x;
if (idx == 0) {
f[idx] = T_left;
}
else if (idx == N - 1) {
f[idx] = T_right;
}
else if (idx < N - 1) {
f[idx] = 0.0f;
}
}
int main() {
// 为“旧”数据的网格数据和临时缓冲区
// 分配空间。
float* f_old;
float* f;
CUDA_CHECK(cudaMalloc(&f_old, NUM_POINTS * sizeof(float)));
CUDA_CHECK(cudaMalloc(&f, NUM_POINTS * sizeof(float)));
// 在主机和设备上为 L2 范数分配内存。
float* l2_norm = (float*) malloc(sizeof(float));
float* d_l2_norm;
CUDA_CHECK(cudaMalloc(&d_l2_norm, sizeof(float)));
// 将误差初始化为较大的数字。
float error = std::numeric_limits<float>::max();
// 初始化数据。
int threads_per_block = 256;
int blocks = (NUM_POINTS + threads_per_block - 1) / threads_per_block;
float T_left = 5.0f;
float T_right = 10.0f;
initialize<<<blocks, threads_per_block>>>(f_old, T_left, T_right, NUM_POINTS);
initialize<<<blocks, threads_per_block>>>(f, T_left, T_right, NUM_POINTS);
CUDA_CHECK(cudaDeviceSynchronize());
// 现在进行迭代,直到误差足够小为止。
// 限制迭代次数,将其用作一种安全机制。
int num_iters = 0;
while (error > TOLERANCE && num_iters < MAX_ITERS) {
// 将范数数据初始化为零
CUDA_CHECK(cudaMemset(d_l2_norm, 0, sizeof(float)));
// 启动核函数进行计算
jacobi<<<blocks, threads_per_block>>>(f_old, f, d_l2_norm, NUM_POINTS);
CUDA_CHECK(cudaDeviceSynchronize());
// 交换 f_old 和 f
std::swap(f_old, f);
// 更新主机范数;通过按区域数进行规范化并取平方根来计算误差
CUDA_CHECK(cudaMemcpy(l2_norm, d_l2_norm, sizeof(float), cudaMemcpyDeviceToHost));
if (*l2_norm == 0.0f) {
// 处理第一次迭代
error = 1.0f;
}
else {
error = std::sqrt(*l2_norm / NUM_POINTS);
}
if (num_iters % 10 == 0) {
std::cout << "Iteration = " << num_iters << " error = " << error << std::endl;
}
++num_iters;
}
if (error <= TOLERANCE && num_iters < MAX_ITERS) {
std::cout << "Success!\n";
}
else {
std::cout << "Failure!\n";
}
// 清理
free(l2_norm);
CUDA_CHECK(cudaFree(d_l2_norm));
CUDA_CHECK(cudaFree(f_old));
CUDA_CHECK(cudaFree(f));
return 0;
}
代码编译和执行命令:
nvcc -x cu -arch=sm_70 -o jacobi jacobi.cpp
./jacobi
程序执行结果:
Iteration = 0 error = 0.00272958
Iteration = 10 error = 0.00034546
Iteration = 20 error = 0.000210903
Iteration = 30 error = 0.000157015
Iteration = 40 error = 0.000127122
Iteration = 50 error = 0.00010783
Success!
4. 利用 NVSHMEM 在多 GPU 上实现
对于多个 GPU,一个非常简单的分配策略是将域划分为 𝑀 个块(其中 𝑀 为 GPU 的数量)。PE 0 将获得 [0,𝑁/𝑀−1] 内的点,PE 1 将获得 [𝑁/𝑀,2𝑁/𝑀−1] 内的点,以此类推。在这种方法中,PE 之间的通信需要发生在 PE 之间的边界点上。例如,PE0 上点 𝑖=𝑁/𝑀−1 的更新为: 𝑓 [ 𝑁 / 𝑀 − 1 ] = ( 𝑓 [ 𝑁 / 𝑀 ] + 𝑓 [ 𝑁 / 𝑀 − 2 ] ) / 2 𝑓[𝑁/𝑀−1]=(𝑓[𝑁/𝑀]+𝑓[𝑁/𝑀−2]) / 2 f[N/M−1]=(f[N/M]+f[N/M−2])/2。
但此 PE 不包含 𝑖=𝑁/𝑀 的数据点,它属于 PE1。我们需要从远端 PE 获取这个数据点。为此,我们可以使用 nvshmem_float_g() API 来获取远端 PE 上的标量。
float r = nvshmem_float_g(source, target_pe);
结果如下所示。请注意,对于 PE0,位置 N / M对应于 PE1 的索引 0。
f_left = f[N / M - 2]
f_right = nvshmem_float_g(&f[0], 1)
f[N / M - 1] = (f_right + f_left) / 2
代码实现如下:
#include <iostream>
#include <limits>
#include <cstdio>
#include <nvshmem.h>
#include <nvshmemx.h>
inline void CUDA_CHECK (cudaError_t err) {
if (err != cudaSuccess) {
fprintf(stderr, "CUDA error: %s\n", cudaGetErrorString(err));
exit(-1);
}
}
#define NUM_POINTS 4194304
#define TOLERANCE 0.0001
#define MAX_ITERS 1000
__global__ void jacobi (const float* f_old, float* f, float* l2_norm, int N)
{
int idx = threadIdx.x + blockIdx.x * blockDim.x;
int my_pe = nvshmem_my_pe();
int n_pes = nvshmem_n_pes();
// 如果我们为最左侧 PE,且位于最左侧边界点,
// 或者如果我们为最右侧 PE,且位于最右侧边界点
// (因为这些均已固定),则不参与。
bool on_boundary = false;
if (my_pe == 0 && idx == 0) {
on_boundary = true;
}
else if (my_pe == n_pes - 1 && idx == N - 1) {
on_boundary = true;
}
if (idx < N && !on_boundary) {
// 检索旧数据中的左右点。
// 如果我们完全位于本地域内部,
// 这完全是本地访问。否则,我们需
// 连接远程 PE 以获取左点或右点。
float f_left;
float f_right;
if (idx == 0) {
// 请注意,如果 my_pe == 0,我们无法到这一步。
f_left = nvshmem_float_g(&f_old[N - 1], my_pe - 1);
}
else {
f_left = f_old[idx - 1];
}
if (idx == N - 1) {
// 请注意,如果 my_pe == n_pes - 1,我们无法到这一步。
f_right = nvshmem_float_g(&f_old[0], my_pe + 1);
}
else {
f_right = f_old[idx + 1];
}
f[idx] = 0.5f * (f_right + f_left);
float l2 = (f[idx] - f_old[idx]) * (f[idx] - f_old[idx]);
atomicAdd(l2_norm, l2);
}
}
__global__ void initialize (float* f, float T_left, float T_right, int N)
{
int idx = threadIdx.x + blockIdx.x * blockDim.x;
int my_pe = nvshmem_my_pe();
int n_pes = nvshmem_n_pes();
if (idx == 0 && my_pe == 0) {
f[idx] = T_left;
}
else if (idx == N - 1 && my_pe == n_pes - 1) {
f[idx] = T_right;
}
else if (idx < N - 1) {
f[idx] = 0.0f;
}
}
int main() {
// 初始化 NVSHMEM
nvshmem_init();
// 获取 NVSHMEM 处理元素 ID 和 PE 数量
int my_pe = nvshmem_my_pe();
int n_pes = nvshmem_n_pes();
// 每个 PE(任意)选择与其 ID 对应的 GPU
int device = my_pe;
CUDA_CHECK(cudaSetDevice(device));
// 每台设备处理 1 / n_pes 的部分工作。
const int N = NUM_POINTS / n_pes;
// 为“旧”数据的网格数据和临时缓冲区
// 分配空间。
float* f_old = (float*) nvshmem_malloc(N * sizeof(float));
float* f = (float*) nvshmem_malloc(N * sizeof(float));
// 在主机和设备上为 L2 范数分配内存。
float* l2_norm = (float*) malloc(sizeof(float));
float* d_l2_norm = (float*) nvshmem_malloc(sizeof(float));
// 将误差初始化为较大的数字。
float error = std::numeric_limits<float>::max();
// 初始化数据。
int threads_per_block = 256;
int blocks = (N + threads_per_block - 1) / threads_per_block;
float T_left = 5.0f;
float T_right = 10.0f;
initialize<<<blocks, threads_per_block>>>(f_old, T_left, T_right, N);
initialize<<<blocks, threads_per_block>>>(f, T_left, T_right, N);
CUDA_CHECK(cudaDeviceSynchronize());
// 现在进行迭代,直到误差足够小为止。
// 限制迭代次数,将其用作一种安全机制。
int num_iters = 0;
while (error > TOLERANCE && num_iters < MAX_ITERS) {
// 将范数数据初始化为零
CUDA_CHECK(cudaMemset(d_l2_norm, 0, sizeof(float)));
// 启动核函数进行计算
jacobi<<<blocks, threads_per_block>>>(f_old, f, d_l2_norm, N);
CUDA_CHECK(cudaDeviceSynchronize());
// 交换 f_old 和 f
std::swap(f_old, f);
// 对所有 PE 的 L2 范数求和
// 请注意,这是阻塞 API,因此之后不需要任何显式同步
nvshmem_float_sum_reduce(NVSHMEM_TEAM_WORLD, d_l2_norm, d_l2_norm, 1);
// 更新主机范数;通过按区域数进行规范化并取平方根来计算误差
CUDA_CHECK(cudaMemcpy(l2_norm, d_l2_norm, sizeof(float), cudaMemcpyDeviceToHost));
if (*l2_norm == 0.0f) {
// 处理第一次迭代
error = 1.0f;
}
else {
error = std::sqrt(*l2_norm / NUM_POINTS);
}
if (num_iters % 10 == 0 && my_pe == 0) {
std::cout << "Iteration = " << num_iters << " error = " << error << std::endl;
}
++num_iters;
}
if (my_pe == 0) {
if (error <= TOLERANCE && num_iters < MAX_ITERS) {
std::cout << "Success!\n";
}
else {
std::cout << "Failure!\n";
}
}
free(l2_norm);
nvshmem_free(d_l2_norm);
nvshmem_free(f_old);
nvshmem_free(f);
// 最终确定 nvshmem
nvshmem_finalize();
return 0;
}
编译和运行指令:
nvcc -x cu -arch=sm_70 -rdc=true -I $NVSHMEM_HOME/include -L $NVSHMEM_HOME/lib -lnvshmem -lcuda -o jacobi_step1 jacobi_step1.cpp
nvshmrun -np $NUM_DEVICES ./jacobi_step1
执行结果如下:
Iteration = 0 error = 0.00272958
Iteration = 10 error = 0.00034546
Iteration = 20 error = 0.000210903
Iteration = 30 error = 0.000157015
Iteration = 40 error = 0.000127122
Iteration = 50 error = 0.00010783
Success!
5. 使用cub改善归约性能
5.1 上面代码的问题 —— 大量的序列化原子操作
在之前的代码中,数十万个线程对l2_norm进行了原子写入:
int main()
{
...
float* d_l2_norm = (float*) nvshmem_malloc(sizeof(float));
jacobi<<<blocks, threads_per_block>>>(f_old, f, d_l2_norm, N); // 网格启动时有数十万个线程。
}
__global__ void jacobi (const float* f_old, float* f, float* l2_norm, int N)
{
...
float l2 = (f[idx] - f_old[idx]) * (f[idx] - f_old[idx]);
// 在核函数中,(实际上)每个线程都在对称的“l2_norm”中进行原子写入。
atomicAdd(l2_norm, l2);
}
这意味着我们有成百上千的线程对同一个变量执行原子归约。在了解了这一点后,我们可能会提出,在我们的程序中存在大量的原子操作序列化可能会对性能产生重大影响。
5.2 使用 Nsight Compute 进行配置
Nsight Compute 是一个核函数性能分析工具,在这里我们将使用其命令行工具ncu来分析之前的解决方案代码。
profile_one_jacobi_PE.sh作为简单的脚本,仅会分析 PE 0(跳过前几个核函数,让 GPU 预热)。运行以下单元格来编译和运行解决方案的应用程序,为第一个 PE 生成性能分析报告:
profile_one_jacobi_PE.sh的代码如下:
#!/bin/bash
if [ $PMI_RANK -eq 0 ]; then
ncu -s 20 -c 1 -k jacobi -o report -f $@
else
$@
fi
执行命令生成分析报告:
nvcc -x cu -arch=sm_70 -rdc=true -I $NVSHMEM_HOME/include -L $NVSHMEM_HOME/lib -lnvshmem -lcuda -o jacobi_solution_step1 jacobi_step1.cpp
nvshmrun -np $NUM_DEVICES ./profile_one_jacobi_PE.sh ./jacobi_solution_step1
ncu -i report.ncu-rep
Iteration = 0 error = 0.00272958
Iteration = 10 error = 0.00034546
==PROF== Connected to process 27322 (/dli/task/jacobi_solution_step1)
==PROF== Profiling "jacobi": 0%....50%....100%Iteration = 20 error = 0.000210903
Iteration = 30 error = 0.000157015
Iteration = 40 error = 0.000127122
Iteration = 50 error = 0.00010783
Success!
- 19 passes
==PROF== Disconnected from process 27322
==PROF== Report: report.ncu-rep
[27322] jacobi_solution_step1@127.0.0.1
jacobi(float const*, float*, float*, int), 2023-Jan-15 10:34:15, Context 1, Stream 7
Section: GPU Speed Of Light
---------------------------------------------------------------------- --------------- ------------------------------
DRAM Frequency cycle/usecond 876.64
SM Frequency cycle/nsecond 1.31
Elapsed Cycles cycle 3305314
Memory [%] % 1.06
SOL DRAM % 0.24
Duration msecond 2.52
SOL L1/TEX Cache % 0.93
SOL L2 Cache % 1.06
SM Active Cycles cycle 3268283.65
SM [%] % 0.48
---------------------------------------------------------------------- --------------- ------------------------------
WRN This kernel exhibits low compute throughput and memory bandwidth utilization relative to the peak performance
of this device. Achieved compute throughput and/or memory bandwidth below 60.0% of peak typically indicate
latency issues. Look at Scheduler Statistics and Warp State Statistics for potential reasons.
Section: Launch Statistics
---------------------------------------------------------------------- --------------- ------------------------------
Block Size 256
Grid Size 4096
Registers Per Thread register/thread 62
Shared Memory Configuration Size byte 0
Driver Shared Memory Per Block byte/block 0
Dynamic Shared Memory Per Block byte/block 0
Static Shared Memory Per Block byte/block 0
Threads thread 1048576
Waves Per SM 12.80
---------------------------------------------------------------------- --------------- ------------------------------
Section: Occupancy
---------------------------------------------------------------------- --------------- ------------------------------
Block Limit SM block 32
Block Limit Registers block 4
Block Limit Shared Mem block 32
Block Limit Warps block 8
Theoretical Active Warps per SM warp/cycle 32
Theoretical Occupancy % 50
Achieved Occupancy % 39.56
Achieved Active Warps Per SM warp 25.32
---------------------------------------------------------------------- --------------- ------------------------------
我们可以看到,尽管实现了合理占用率(Section:Occupancy -> Achieved Occupancy),我们还是没有接近理论峰值内存带宽(Section: GPU Speed Of Light -> Memory [%])。
这佐证了我们之前的假设,可能是因为我们有数百上千个线程对相同的变量执行原子归约。
5.3 如何降低原子归约操作的序列化
限制原子操作序列化数量的一种方法是在线程内执行尽可能多的归约。在这种方法中,每个线程块将高效地归约其每个线程的l2值,然后令每个线程块只用一个线程为对称的l2_norm变量执行原子加法(Atomic Add)操作。
5.4 使用cub进行线程块级的归约
cub 是一个由 NVIDIA 提供的标头库,作为 CUDA 的一部分,可为内核中常用的原始操作提供接口,如归约和扫描操作。
就目前而言,我们在cub中使用 BlockReduce 接口来执行模块级归约,然后只让每个模块中的线程“0”向对称数据l2_norm执行原子添加。
如要使用cub,我们要先添加文件头:
#include <cub/cub.cuh>
如果使用BlockReduce,接下来我们要定义BlockReduce类型,并按我们的需要配置每个块里的线程数:
typedef cub::BlockReduce<float, 256> BlockReduce;
BlockReduce 将利用共享内存来执行高效的线程块级的归约,所以接下来我们要分配共享内存以供其使用:
__shared__ typename BlockReduce::TempStorage temp_storage;
最后我们要执行归约,在我们的案例中的归约是求和:
float reduced_value = BlockReduce(temp_storage).Sum(value_to_reduce);
5.5 在 Jacobi 代码中使用线程块级的归约
下面的代码,以使用cub执行线程块级的归约,即仅由每个线程块的0号线程在对称的l2_norm上执行原子写入操作,实现如下:
#include <iostream>
#include <limits>
#include <cstdio>
#include <nvshmem.h>
#include <nvshmemx.h>
#include <cub/cub.cuh>
inline void CUDA_CHECK (cudaError_t err) {
if (err != cudaSuccess) {
fprintf(stderr, "CUDA error: %s\n", cudaGetErrorString(err));
exit(-1);
}
}
#define NUM_POINTS 4194304
#define TOLERANCE 0.0001
#define MAX_ITERS 1000
__global__ void jacobi (const float* f_old, float* f, float* l2_norm, int N)
{
int idx = threadIdx.x + blockIdx.x * blockDim.x;
int my_pe = nvshmem_my_pe();
int n_pes = nvshmem_n_pes();
// 如果我们为最左侧 PE,且位于最左侧边界点或者
// 如果我们为最右侧 PE,且位于最右侧边界点
// (因为这些均已固定),则不参与。
bool on_boundary = false;
if (my_pe == 0 && idx == 0) {
on_boundary = true;
}
else if (my_pe == n_pes - 1 && idx == N - 1) {
on_boundary = true;
}
// 如果我们使用 typedef cub::BlockReduce<float, 256> BlockReduce,
// 则使用尽量多线程的块定义 BlockReduce 类型;
typedef cub::BlockReduce<float, 256> BlockReduce;
// 分配共享内存以减少块
__shared__ typename BlockReduce::TempStorage temp_storage;
float l2 = 0.0f;
if (idx < N && !on_boundary) {
// 检索旧数据中的左右点。
// 如果我们完全位于本地域内部,
// 这完全是本地访问。否则,我们需
// 连接远程 PE 以获取左点或右点。
float f_left;
float f_right;
if (idx == 0) {
// 请注意,如果 my_pe == 0,我们无法到这一步。
f_left = nvshmem_float_g(&f_old[N - 1], my_pe - 1);
}
else {
f_left = f_old[idx - 1];
}
if (idx == N - 1) {
// 请注意,如果 my_pe == n_pes - 1,我们无法到这一步。
f_right = nvshmem_float_g(&f_old[0], my_pe + 1);
}
else {
f_right = f_old[idx + 1];
}
f[idx] = 0.5f * (f_right + f_left);
l2 = (f[idx] - f_old[idx]) * (f[idx] - f_old[idx]);
}
// 线程块级的归约(所有线程必须参与)
float block_l2 = BlockReduce(temp_storage).Sum(l2);
// 只有块中的第一个线程执行原子操作
if (threadIdx.x == 0) {
atomicAdd(l2_norm, block_l2);
}
}
__global__ void initialize (float* f, float T_left, float T_right, int N)
{
int idx = threadIdx.x + blockIdx.x * blockDim.x;
int my_pe = nvshmem_my_pe();
int n_pes = nvshmem_n_pes();
if (idx == 0 && my_pe == 0) {
f[idx] = T_left;
}
else if (idx == N - 1 && my_pe == n_pes - 1) {
f[idx] = T_right;
}
else if (idx < N - 1) {
f[idx] = 0.0f;
}
}
int main() {
// 初始化 NVSHMEM
nvshmem_init();
// 获取 NVSHMEM 处理元素 ID 和 PE 数量
int my_pe = nvshmem_my_pe();
int n_pes = nvshmem_n_pes();
// 每个 PE(任意)选择与其 ID 对应的 GPU
int device = my_pe;
CUDA_CHECK(cudaSetDevice(device));
// 每台设备处理 1 / n_pes 的部分工作。
const int N = NUM_POINTS / n_pes;
// 为“旧”数据的网格数据和临时缓冲区
// 分配空间。
float* f_old = (float*) nvshmem_malloc(N * sizeof(float));
float* f = (float*) nvshmem_malloc(N * sizeof(float));
// 在主机和设备上为 L2 范数分配内存。
float* l2_norm = (float*) malloc(sizeof(float));
float* d_l2_norm = (float*) nvshmem_malloc(sizeof(float));
// 将误差初始化为较大的数字。
float error = std::numeric_limits<float>::max();
// 初始化数据。
int threads_per_block = 256;
int blocks = (N + threads_per_block - 1) / threads_per_block;
float T_left = 5.0f;
float T_right = 10.0f;
initialize<<<blocks, threads_per_block>>>(f_old, T_left, T_right, N);
initialize<<<blocks, threads_per_block>>>(f, T_left, T_right, N);
CUDA_CHECK(cudaDeviceSynchronize());
// 现在进行迭代,直到误差足够小为止。
// 限制迭代次数,将其用作一种安全机制。
int num_iters = 0;
while (error > TOLERANCE && num_iters < MAX_ITERS) {
// 将范数数据初始化为零
CUDA_CHECK(cudaMemset(d_l2_norm, 0, sizeof(float)));
// 启动核函数进行计算
jacobi<<<blocks, threads_per_block>>>(f_old, f, d_l2_norm, N);
CUDA_CHECK(cudaDeviceSynchronize());
// 交换 f_old 和 f
std::swap(f_old, f);
// 对所有 PE 的 L2 范数求和
// 请注意,这是阻塞 API,因此之后不需要任何显式同步
nvshmem_float_sum_reduce(NVSHMEM_TEAM_WORLD, d_l2_norm, d_l2_norm, 1);
// 更新主机范数;通过按区域数进行规范化并取平方根来计算误差
CUDA_CHECK(cudaMemcpy(l2_norm, d_l2_norm, sizeof(float), cudaMemcpyDeviceToHost));
if (*l2_norm == 0.0f) {
// 处理第一次迭代
error = 1.0f;
}
else {
error = std::sqrt(*l2_norm / NUM_POINTS);
}
if (num_iters % 10 == 0 && my_pe == 0) {
std::cout << "Iteration = " << num_iters << " error = " << error << std::endl;
}
++num_iters;
}
if (my_pe == 0) {
if (error <= TOLERANCE && num_iters < MAX_ITERS) {
std::cout << "Success!\n";
}
else {
std::cout << "Failure!\n";
}
}
free(l2_norm);
nvshmem_free(d_l2_norm);
nvshmem_free(f_old);
nvshmem_free(f);
// 最终确定 nvshmem
nvshmem_finalize();
return 0;
}
编译和运行命令:
nvcc -x cu -arch=sm_70 -rdc=true -I $NVSHMEM_HOME/include -L $NVSHMEM_HOME/lib -lnvshmem -lcuda -o jacobi_step2 jacobi_step2.cpp
nvshmrun -np $NUM_DEVICES ./jacobi_step2
执行结果如下:
Iteration = 0 error = 0.00272958
Iteration = 10 error = 0.00034546
Iteration = 20 error = 0.000210903
Iteration = 30 error = 0.000157015
Iteration = 40 error = 0.000127122
Iteration = 50 error = 0.00010783
Success!
使用 Nsight Compute 分析性能:
nvshmrun -np $NUM_DEVICES ./profile_one_jacobi_PE.sh ./jacobi_step2
ncu -i report.ncu-rep
输出报告如下:
Iteration = 0 error = 0.00272958
Iteration = 10 error = 0.00034546
==PROF== Connected to process 27395 (/dli/task/jacobi_step2)
==PROF== Profiling "jacobi": 0%....50%....100%Iteration = 20 error = 0.000210903
Iteration = 30 error = 0.000157015
Iteration = 40 error = 0.000127122
Iteration = 50 error = 0.00010783
Success!
- 19 passes
==PROF== Disconnected from process 27395
==PROF== Report: report.ncu-rep
[27395] jacobi_step2@127.0.0.1
jacobi(float const*, float*, float*, int), 2023-Jan-15 11:30:01, Context 1, Stream 7
Section: GPU Speed Of Light
---------------------------------------------------------------------- --------------- ------------------------------
DRAM Frequency cycle/usecond 788.17
SM Frequency cycle/nsecond 1.17
Elapsed Cycles cycle 29534
Memory [%] % 26.50
SOL DRAM % 26.50
Duration usecond 25.15
SOL L1/TEX Cache % 31.73
SOL L2 Cache % 15.39
SM Active Cycles cycle 24447.96
SM [%] % 31.95
---------------------------------------------------------------------- --------------- ------------------------------
WRN This kernel exhibits low compute throughput and memory bandwidth utilization relative to the peak performance
of this device. Achieved compute throughput and/or memory bandwidth below 60.0% of peak typically indicate
latency issues. Look at Scheduler Statistics and Warp State Statistics for potential reasons.
Section: Launch Statistics
---------------------------------------------------------------------- --------------- ------------------------------
Block Size 256
Grid Size 4096
Registers Per Thread register/thread 62
Shared Memory Configuration Size Kbyte 8.19
Driver Shared Memory Per Block byte/block 0
Dynamic Shared Memory Per Block byte/block 0
Static Shared Memory Per Block byte/block 44
Threads thread 1048576
Waves Per SM 12.80
---------------------------------------------------------------------- --------------- ------------------------------
Section: Occupancy
---------------------------------------------------------------------- --------------- ------------------------------
Block Limit SM block 32
Block Limit Registers block 4
Block Limit Shared Mem block 384
Block Limit Warps block 8
Theoretical Active Warps per SM warp/cycle 32
Theoretical Occupancy % 50
Achieved Occupancy % 41.47
Achieved Active Warps Per SM warp 26.54
---------------------------------------------------------------------- --------------- ------------------------------
我们注意到,Section: GPU Speed Of Light -> Memory [%]已得到显著改善,Section: GPU Speed Of Light -> Elapsed Cycles大大降低。有趣的是,我们在Section: Launch Statistics -> Static Shared Memory Per Block中看到了分配给BlockReduce的更有效的归约所使用的共享内存。







![[Android]Shape Drawable](https://img-blog.csdnimg.cn/f4b2bbd2aa4d45d6b0a21575b8bdb9b1.png)