代码随想录算法训练营第15天| 102. 二叉树的层序遍历、226. 翻转二叉树

二叉树的层序遍历

学会二叉树的层序遍历，可以一口气打完以下十题：

102.二叉树的层序遍历
107.二叉树的层次遍历II
199.二叉树的右视图
637.二叉树的层平均值
429.N叉树的层序遍历
515.在每个树行中找最大值
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II
104.二叉树的最大深度
111.二叉树的最小深度

我要打十个

力扣题目链接(opens new window)

给你一个二叉树，请你返回其按层序遍历得到的节点值。（即逐层地，从左到右访问所有节点）。

输出：[[3],[9,20],[15,7]]

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

使用队列实现二叉树广度优先遍历，动画如下：

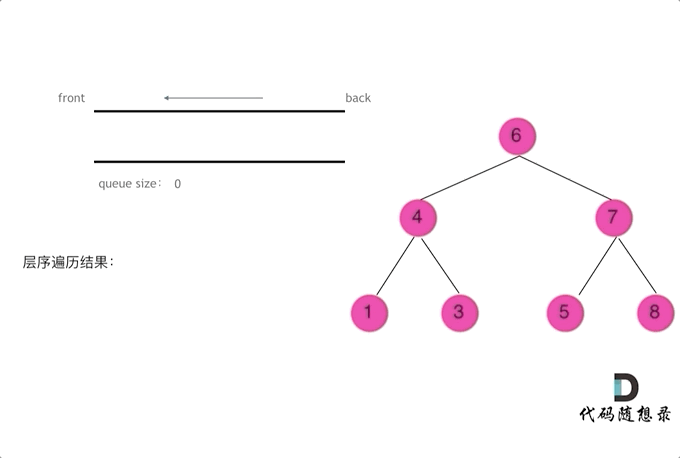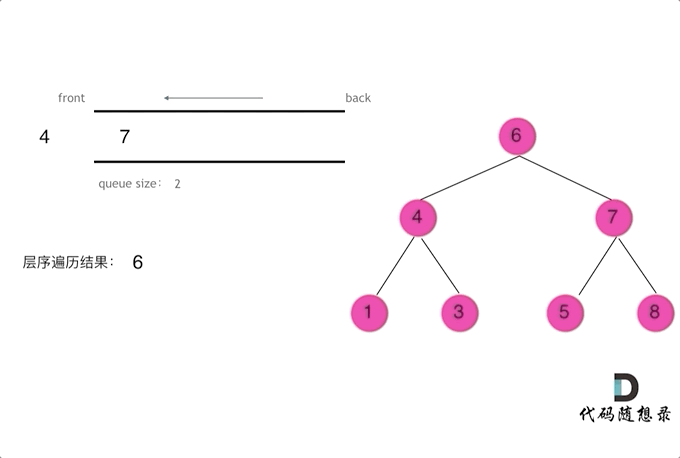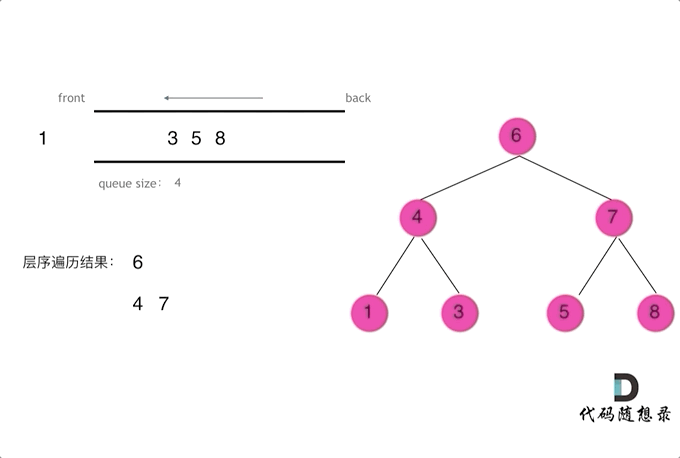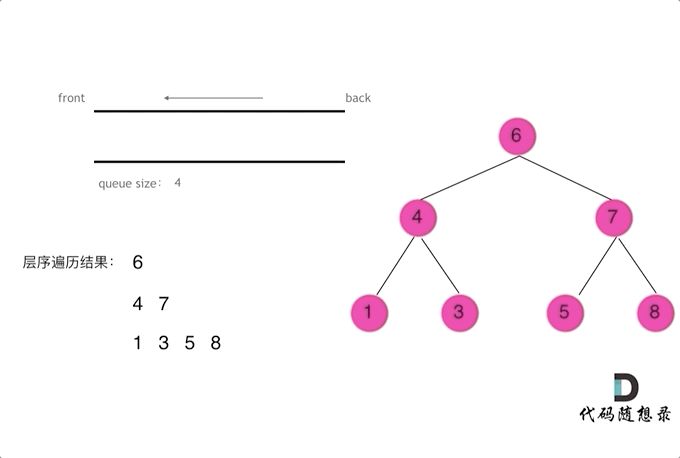
102二叉树的层序遍历

这样就实现了层序从左到右遍历二叉树。

/**
 * @description: 二叉树的层序遍历
 * @author: 刘宇浩
 * @date: 2023/1/18 14:25
 */
public class LevelOrder {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            ArrayList<Integer> list = new ArrayList<>();
            while (size-- > 0) {
                TreeNode treeNode = queue.poll();
                if (treeNode.left != null) {
                    queue.offer(treeNode.left);
                }
                if (treeNode.right != null) {
                    queue.offer(treeNode.right);
                }
                list.add(treeNode.val);
            }
            res.add(list);
        }
        return res;
    }
}

翻转二叉树

力扣题目链接(opens new window)

翻转一棵二叉树

这得怎么翻转呢？

如果要从整个树来看，翻转还真的挺复杂，整个树以中间分割线进行翻转，如图：
在这里插入图片描述

可以发现想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。

关键在于遍历顺序，前中后序应该选哪一种遍历顺序？（一些同学这道题都过了，但是不知道自己用的是什么顺序）

遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。

注意只要把每一个节点的左右孩子翻转一下，就可以达到整体翻转的效果

这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！建议拿纸画一画，就理解了

那么层序遍历可以不可以呢？依然可以的！只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的！

/**
 * @description: 翻转二叉树
 * @author: 刘宇浩
 * @date: 2023/1/18 15:24
 */
public class InvertTree {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        //前序遍历
        invertTree(root.left);
        invertTree(root.right);
        swapChildren(root);
        return root;
    }

    public void swapChildren(TreeNode root) {
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
    }
}