前言

在学习Acwing c++蓝桥杯辅导课第八讲数论-1295. X的因子链时接触到了欧拉筛法，本章就从最原始的朴素筛法来开始到最终的欧拉筛法。

本章节的测试数据n为100万，问题围绕从去找寻指定[2, n]范围找到所有质数个数开始。

当前文章已收录到博客文件目录索引：博客目录索引(持续更新)

朴素筛法（纯暴力，O(n²)）

思路：每判断一个n是否是质数，就去遍历[2, n - 1]来去看是否能够整除，若是都不能够整除表示其是一个质数。

复杂度分析：时间复杂度O(n²)

class Main {

    //朴素筛法：O(n^2^)
    public static boolean isPrime(int n) {
        for (int i = 2; i < n; i++) {
            if (n % i == 0) return false;
        }
        return true;
    }

    public static void main(String[] args) {
        long startTime = System.currentTimeMillis();
        //int N = (int) 1e6;
        int N = 100;
        int count = 0;
        for (int i = 2; i <= N; i++) {
            if (isPrime(i)) count++;
        }
        System.out.println(count);
        long endTime = System.currentTimeMillis();
        System.out.println("执行时间：" + (float) (endTime - startTime) / 1000 + "s");
    }
}

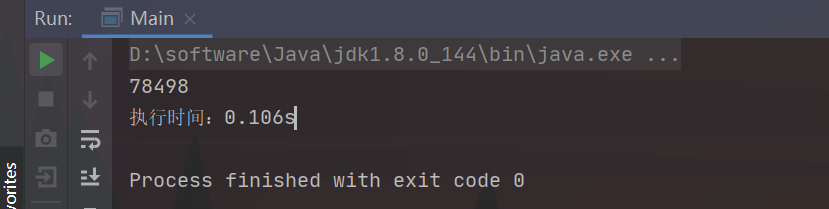
进一步来进行优化，实际上对于isPrime中遍历到的终点n实际上可以去进行开根号：

//朴素筛法优化：O(n^2^)
public static boolean isPrime(int n) {
    //开根号
    int sqt = (int) Math.sqrt(n);
    for (int i = 2; i <= sqt + 1; i++) {
        if (n % i == 0) return false;
    }
    return true;
}

其他写法：

for (int i = 2; i <= n / i; i++)
   
//不推荐，i*i可能会出现溢出情况，建议通过上面的n / i来进行不会出现溢出
for (int i = 2; i * i <= n ; i++)

埃式筛法（找出合数来确认质数, O(n*log(logn))）

合数：合数是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。

思路：首先去使用数组来存储所有的合数，接着来去判断对应的数字是否是质数。

时间复杂度：O(n*log(logn))

package com.changlu.java;

class Main {

    static int N = (int) 1e6;
    //筛选出所有的合数（为1的，合数：是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。）
    static int[] coms = new int[N + 1];

    //埃式筛法
    public static void ai(int n) {
        int sqt = (int) Math.sqrt(n);
        //这里我们来缩减范围到根号开始去找寻所有的合数
        for (int i = 2; i <= sqt + 1; i ++ ) {
            //若是当前是质数，则找出该质数的倍乘合数
            if (coms[i] == 0) {
                //最大范围应当我们要找的合数值
                for (int j = i * i; j <= n; j += i) coms[j] = 1;
            }
        }
    }

    public static void main(String[] args) {
        long startTime = System.currentTimeMillis();
        int count = 0;
        //进行埃式筛选
        ai(N);
        //判断质数
        for (int i = 2; i <= N; i++) {
            //为1的表示合数，对应0即为质数
            if (coms[i] == 0) count++;
        }
        System.out.println(count);
        long endTime = System.currentTimeMillis();
        System.out.println("执行时间：" + (float) (endTime - startTime) / 1000 + "s");
    }
}

欧拉筛法（线性筛选，O(n)）

算法思想：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。

实际上在埃式筛法中找寻合数时，对于某个数会有多次重复找到例如：

i = 2时，会找出4 7 8 16 ... n
i = 3时，则会找到6 9 12

如何来解决这种多次重复找的情况呢？此时就可以使用欧拉筛法，实际上就是埃式筛法的升级版。

在欧拉筛法中我们添加一个primes数组来记录质数，对于倍乘是针对于这个primes来围绕找新的质数的，并且一旦当前数能够整除primes数组中的值时，那么找合数环节就直接结束了！虽然说是两重循环，但是它的时间复杂度是线性的。

代码：

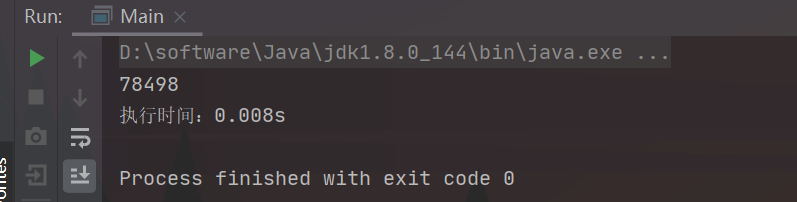
复杂度分析：时间复杂度O(n)

package com.changlu.java;

class Main {

    static int N = (int) 1e6;
    //筛选出所有的合数（为1的，合数：是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。）
    static int[] coms = new int[N + 1];
    //记录所有的质数
    static int[] primes = new int[N + 1];
    //统计质数的个数
    static int ps_pos = 0;

    //欧拉筛：可筛选出所有质数以及每个数最小的质因数
    //时间复杂度O(n)
    public static void ola(int n ) {
        //遍历所有的数情况
        for (int i = 2; i <= n; i ++ ) {
            //记录质数
            if (coms[i] == 0) primes[ps_pos++] = i;
            //依据现有的质数来去求得倍乘质数（解决埃拉筛选中重复的问题）
            //遍历质数数组primes所有项，来进行求得对应当前数i能够构成的质数
            for (int j = 0; primes[j] * i <= n && j < ps_pos; j++) {
                //设置合数
                coms[primes[j] * i] = 1;
                //如果说当前的i能够整除拥有的质数，那么直接结束（核心）
                if (i % primes[j] == 0) break;
            }
        }
    }

    public static void main(String[] args) {
        long startTime = System.currentTimeMillis();
        int count = 0;
        //进行欧拉筛选
        ola(N);
        //遍历质数的个数
        System.out.println(ps_pos);
        long endTime = System.currentTimeMillis();
        System.out.println("执行时间：" + (double) (endTime - startTime) / 1000 + "s");
    }
}