二叉树
什么是二叉树? 二叉树的基础概念? 性质? 问题?
文章目录
- 二叉树
- 一、二叉树的概念
- (一)认识二叉树
- (二)二叉树的性质
- 二、遍历二叉树
- 1.前序遍历
- 2.中序遍历
- 3.后序遍历
- 4.层序遍历
- 三丶创建二叉树
- 总结
一、二叉树的概念
(一)认识二叉树
二叉树是一种非线性的数据结构,
结点的度:一个结点含有子树的个数称为该结点的度
树的度:一棵树中,所有结点度的最大值称为树的度;
叶子结点:度为0的结点称为叶结点;
父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点;
孩子子结点:一个结点含有的子树的根结点称为该结点的子结点;
根结点:一棵树中,没有双亲结点的结点;
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
树的高度或深度:树中结点的最大层次;

满二叉树:一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的
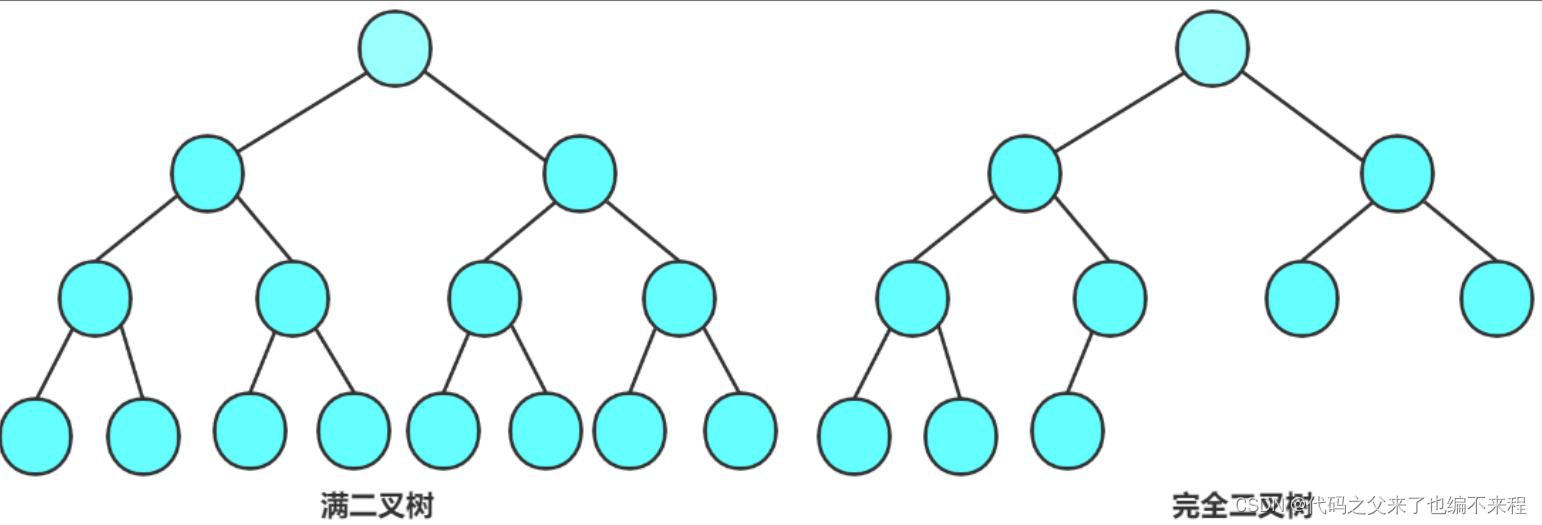
(二)二叉树的性质
1.对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
推导:

2. 具有n个结点的完全二叉树的深度k为log2(n+1)上取整
3.对于具有n个节点的完全二叉树,如果从上至下 从左到右的顺序对所有节点从0开始编号
则对于序号为i的结点有:
- 若 i > 0,双亲序号为 (i-1)/2: i 为 0 时 ,i为根结点.
- 若 2i+1<n,左孩子序号为2i + 1 否则无左孩子
- 若 2i+2<n,右孩子序号为2i + 2 否则无右孩子
二、遍历二叉树
以这颗二叉树为栗子
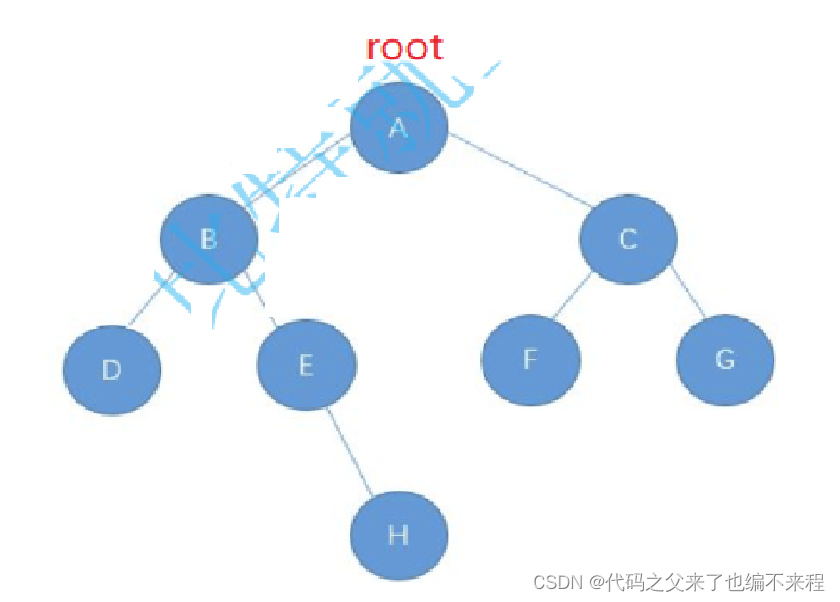
实例化节点的对象并且创建二叉树
public class binaryTree {
class TreeNode{
public char val;
private TreeNode left;
private TreeNode right;
public TreeNode(char val){
this.val = val;
}
}
public TreeNode createTree(){
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
B.left = D;
B.right = E;
E.right = H;
A.right = C;
C.left = F;
C.right = G;
return A;
}
}
遍历方式分为两种 1.递归遍历 2.非递归遍历
递归遍历:把问题拆分成子问题,判断结束条件和执行的代码
每次递归时 判断该节点是否为空 作用: 1.避免空指针异常 2.为空时就返回 执行下一步操作
1.前序遍历
递归
public void preOrder(TreeNode root){
if(root==null){
return;
}
//打印
System.out.print(root.val+" ");
//遍历左子树
preOrder(root.left);
//遍历右子树
preOrder(root.right);
}
非递归
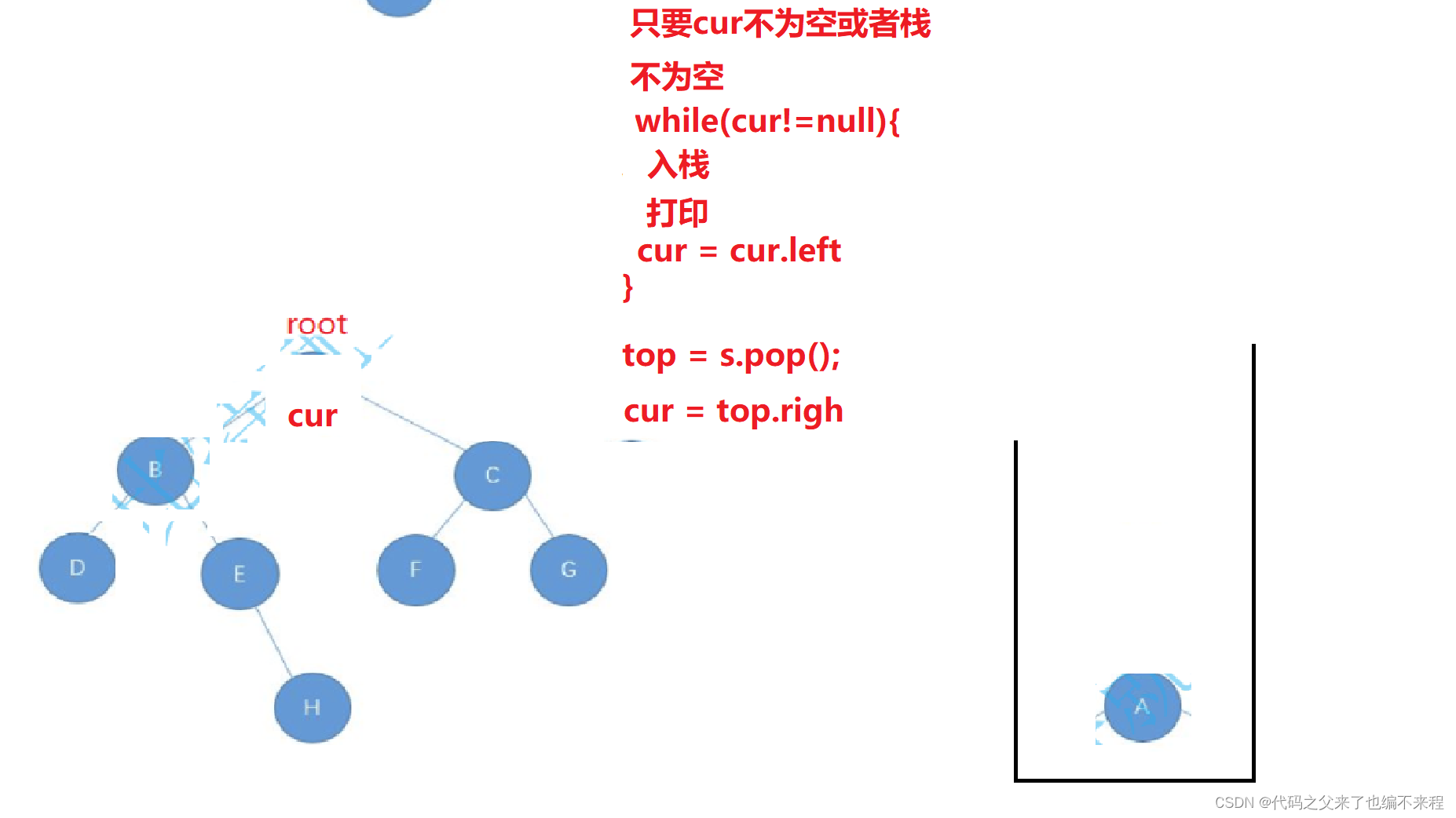
public List<Character> preOrderNot(TreeNode root){
List<Character> list = new ArrayList<>();
Stack<TreeNode> s = new Stack<>();
TreeNode cur = root;
while (cur!=null || !s.empty()) {
while(cur!=null){
s.push(cur);
list.add(cur.val);
cur = cur.left;
}
TreeNode top = s.pop();
cur = top.right;
}
return list;
}
2.中序遍历
递归
public void inOrder(TreeNode root){
if(root ==null){
return;
}
inOrder(root.left);
/*打印之前 需要把递归每一个的左子树,直到左为空
然后才能打印 , 在递归此时的右子树 不断循环
*/
System.out.print(root.val +" ");
inOrder(root.right);
}
非递归
public List<Character> inOrderNot(TreeNode root){
List<Character> list = new ArrayList<>();
Stack<TreeNode> s = new Stack<>();
TreeNode cur = root;
while (cur!=null || !s.empty()) {
while(cur!=null){
s.push(cur);
cur = cur.left;
}
TreeNode top = s.pop();
list.add(top.val);
cur = top.right;
}
return list;
}
3.后序遍历
递归
public void postOrder(TreeNode root){
if(root==null){
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val+" ");
}
非递归
public List<Character> postOrderNot(TreeNode root){
List<Character> list = new ArrayList<>();
Stack<TreeNode> s = new Stack<>();
TreeNode cur = root;
TreeNode prev = null;
while (cur!=null || !s.empty()) {
while(cur!=null){
s.push(cur);
cur = cur.left;
}
TreeNode top = s.peek();
if(top.right==null || top.right == prev){
s.pop();
list.add(top.val);
prev = top;
}else {
cur = top.right;
}
}
return list;
}
4.层序遍历
层序遍历用递归实现是不能的,因为每一层的相邻节点没有直接的关系.
所以只能用非递归,那么非递归需要如何实现呢?
此时就要借助于队列
此时来个动画演示
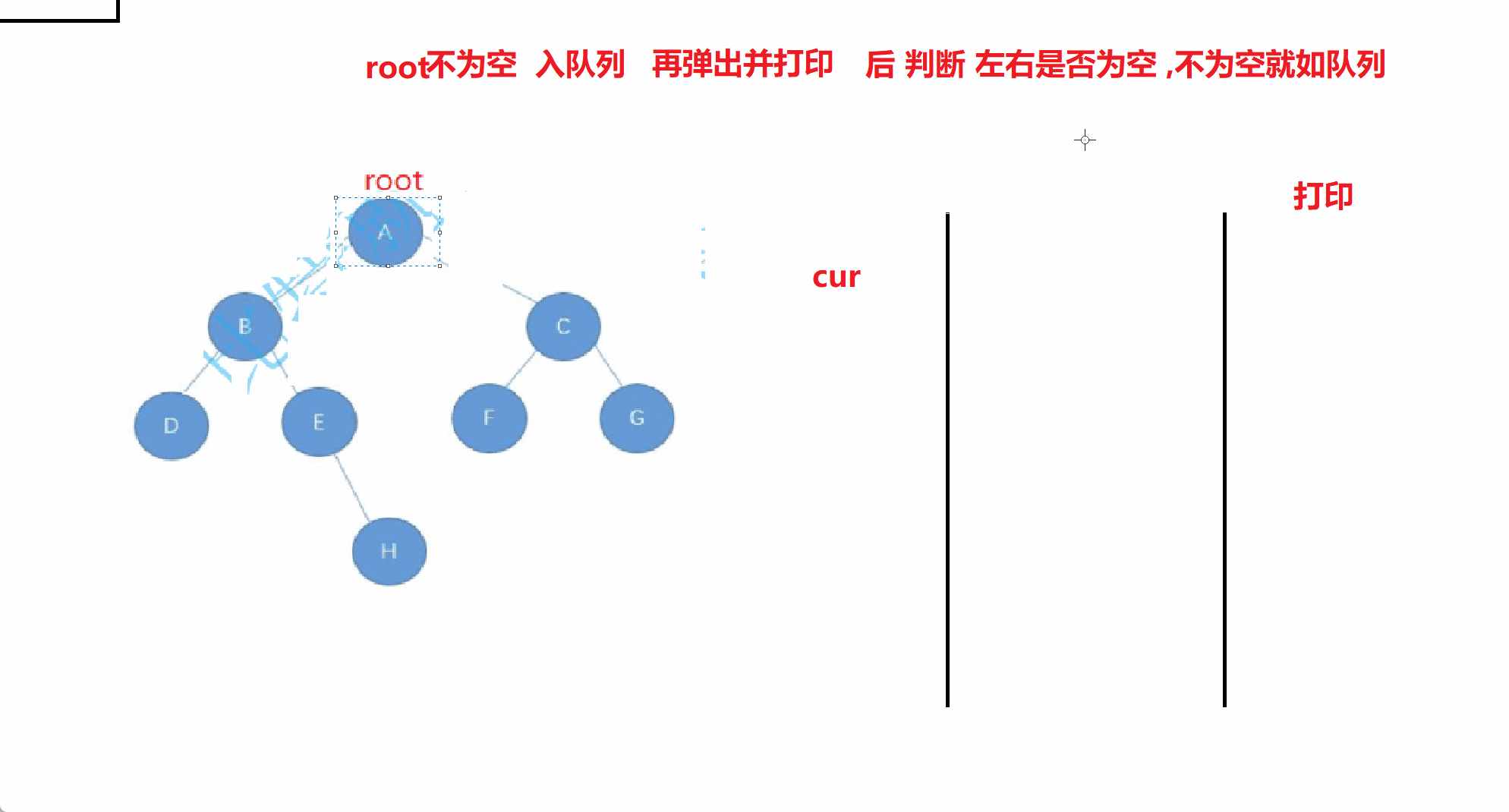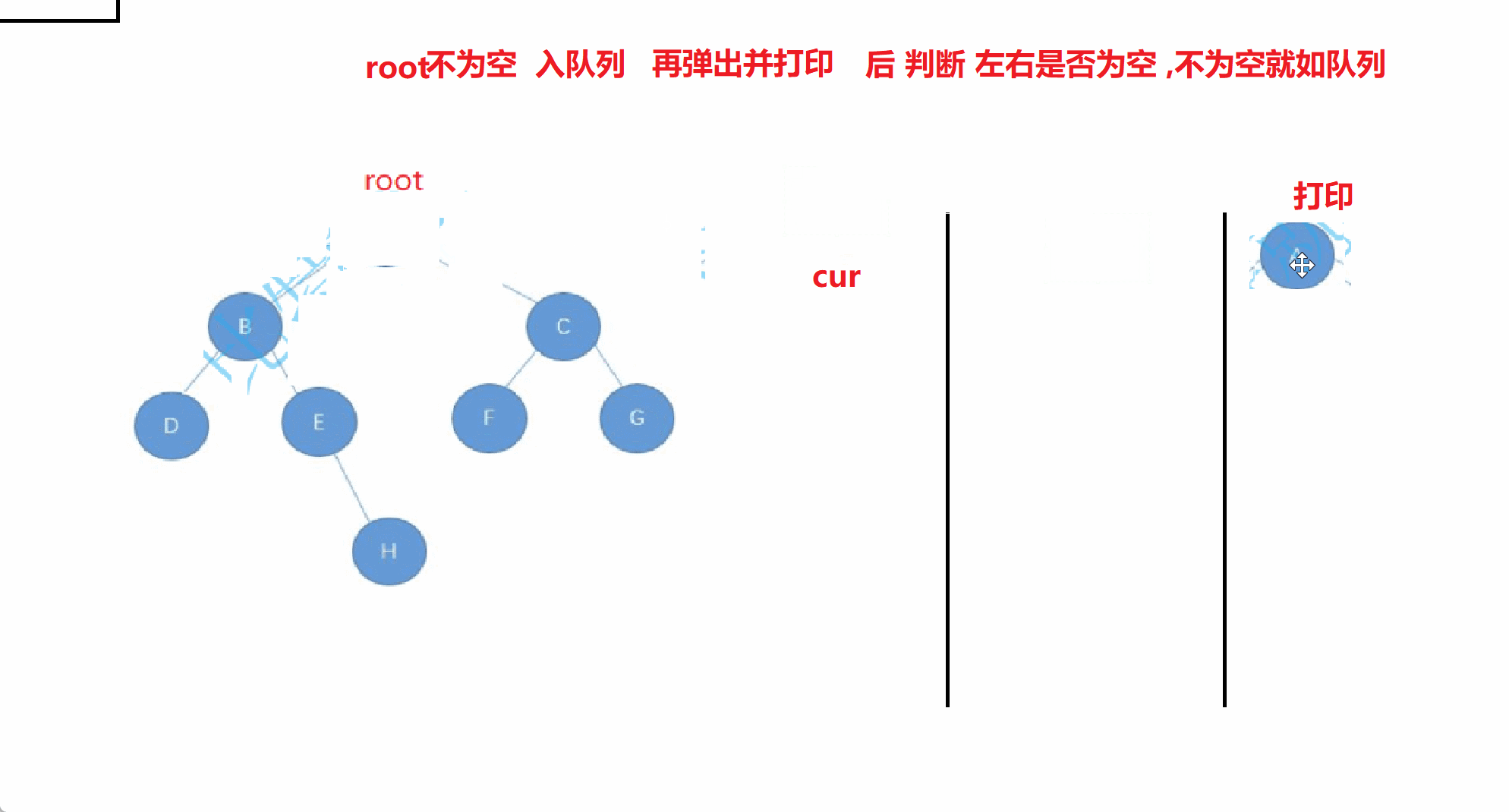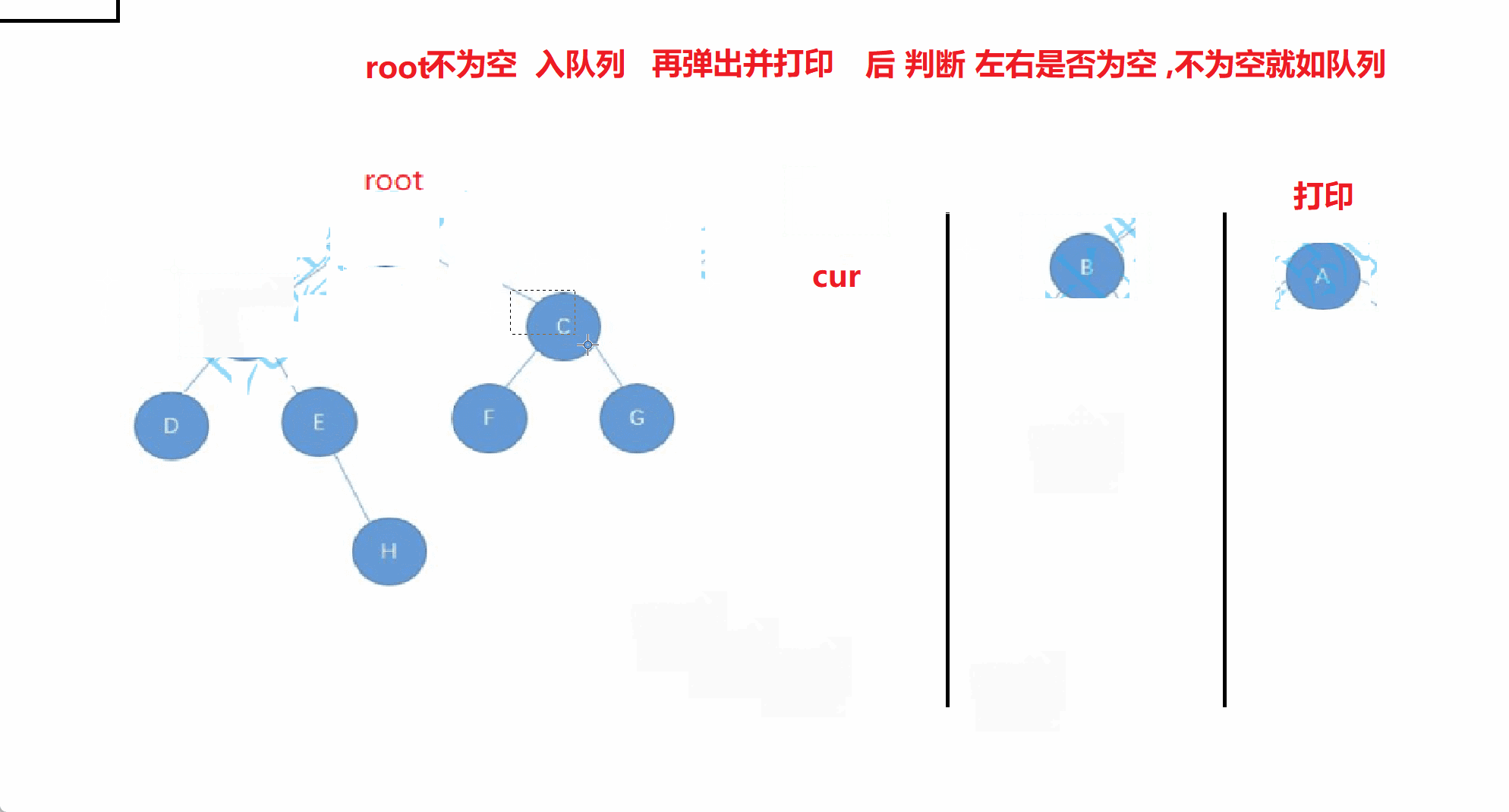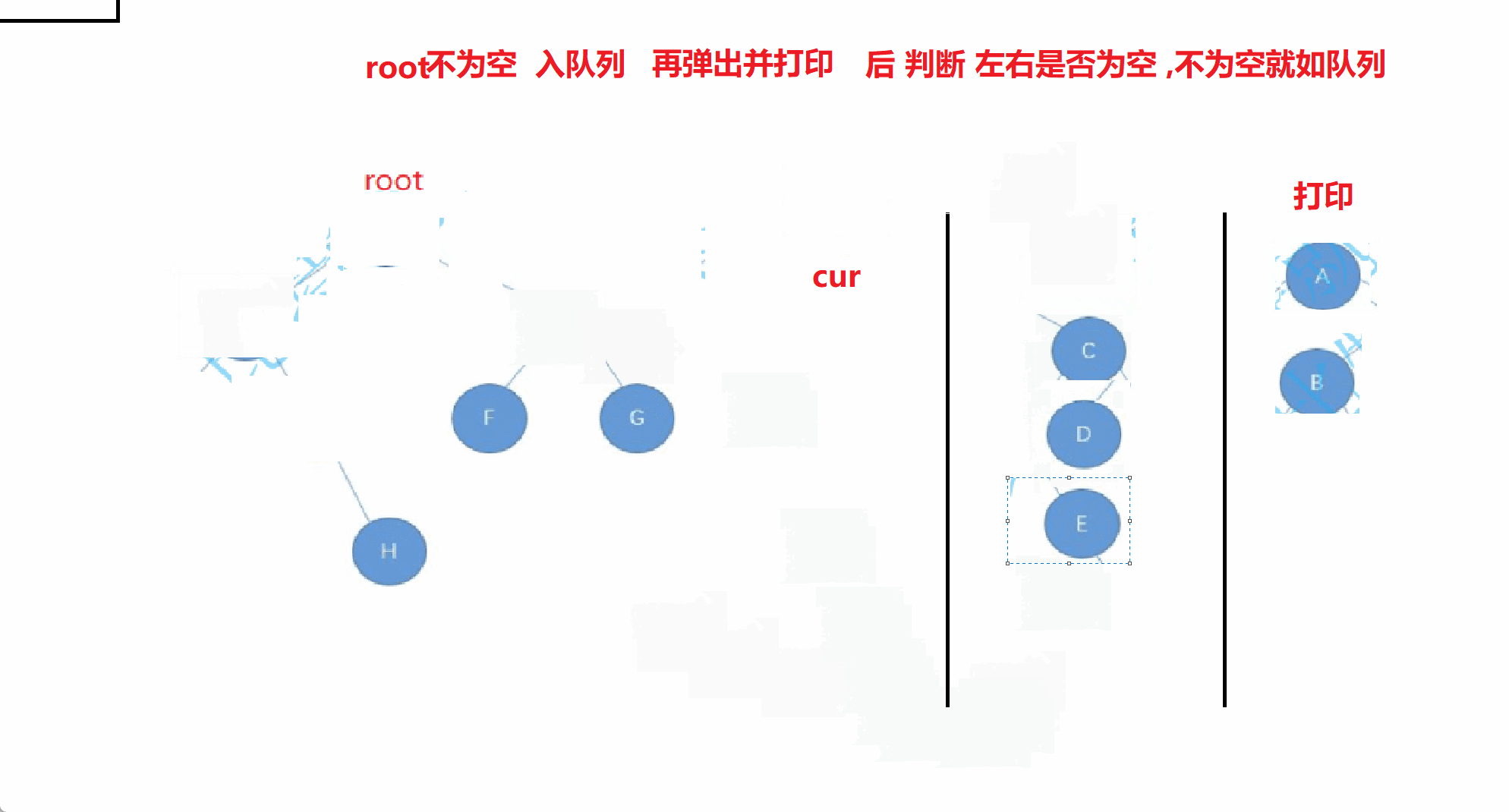
//层序遍历
public void levelOrder(TreeNode root){
if(root ==null){
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode cur = queue.poll();
System.out.print(cur.val+" ");
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
}
同时再刷下力控上的层序遍历
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<>();
if(root == null){
return ret;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while(!q.isEmpty()){
int size = q.size();
List<Integer> list = new ArrayList<>();
while(size>0){
TreeNode cur = q.poll();
list.add(cur.val);
if(cur.left!=null){
q.offer(cur.left);
}
if(cur.right!=null){
q.offer(cur.right);
}
size--;
}
ret.add(list);
}
return ret;
}
三丶创建二叉树
问题描述:编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
题目源自于二叉树遍历
import java.util.Scanner;
//new一个节点
class TreeNode{
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val){
this.val = val;
}
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
//成员变量 避免递归时出现容错
/*
根据先序字符串来创建二叉树,首先就要先遍历每一个字符,
每遍历一个不为null('#')的时候都要创建一个节点,
再不断进行i++操作 遇到字符为空时 就可以根据递归来连接每一个节点
*/
public static int i = 0;
public static TreeNode createTree(String s){
char[] ch = s.toCharArray();
TreeNode root = null;
if(ch[i]!='#'){
root = new TreeNode(ch[i]);
i++;
root.left = createTree(s);
root.right = createTree(s);
}else{
i++;
}
return root;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextLine()) { // 注意 while 处理多个 case
String s = in.nextLine();
TreeNode root = createTree(s);
inOrder(root);
}
}
//中序遍历
public static void inOrder(TreeNode root){
if(root==null){
return;
}
inOrder(root.left);
System.out.print(root.val+" ");
inOrder(root.right);
}
}
总结
提示:这里对文章进行总结:
二叉树的基础大概这些内容,这些代码一定要多理解,多敲 才能更进一步,二叉树较不易理解的内容还未更新,等下次复习的时候再更新~