目录
一、红黑树的迭代器
1.1红黑树迭代器框架
1.2operator*() && operator->()
1.3operator++()
1.4operator--()
1.5operator==() && operator!=()
1.6begin() && end()
二、如何用红黑树搭配map和set(仿函数)
三、红黑树封装map和set(简易版)
3.1红黑树的构造(RBTree.h)
3.2map的模拟实现(MyMap.h)
3.3set的模拟实现(MySet.h)
3.4测试(test.cpp)
一、红黑树的迭代器
前一篇章,有了红黑树的了解,但那只实现了红黑树的插入部分,那么现在要用红黑树封装set、map容器,那有一个功能,就必须得实现,即迭代器,对于红黑树的迭代器该如何实现呢?参考前面篇章,list容器的迭代器的实现,同样的,红黑树将迭代器要实现的功能封装成了一个类,那么接下来进行一步步实现。
1.1红黑树迭代器框架
由于迭代器的遍历,实际就是遍历节点,在实现具体步骤之前,先带上节点,再把迭代器的框架搭好。
enum Color//对于红黑节点,用枚举结构来表示
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode(const T& data, Color color = RED)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(data)
,_color(color)
{}
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Color _color;//默认给红色才符合规则,若默认给黑色的话,则插入的每个节点都是黑色节点,
//那么就不能保证每条路径的黑色节点相同,违反了第4条性质。而给红色,就可以根据规则调整。
};
template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef Node* PNode;
typedef RBTreeIterator<T, Ref, Ptr> Self;
PNode _node;
RBTreeIterator(const PNode node)
:_node(node)
{}
//.....
};1.2operator*() && operator->()
T& operator*()
{
return _node->_data;//访问节点数据
}
T* operator->()
{
return &(operator*());//operator*() == _node->_data
}1.3operator++()
对红黑树的遍历是一个中序遍历,遍历完后,得到的是一个有序序列。每++一次,跳到的位置是中序序列中的下一个位置。我们知道中序的访问顺序是,左根右,那么如何在树上进行操作而达到中序遍历呢?
大致可以分为两步:
1.当左子树与根访问完,要符合中序,得去右子树进行访问,同理右子树得满足中序遍历,首先就得找到右子树的最小节点,即最左节点。
抽象示意图:
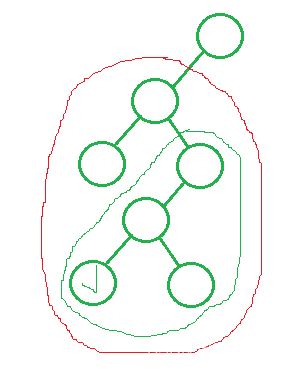
2.当左子树未访问完,++时,就指向父节点,
抽象示意图:

或者当右子树访问完了,则说明一颗节点的整个左子树访问完了。那么++就是要找到这个节点
抽象示意图:
Self& operator++()
{
if (_node->_right)//左子树访问完,去访问右子树
{
_node = _node->_right;
while (_node && _node->_left)
{
_node = _node->_left;
}
}
else//左子树未访问完,或者右子树访问完
{
PNode cur = _node;
PNode parent = cur->_parent;
while (parent && cur != parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}1.4operator--()
那么,对于--操作,它与++操作是反过来的,是从大到小的一个遍历。
1. 当右子树与根访问完,要符合大到小的遍历,得去左子树进行访问,同理左子树得满足大到小的遍历,首先就得找到左子树的最大节点,即最右节点。
2.当右子树未访问完,或者左子树已访问完
Self& operator--()
{
PNode cur = _node;
PNode parent = cur->_parent;
if (_node->_left)//右子树访问完,去左子树访问
{
_node = _node->_left;
while (_node->_right)
{
_node = _node->_right;
}
}
else//右子树未访问完,或者左子树访问完
{
PNode cur = _node;
PNode parent = cur->_parent;
if (parent && cur != parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
1.5operator==() && operator!=()
bool operator==(const Self& x) const
{
return _node == x._node;
}
bool operator!=(const Self& x) const
{
return _node != x._node;
}1.6begin() && end()
搭建好了迭代器,那么如何在红黑树中定义begin和end(),按正常的理解, begin返回指向中序序列第一个元素的迭代器,end()返回指向中序序列最后一个元素下一个位置的迭代器。
iterator begin()
{
PNode cur = _Root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}begin的返回值是没有问题,但是end就不一样了,end指向的是nullptr,当要实行end()--操作时,迭代器就会指向最后一个元素的位置,但是end已经指向空了呀,而--的操作是通过更改指针指向,那么更改end指向,就是要对空指针进行解引用,就会报错。
那么正确的做法就是将end()放在头结点的位置。即构建一个头结点用来存放begin和end,该头结点与树的头结点互相指向,对于这种做法,这里并不会去实现,还是按照原来的做法进行实现。
二、如何用红黑树搭配map和set(仿函数)
我们可以用两颗红黑树分别封装一份map和一份set,但是这样做的效果就带来了代码冗余。为了减少代码冗余,模拟跟库保持用一颗红黑树封装map和set,但是该如何做到套用一颗树呢,我们来进一步分析。
首先对于map而言,其存放的节点值是pair,而对于set存放的是key,这对于红黑树节点的实现到是没啥问题,但是对于红黑树内部的构造,是需要查询插入的位置,就需要进行比较,若将比较实现成key的比较,那么对于pair类型又该如何比较,虽然知道比较的也是pair中的key,但是如何做到既满足set中的key类型比较,又满足pair类型中的key比较,总不能干两份代码吧。这个时候,我们的仿函数又派上用场了,对于set和map中都构造一个仿函数,分别表示取到set的key,和map中pair中的key,那么红黑树中的比较,就可以换成仿函数的比较,当往set中插入元素进行比较,调用的就是set的仿函数,当往map中插入元素进行比较,调用的就是map的仿函数从而达到回调。用一张图来进行表示,如图:
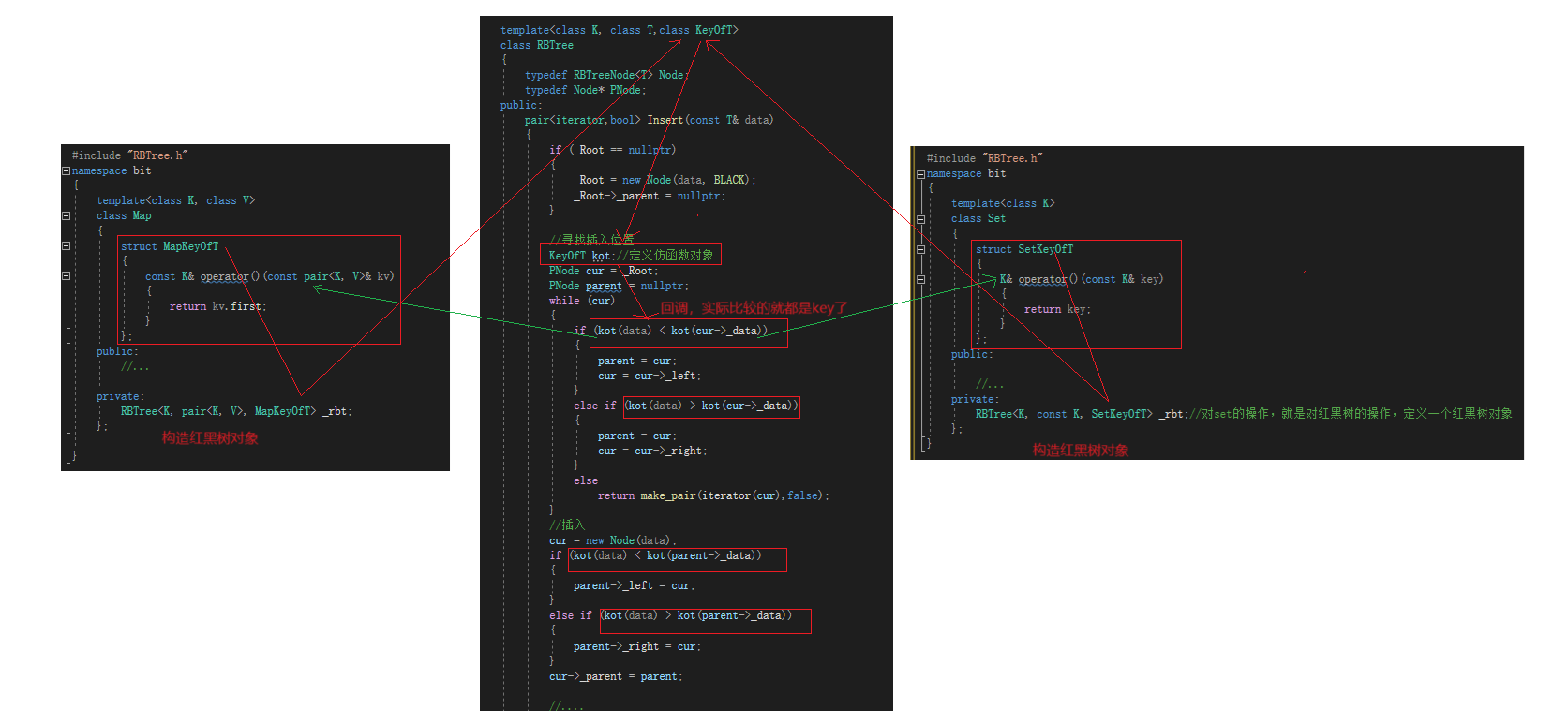
三、红黑树封装map和set(简易版)
3.1红黑树的构造(RBTree.h)
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;
namespace bit
{
enum Color//对于红黑节点,用枚举结构来表示
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode(const T& data, Color color = RED)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(data)
,_color(color)
{}
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Color _color;//默认给红色才符合规则,若默认给黑色的话,则插入的每个节点都是黑色节点,
//那么就不能保证每条路径的黑色节点相同,违反了第4条性质。而给红色,就可以根据规则调整。
};
template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef Node* PNode;
typedef RBTreeIterator<T,Ref,Ptr> Self;
PNode _node;
RBTreeIterator(const PNode node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &(operator*());
}
Self& operator++()
{
if (_node->_right)//左子树访问完,去访问右子树
{
_node = _node->_right;
while (_node && _node->_left)
{
_node = _node->_left;
}
}
else//左子树未访问完,或者右子树访问完
{
PNode cur = _node;
PNode parent = cur->_parent;
while (parent && cur != parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
PNode cur = _node;
PNode parent = cur->_parent;
if (_node->_left)//右子树访问完,去左子树访问
{
_node = _node->_left;
while (_node->_right)
{
_node = _node->_right;
}
}
else//右子树未访问完,或者左子树访问完
{
PNode cur = _node;
PNode parent = cur->_parent;
if (parent && cur != parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
bool operator==(const Self& x) const
{
return _node == x._node;
}
bool operator!=(const Self& x) const
{
return _node != x._node;
}
};
template<class K, class T,class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
typedef Node* PNode;
public:
typedef RBTreeIterator<T,T&,T*> iterator;
typedef RBTreeIterator<const T, const T&, const T*> const_iterator;
RBTree()
:_Root(nullptr)
{}
iterator begin()
{
PNode cur = _Root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
const_iterator begin() const
{
PNode cur = _Root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
const_iterator end() const
{
return iterator(nullptr);
}
pair<iterator,bool> Insert(const T& data)
{
if (_Root == nullptr)
{
_Root = new Node(data, BLACK);
_Root->_parent = nullptr;
return make_pair(iterator(_Root), true);
}
//寻找插入位置
KeyOfT kot;//定义仿函数对象
PNode cur = _Root;
PNode parent = nullptr;
while (cur)
{
if (kot(data) < kot(cur->_data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(data) > kot(cur->_data))
{
parent = cur;
cur = cur->_right;
}
else
return make_pair(iterator(cur),false);
}
//插入
cur = new Node(data);
if (kot(data) < kot(parent->_data))
{
parent->_left = cur;
}
else if (kot(data) > kot(parent->_data))
{
parent->_right = cur;
}
cur->_parent = parent;
//调整
while (parent && parent->_color == RED)//只要停留在情况一就继续判断
{
PNode grandparent = parent->_parent;
PNode uncle = nullptr;
//先定好uncle的位置,不管uncle是否存在
if (parent == grandparent->_left)
{
uncle = grandparent->_right;
}
else
{
uncle = grandparent->_left;
}
if (uncle && uncle->_color == RED)//p为红、u存在且为红
{
// g
// p u
// cur
parent->_color = BLACK;
uncle->_color = BLACK;
grandparent->_color = RED;
//根节点,更新结束
if (grandparent == _Root)
{
grandparent->_color = BLACK;
break;
}
//往上更新
cur = grandparent;
parent = cur->_parent;
}
else if (cur == parent->_left && parent == grandparent->_left )//cur为p的左孩子,p为g的左孩子,p为红
{
// g
// p u
//cur
RotateR(grandparent);
parent->_color = BLACK;
grandparent->_color = RED;
break;
}
else if (cur == parent->_right && parent == grandparent->_right )//cur为p的右孩子,p为g的右孩子,p为红
{
// g
// u p
// cur
RotateL(grandparent);
parent->_color = BLACK;
grandparent->_color = RED;
break;
}
else if (cur == parent->_right && parent == grandparent->_left )//p为g的左孩子,cur为p的右孩子,p为红
{
// g
//p u
// cur
RotateL(parent);
RotateR(grandparent);
cur->_color = BLACK;
grandparent->_color = RED;
break;
}
else if (cur == parent->_left && parent == grandparent->_right)//p为g的右孩子,cur为p的左孩子,p为红
{
// g
//u p
// cur
RotateR(parent);
RotateL(grandparent);
cur->_color = BLACK;
grandparent->_color = RED;
break;
}
else
{
assert(false);
}
}
return make_pair(iterator(cur),true);
}
iterator Find(const T& data)
{
if (_Root == nullptr)
return end();
PNode cur = _Root;
KeyOfT kot;
while (cur)
{
if (kot(data) < kot(cur->_data))
{
cur = cur->_right;
}
else if (kot(data) > kot(cur->_data))
{
cur = cur->_left;
}
else
return iterator(cur);
}
return end();
}
size_t _Size(PNode Root,int k)
{
if (Root == nullptr)
return 0;
int leftsize = _Size(Root->_left, k);
int rightsize = _Size(Root->_right, k);
return leftsize + rightsize + 1;
}
size_t Size()
{
int k = 0;
return _Size(_Root, k);
}
bool Empty()
{
return _Root == nullptr;
}
void RotateL(PNode parent)
{
PNode subR = parent->_right;
PNode subRL = subR->_left;
PNode pparent = parent->_parent;
if (parent == _Root)//更新根节点
{
_Root = subR;
subR->_parent = nullptr;
}
else
{
//更新parent的父节点指向
if (parent == pparent->_left)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;
}
subR->_parent = pparent;
}
//parent的右指针指向subRL,subRL的父节点指向parent
parent->_right = subR->_left;
if (subRL)//subR的左节点可能不存在
subRL->_parent = parent;
//subR的左指针指向parent,parent的父节点指向subR
subR->_left = parent;
parent->_parent = subR;
}
//右单旋
void RotateR(PNode parent)
{
PNode subL = parent->_left;
PNode subLR = subL->_right;
PNode pparent = parent->_parent;
if (_Root == parent)
{
_Root = subL;
subL->_parent = nullptr;
}
else
{
//更新parent的父节点指向
if (pparent->_left == parent)
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
subL->_parent = pparent;
}
//parent的左指针指向subLR,subLR的父节点指向parent
parent->_left = subLR;
if (subLR)//subR的右节点可能不存在
subLR->_parent = parent;
//subL的右指针指向parent,parent的父节点指向subL
subL->_right = parent;
parent->_parent = subL;
}
private:
PNode _Root;
};
}3.2map的模拟实现(MyMap.h)
#pragma once
#include "RBTree.h"
namespace bit
{
template<class K,class V>
class Map
{
struct MapKeyOfT
{
const K& operator()(const pair<K,V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::const_iterator const_iterator;
iterator begin()
{
return _rbt.begin();
}
iterator end()
{
return _rbt.end();
}
const_iterator begin() const
{
return _rbt.begin();
}
const_iterator end() const
{
return _rbt.end();
}
pair<iterator,bool> insert(const pair<K,V>& kv)
{
return _rbt.Insert(kv);
}
V& operator[](const K& data)
{
pair<iterator, bool> p = _rbt.Insert(make_pair(data, V()));//插入失败,说明data已经存在,返回指向data的迭代器
return p.first->second;
}
iterator find(const K& data)
{
return _rbt.Find(data);
}
size_t size()
{
return _rbt.Size();
}
bool empty()
{
return _rbt.Empty();
}
private:
RBTree<K, pair<K,V>, MapKeyOfT> _rbt;
};
}
3.3set的模拟实现(MySet.h)
#pragma once
#include "RBTree.h"
namespace bit
{
template<class K>
class Set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;//set的迭代器使用的就是红黑树的迭代器
typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;//set的迭代器使用的就是红黑树的迭代器
iterator begin()//获取set的首元素位置的迭代器,即获取红黑树的最小元素的迭代器
{
return _rbt.begin();
}
iterator end()
{
return _rbt.end();
}
const_iterator begin() const
{
return _rbt.begin();
}
const_iterator end() const
{
return _rbt.end();
}
pair<iterator,bool> insert(const K& key)//插入元素实际就是插入到红黑树节点中去
{
return _rbt.Insert(key);
}
iterator find(const K& data)
{
return _rbt.Find(data);
}
size_t size()
{
return _rbt.Size();
}
bool empty()
{
return _rbt.Empty();
}
private:
RBTree<K,const K,SetKeyOfT> _rbt;//对set的操作,就是对红黑树的操作,定义一个红黑树对象
};
}
3.4测试(test.cpp)
#define _CRT_SECURE_NO_WARNINGS 1
#pragma warning(disable:6031)
#include "MyMap.h"
#include "MySet.h"
void TestMapRBTree()
{
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
bit::Map<int, int> t;
for (auto e : a)
{
t.insert(make_pair(e, e));
}
bit::Map<int, int>::iterator it = t.begin();
while (it != t.end())
{
cout << it->first << ":" << it->second << endl;
++it;
}
cout << endl;
}
void TestSetRBTree()
{
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
bit::Set<int> t;
for (auto e : a)
{
t.insert(e);
}
bit::Set<int>::iterator it = t.begin();
while (it != t.end())
{
cout << *it << endl;
++it;
}
cout << t.size() << endl;
cout << boolalpha << t.empty() << endl;
}
int main()
{
TestMapRBTree();
TestSetRBTree();
return 0;
}输出结果:

以上实现的是一个红黑树简易版,虽然功能并不齐全,但目标是为了进一步学习对红黑树、map和set的掌握理解。end~