目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2024年,C Yuan受到青蒿素药物治疗疟疾过程启发,提出了青蒿素优化算法(Artemisinin Optimization, AO)。


2.算法原理
2.1算法思想
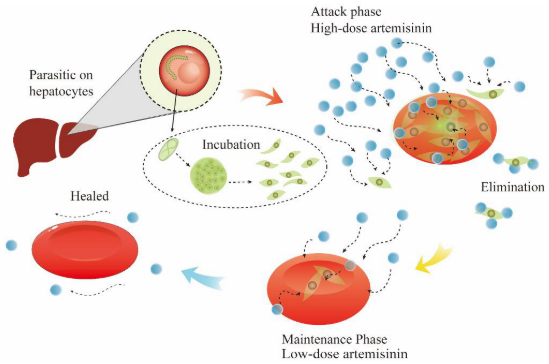
AO灵感来自于疟疾的青蒿素药物治疗过程,该过程涉及全面根除人体内的疟疾寄生虫。AO包括三个优化阶段:模拟全局探索的全面消除阶段,局部开发的局部清除阶段,以及增强算法逃避局部最优能力的后巩固阶段。
2.2算法过程
全面消除阶段
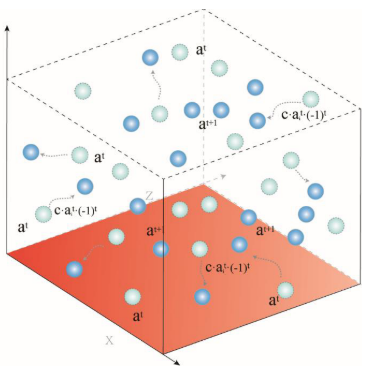
在疟疾治疗的初始阶段,给病人更大剂量的药物,以迅速控制疾病的进展。青蒿素一旦被吸收,就会随着血液被输送到人体的各个部位而扩散到全身。药物扩散过程:
{
a
i
,
j
t
+
1
=
a
i
,
j
t
+
c
×
a
i
,
j
t
×
(
−
1
)
t
,
r
a
n
d
<
0.5
a
i
,
j
t
+
1
=
a
i
,
j
t
+
c
×
b
e
s
t
j
t
×
(
−
1
)
t
,
r
a
n
d
>
0.5
(1)
\left.\left\{\begin{matrix}\mathrm{a_{i,j}^{t+1}=a_{i,j}^{t}+c\times a_{i,j}^{t}\times(-1)^{t},rand<0.5}\\\mathrm{a_{i,j}^{t+1}=a_{i,j}^{t}+c\times best_{j}^{t}\times(-1)^{t},rand>0.5}\end{matrix}\right.\right.\tag{1}
{ai,jt+1=ai,jt+c×ai,jt×(−1)t,rand<0.5ai,jt+1=ai,jt+c×bestjt×(−1)t,rand>0.5(1)
青蒿素类药物在人体内的扩散遵循药代动力学原理,考虑到药物浓度会随着时间的推移而降低,c表示药物浓度在人体内的衰减指数,青蒿素药物浓度的衰减可以用单室模型描述:
d
C
d
t
=
−
k
×
C
C
(
t
)
=
C
0
×
e
(
−
k
×
t
)
(2)
\frac{dC}{dt}=-k\times C\\C(t)=C_{0}\times e^{(-k\times t)}\tag{2}
dtdC=−k×CC(t)=C0×e(−k×t)(2)
因此,青蒿素药物浓度的指数c表述为:
c
=
1
×
e
−
(
4
×
f
M
a
x
f
)
(3)
c=1\times e^{-(4\times\frac f{Maxf})}\tag{3}
c=1×e−(4×Maxff)(3)
概率系数K表述为:
K
=
1
−
f
1
/
6
M
a
x
f
1
/
6
(4)
K=1-\frac{f^{1/6}}{Maxf^{1/6}}\tag{4}
K=1−Maxf1/6f1/6(4)
综合淘汰阶段策略:
{
a
i
,
j
t
+
1
=
a
i
,
j
t
+
c
×
a
i
,
j
t
×
(
−
1
)
t
,
r
a
n
d
<
0.5
a
i
,
j
t
+
1
=
a
i
,
j
t
+
c
×
b
e
s
t
j
t
×
(
−
1
)
t
,
r
a
n
d
>
0.5
,
r
1
<
K
(5)
\left.\left\{\begin{matrix}a_{i,j}^{t+1}=a_{i,j}^{t}+c\times a_{i,j}^{t}\times(-1)^{t},\mathrm{rand}<0.5\\a_{i,j}^{t+1}=a_{i,j}^{t}+c\times best_{j}^{t}\times(-1)^{t},rand>0.5\end{matrix}\right.,r_{1}<K\right.\tag{5}
{ai,jt+1=ai,jt+c×ai,jt×(−1)t,rand<0.5ai,jt+1=ai,jt+c×bestjt×(−1)t,rand>0.5,r1<K(5)
在最初的治疗阶段之后,随着疾病得到控制,治疗过渡到维持阶段,以确保彻底治愈疟疾。
局部清除阶段
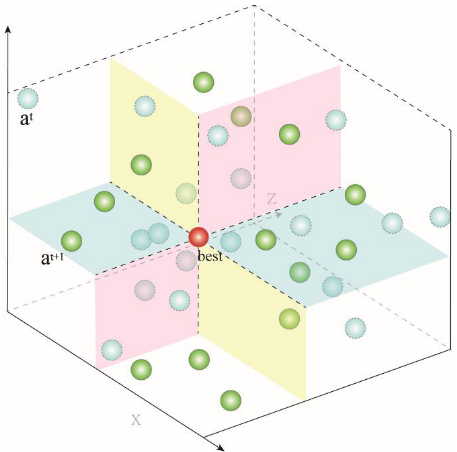
局部清除阶段的目标是消除体内任何残留的疟疾寄生虫,防止其繁殖和疟疾症状的复发。在这一阶段,患者继续接受低剂量青蒿素及其衍生物的治疗,以确保完全根除疟疾寄生虫,尽量减少在人体内发生不良反应的风险。局部清除阶段策略:
a
i
t
+
1
=
a
b
3
t
+
d
×
(
a
b
1
t
−
a
b
2
t
)
,
i
f
r
a
n
d
<
F
i
t
n
o
r
m
(
i
)
F
i
t
n
o
r
m
(
i
)
=
f
i
t
(
i
)
−
min
(
f
i
t
)
max
(
f
i
t
)
−
min
(
f
i
t
)
b
1
,
b
2
,
b
3
∼
U
(
1
,
N
)
,
b
1
≠
b
2
≠
b
3
(6)
a_{i}^{t+1}=a_{b_{3}}^{t}+d\times\left(a_{b_{1}}^{t}-a_{b_{2}}^{t}\right),if rand<Fit_{norm}(i)\\Fit_{norm}(i)=\frac{fit(i)-\min{(fit)}}{\max(fit)-\min{(fit)}}\\b_{1},b_{2},b_{3}\sim U(1,N),b_{1}\neq b_{2}\neq b_{3}\tag{6}
ait+1=ab3t+d×(ab1t−ab2t),ifrand<Fitnorm(i)Fitnorm(i)=max(fit)−min(fit)fit(i)−min(fit)b1,b2,b3∼U(1,N),b1=b2=b3(6)
后巩固阶段
对疾病的严重程度漠不关心和治疗期间的松懈是危险的有害因素,在这种策略中,假设不活跃的寄生虫形式仍然存在于人体内。不幸的是,尽管这些休眠寄生虫持续存在,一些患者仍可能再次出现疟疾。该策略表述为:
{
a
i
,
j
t
+
1
=
a
i
,
j
t
,
i
f
r
a
n
d
<
0.05
a
i
,
j
t
+
1
=
b
e
s
t
i
,
j
,
i
f
r
a
n
d
<
0.2
(7)
\left\{\begin{matrix}a_{i,j}^{t+1}=a_{i,j}^{t},if rand<0.05\\a_{i,j}^{t+1}=best_{i,j},if rand<0.2\end{matrix}\right.\tag{7}
{ai,jt+1=ai,jt,ifrand<0.05ai,jt+1=besti,j,ifrand<0.2(7)
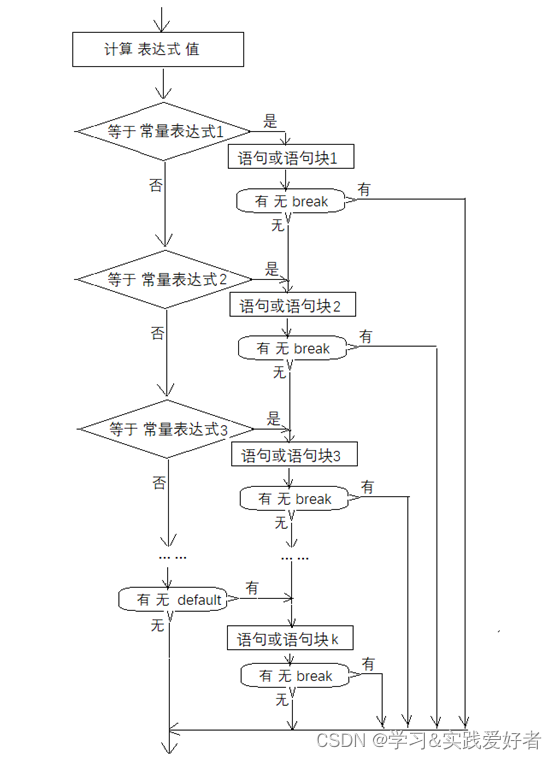
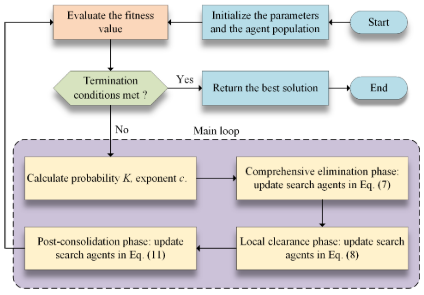
流程图
伪代码

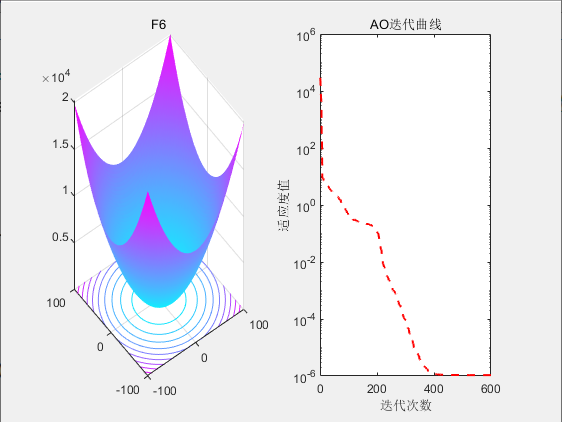
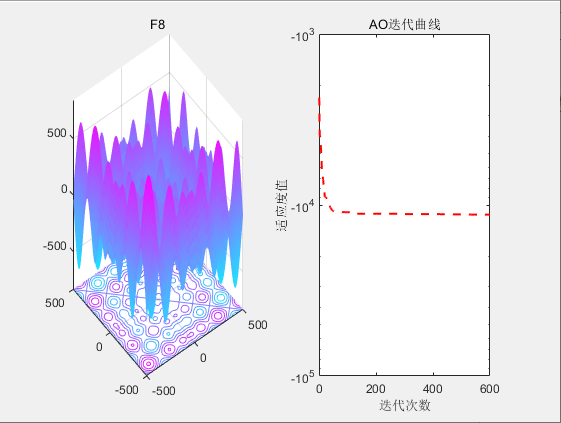
3.结果展示
4.参考文献
[1] Yuan C, Zhao D, Heidari A A, et al. Artemisinin optimization based on malaria therapy: Algorithm and applications to medical image segmentation[J]. Displays, 2024: 102740.
5.代码获取
资源清单