目录
- 1.算法原理
- 2.二维路径规划数学模型
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
【智能算法】北方苍鹰优化算法(NGO)原理及实现
2.二维路径规划数学模型
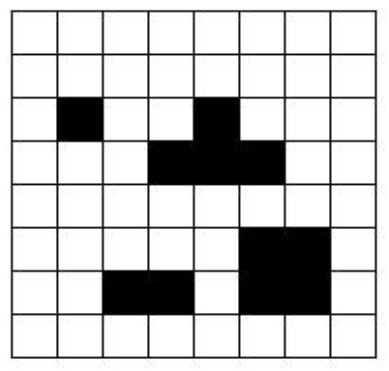
栅格法模型最早由 W.E. Howden 于 1968 年提出,障碍物的栅格用黑色表示,可通过的自由栅格用白色表示。
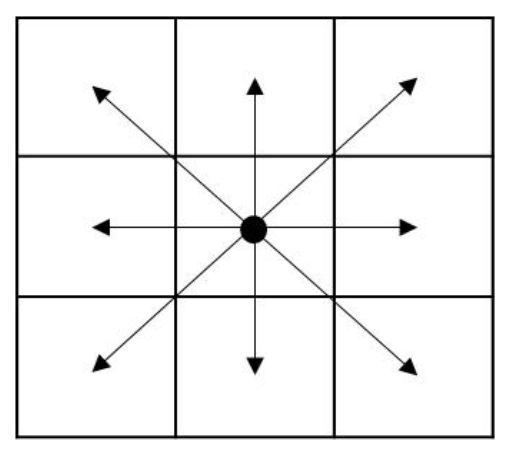
求解二维路径规划问题时,一般采用八领域搜索。
优化目标
路径规划问题需要考虑三点:
- 全局总路径最优
- 避免碰撞到障碍物
- 路径平滑性
全局总路径最优
考虑路径规划问题的全局最优路径长度最短,适应度函数可以定义为:
F
1
=
∑
i
=
0
m
−
1
(
x
i
+
1
−
x
i
)
2
+
(
y
i
+
1
−
y
i
)
2
(1)
F_1 = \sum_{i = 0}^{m-1}\sqrt{\left( x_{i+1} - x_i \right)^2 + \left( y_{i+1} - y_i \right)^2}\tag{1}
F1=i=0∑m−1(xi+1−xi)2+(yi+1−yi)2(1)
避免碰撞到障碍物
通常考虑添加惩罚函数,当下一步路径将与障碍物发生碰撞时,对其进行惩罚:
F
2
=
ϕ
⋅
Q
(2)
F_2=\phi\cdot Q\tag{2}
F2=ϕ⋅Q(2)
路径平滑性
通常采用方法包括B样条曲线、贝塞尔曲线、最小路径曲率等。
3.结果展示
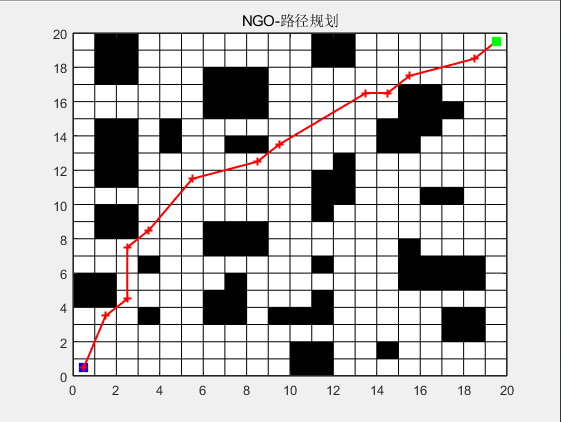
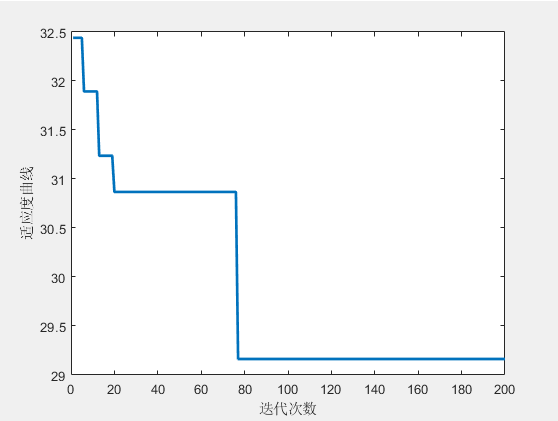
4.参考文献
[1] 梁景润,刘丽桑,陈炯晖,等.多策略优化麻雀搜索算法及其路径规划的应用[J].福建理工大学学报,2023,21(06):605-612.
[2] 邓明杰.面向路径规划的群智能优化算法研究[D].江西理工大学,2023.
[3] 张恩浩.基于麻雀搜索算法的移动机器人路径规划算法研究[D].重庆理工大学,2022.
5.代码获取
资源清单