第二章.线性回归以及非线性回归
2.12 岭回归(Ridge Regression)
1.前期导入:
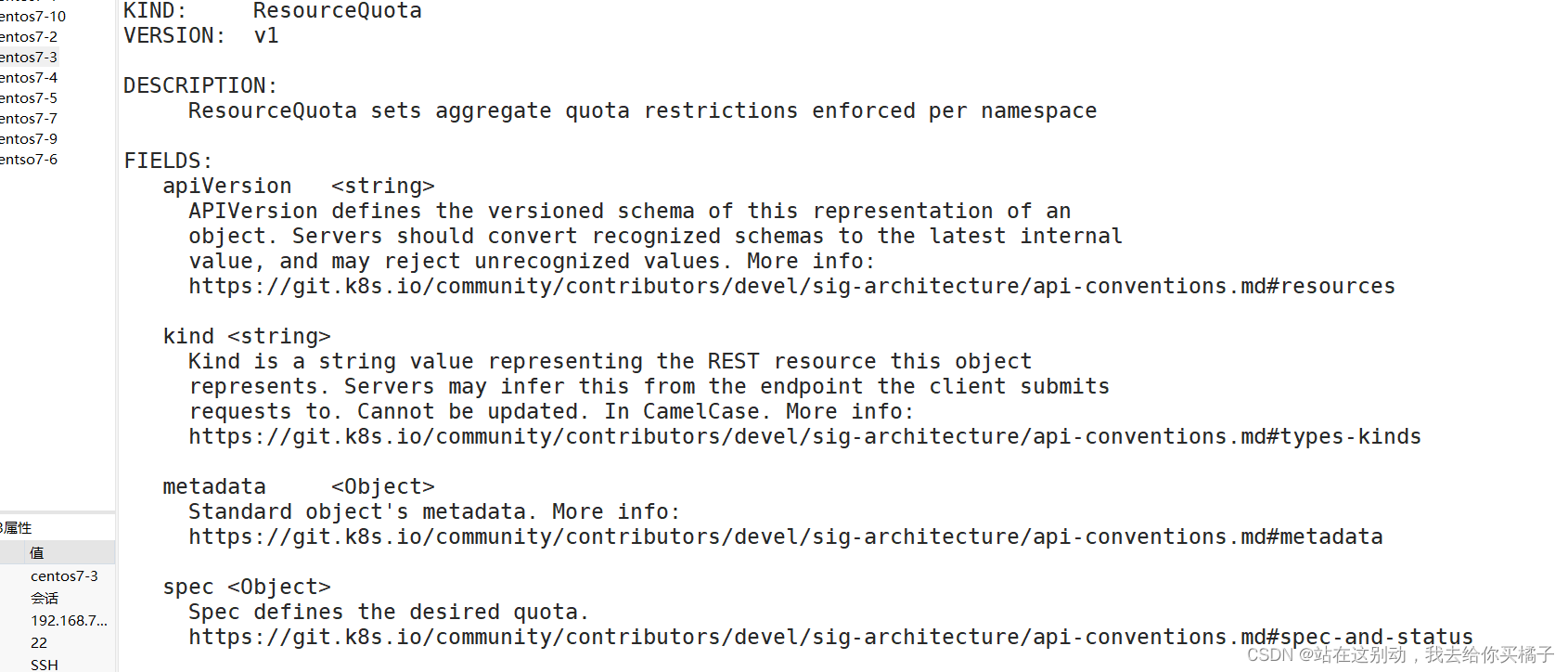
1).标准方程法[w=(XTX)-1XTy]存在的缺陷:
- 如果数据的特征比样本点还多,数据特征n,样本个数m,如如果n>m,则计算 (XTX)-1 时会出错,因为 (XTX) 不是满秩,所以不可逆
2).解决标准方程法缺陷的方法:
- 为了解决这个问题,统计学家们引入了岭回归的概念:w=(XTX+λI)-1XTy
- 参数说明:
λ:岭系数
I:单位矩阵(对角线上全为1,其他元素都为0)
2.矩阵公式:
1).矩阵转置公式
| 公式 |
|---|
| (mA)T = mAT |
| (A+B)T = AT+ BT |
| (AB)T = BTAT |
| (AT)T = A |
2).矩阵求导公式
对X求偏导
| 公式 |
|---|
| (XT) ’ = I |
| (AXT) ’ = A |
| (XTA) ’ = A |
| (AX) ’ = AT |
| (XA) ’ = AT |
| (XTAX) ’ = (A +AT)X |
| (XTAX) ’ =2AX(A为对称矩阵) |
3.岭回归公式分析:
1).L2正则化的代价函数:
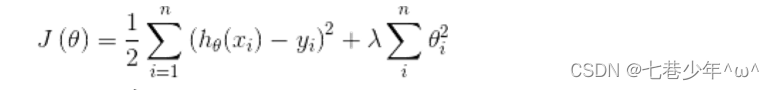
2).L2正则化用矩阵表示:
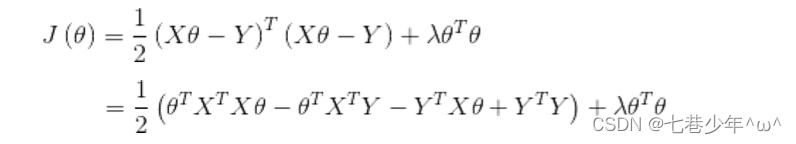
3).对θ求偏导:
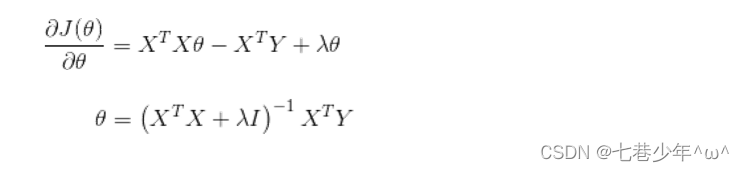
注:λI = λ
4.岭回归模型的使用场景:
1).定义:
- 岭回归最早是用来处理特征数多于样本的情况,现在也用于在估计中加入偏差,从而得到更好的估计,同时也可以解决多重共线性的问题,岭回归是一种偏估计。
2).岭回归代价函数:
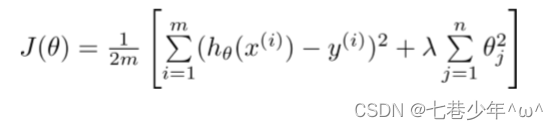
3).岭回归求解:
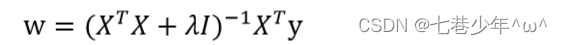
- 参数说明:
λ:岭系数
I:单位矩阵(对角线上全为1,其他元素都为0)
4).λ值选取的方法:
- 各回归系数的岭估计基本稳定
- 残差平方和增加不太多
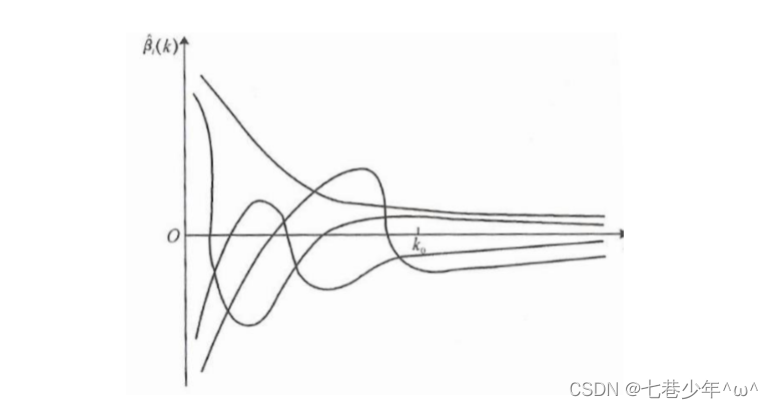
- 图像的描述:y轴:每条线代表一个参数的变化,x轴:代表λ的参数值,λ越大,参数越接近于0
4.longley数据集的介绍:
- longley数据集是强共线性的宏观经济数据,包含GNP deflator(GNP 平减指数)、GNP(国民生产总值)、Unemployed(失业率)、ArmedForces(武装力 量)、Population(人口)、year(年份),Emlpoyed(就业率)。
- Longley数据集存在严重的多重共线性问题,在早期经常用来检验各种算法或者计算集的计算精度。
5.实战1: 标准方程法—岭回归:
1).CSV中的数据:
- longley.csv
2).代码
import numpy as np
from numpy import genfromtxt
# 读取数据
data = genfromtxt('D:\\Data\\longley.csv', delimiter=',')
# 数据切片
x_data = data[1:, 2:]
y_data = data[1:, 1, np.newaxis]
# 给样本增加偏置项
X_data = np.concatenate((np.ones((16, 1)), x_data), axis=1)
# 岭回归标准方程法求解回归参数
def weights(xArr, yArr, lam=0.2):
xMat = np.mat(xArr)
yMat = np.mat(yArr)
# 矩阵乘法
xTx = xMat.T * xMat
rxTx = xTx + lam * np.eye(xMat.shape[1])
# 判断矩阵是否为可逆矩阵
if np.linalg.det(rxTx) == 0.0:
print('This matrix cannot do inverse')
return
ws = rxTx.I * xMat.T * yMat
return ws
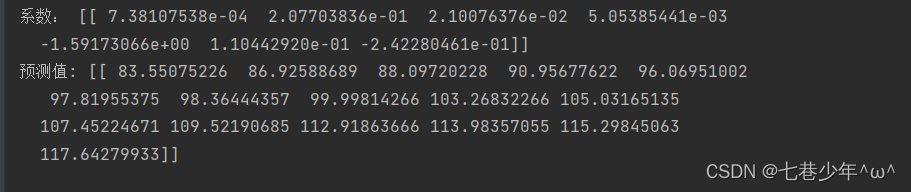
ws = weights(X_data, y_data)
print('系数:', ws.reshape(1, ws.shape[0]))
# 预测值
pred = np.mat(X_data) * np.mat(ws)
print('预测值:', pred.reshape(1, pred.shape[0]))
3).结果展示:
①.数据
5.实战2: sklearn—岭回归:
1).CSV中的数据:
- longley.csv
2).代码
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from sklearn import linear_model
# 导入数据
data = genfromtxt('D:\\Data\\longley.csv', delimiter=',')
# 数据切片
x_data = data[1:, 2:]
y_data = data[1:, 1]
# 生成50个值:岭回归的备选值
alphas_to_test = np.linspace(0.001, 1, 50)
# 创建模型:alphas:岭回归系数 store_cv_values:岭回归的误差值
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True)
# 拟合线性模型
model.fit(x_data, y_data)
# 岭系数
coeff = model.alpha_
print('岭系数:', coeff)
# Loss值
loss = model.cv_values_.shape
print('Loss值的形状:', loss)
pred = model.predict(x_data[:])
print('预测值:', pred)
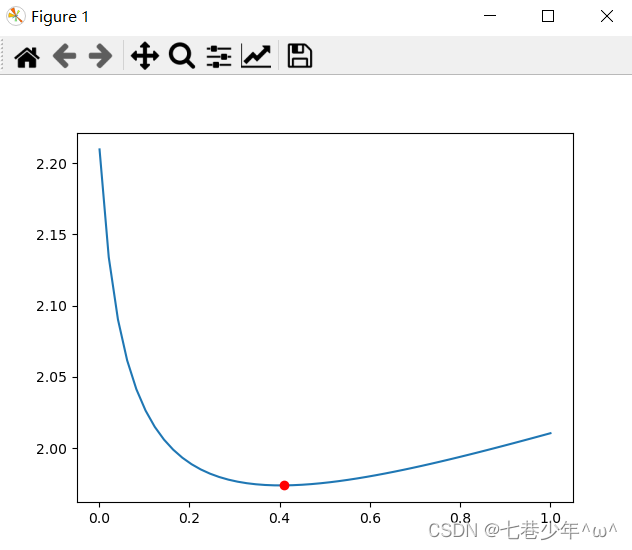
# 画图:岭系数跟loss的关系
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
# 选取的岭系数值的位置
plt.plot(coeff, min(model.cv_values_.mean(axis=0)), 'ro')
plt.show()
3).结果展示:
①.数据
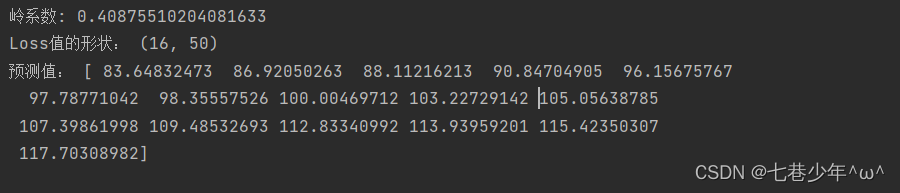
②.图像