第三次作业【动态规划】

文章目录
- 第三次作业【动态规划】
- <1>算法实现题 3-1 独立任务最优解问题
- <2>算法实现题 3-4 数字三角形问题
- <3>算法实现题 3-8 最小m段和问题
- <4>算法实现题 3-25 m处理器问题
<1>算法实现题 3-1 独立任务最优解问题
▲问题重述
用两台处理机A 和 B处理n 个作业。设第个作业交给机器A处理时需要时间ai,若由机器 B 来处理,则需要时间 b。由于各作业的特点和机器的性能关系,可能对于某些,有azb,而对于某些jjfi),有ab。既不能将一个作业分开由两台机器处理也没有一台机器能同时处理2个作业。设计一个动态规划算法,使得这两台机器处理完这n
个作业的时间最短(从任何一台机器开工到最后一台机器停工的总时间)。研究一个实例:(a1,a2,a3,a4,as,a6)=(2,5,7,10,5,2),(b, b2,b, b4, bs, b6)=(3,8,4,11,3,4)。
算法设计:对于给定的两台处理机A 和 B 处理个作业,找出一个最优调度方案,使2
台机器处理完这n个作业的时间最短。
数据输入:由文件 inputtxt 提供输入数据。文件的第1行是1个正整数n,表示要处理
n个作业。在接下来的2行中,每行有n个正整数,分别表示处理机A和B 处理第i个作业需要的处理时间。
案例:
input.txt
6
2 5 7 10 5 2
3 8 4 11 3 4
output.txt
15
▲解题思路
状态转移方程:dp[i][j]=min(dp[i-1][j]+b[i],dp[i-1][j-a[i]]);
dp[i][j]代表做完前i个任务,A机器花几分钟情况下,B机器所花的时间,也就是说dp[i][j]就是表示B机器所花时间。
dp[i][j] = dp[i-1][j]+b[i]代表第i个任务交给B来做,所以做完前i个任务的时候,A机器和前i - 1的任务一样,还是花了j分钟,而B机器则花dp[i-1][j]+b[i]分钟;
dp[i][j] = dp[i-1][j-a[i]]代表第i个任务交给A来做,现在的A机器花费时间是j,所以在前i - 1个任务完成的时候,A机器是花了j-a[i]分钟的,所以现在B机器还是花了dp[i-1][j-a[i]]分钟;
一直到dp[n][i]:代表所有的任务都做完了,B机器所花费的时间,那么最迟的时间就是B的时间和A的时间求最大值;
最后这个循环for(int i=0; i<=sum; i++)ans=min(ans,max(dp[n][i],i));//max(dp[n][i],i) 表示完成前n个作业A机器花i分钟 B机器花dp[n][i]分钟情况下,最迟完工时间
▲代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 100;
const double eps = 1e-6;
int Data[MAXN];
int a[MAXN], b[MAXN];
int dp[500][1000];
int main(){
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
int n;
int maxn = 0;
cin >> n;
for(int i=1;i<=n;i++){
cin >> a[i];
maxn += a[i];
}
for(int i=1;i<=n;i++) cin >> b[i];
for(int i=1;i<=n;i++){
for(int j=0;j<=maxn;j++){
if(j < a[i]){
dp[i][j] = dp[i - 1][j] + b[i];
}else{
dp[i][j] = min(dp[i - 1][j - a[i]], dp[i - 1][j] + b[i]);
}
}
}
int ans = INF;
for(int i=0;i<=maxn;i++){
if(i < dp[n][i]){
ans = min(ans, dp[n][i]);
}else{
ans = min(ans, i);
}
}
cout << ans;
return 0;
}
▲验证
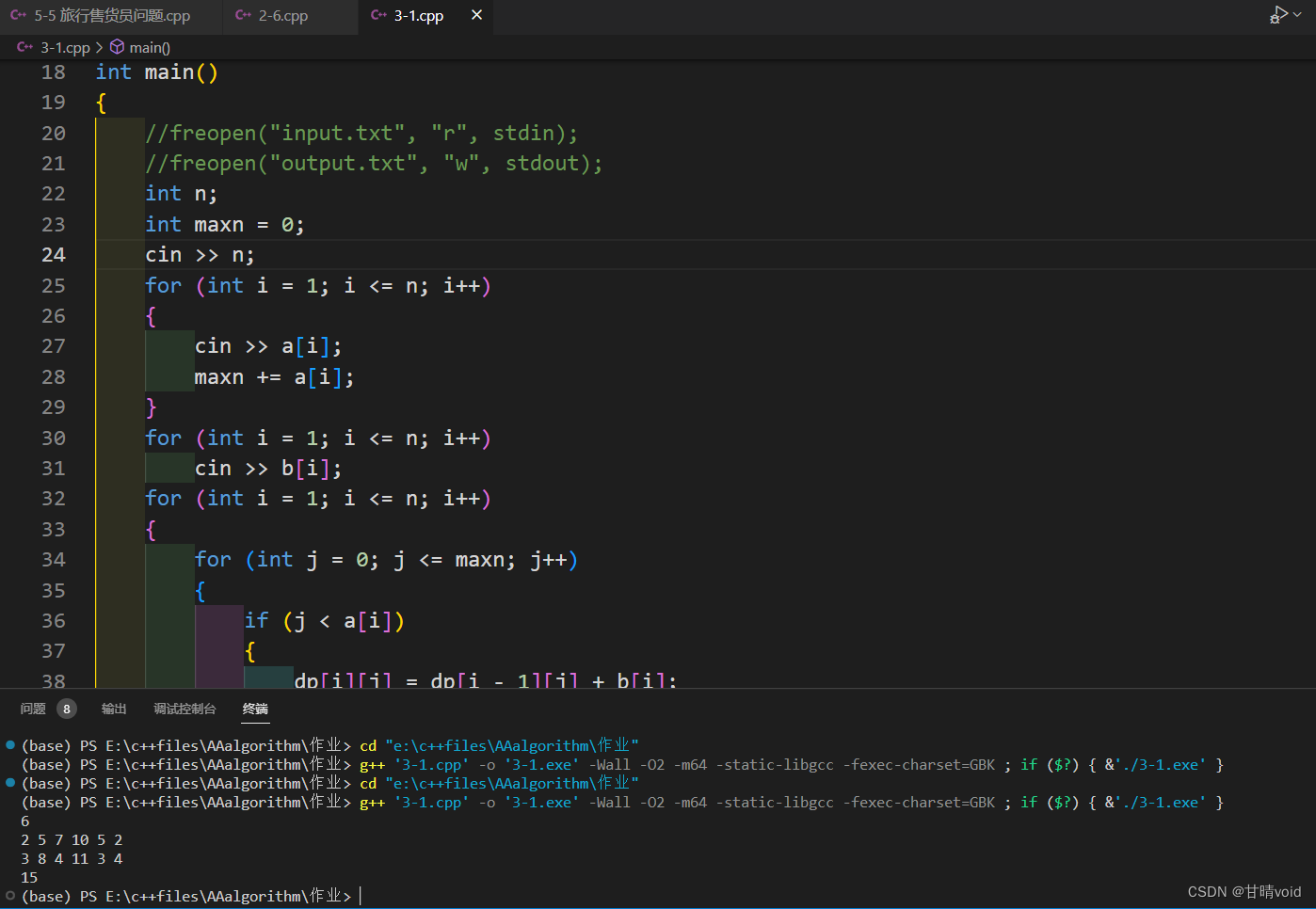
<2>算法实现题 3-4 数字三角形问题
▲问题重述
定一个由n行数字组成的数字三角形,试设计一个算法,计算出从三角形的顶至底的一条路径,使该路径经过的数字总和最大。数据输入: 由文件input.txt提供输入数据。文件的第1行是数字三角形的行数n,(1≤n≤100)。接下来n行是数字三角形各行中的数字。所有数字在0~99之间。结果输出:将计算结果输出到文件output.txt。文件第1行中的数是计算出的最大值。示例:如右图所示,从 7→3→8→7→5的路径产生了最大权值30。
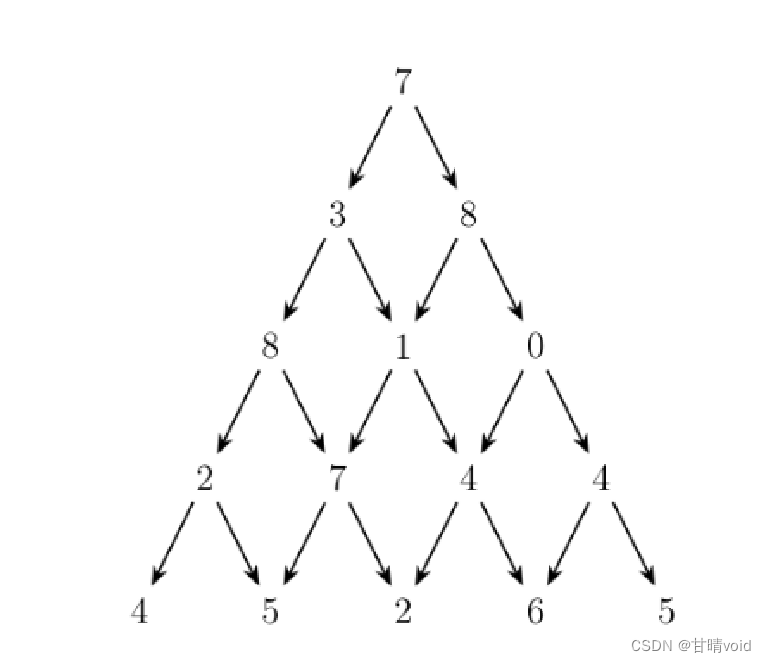
▲解题思路
这道题可以用动态规划来做,重点是表示状态和写状态转移方程设 v[i,j] 为点 (i,j) 上的值,f[i,j] 表示由 (1,1) 到 (i,j) 的路径最大总和,则 f[i,j]=Max{f[i-1,j-1],f[i-1,j]}+v[i,j]。
此处注意“左上角点”对应的是点 (i-1,j-1),右上角对应的是点 (i-1,j)。边界条件更加容易想到,是 f[i][0]=f[0][j]=0 (0<=i,j<=n)。最后还需注意一点。如果浅学过DP可能下意识输出 f[n][n],但根据题目中“到底部任意处结束”可以看出,总和最大的路径可能终结于 (n,1) 到 (n,n) 的任意一点,最后还需要再从中寻找最大的 f[n,j]。
整理思路,首先二重循环输入三角形存储于 a[][] 中,再设一 f[][] 用二重循环求解后,从 f[n][1] 至 f[n][n] 中找到最大值输出。
▲代码
#include<bits/stdc++.h>
using namespace std;
int a[1010][1010],f[1010][1010];
int main(){
int n,s=0;
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
for(int j=1;j<=n;j++) s=max(s,f[n][j]);
cout<<s;
return 0;
}
▲验证:
洛谷P1216 [USACO1.5] [IOI1994]数字三角形 Number Triangles(https://www.luogu.com.cn/problem/P1216)
<3>算法实现题 3-8 最小m段和问题
▲问题重述
给定n个整数组成的序列,现在要求将序列分割成m段,每段子序列中的数在原数列中连续排列。如何分割才能使m段子序列的和的最大值达到最小?
数据读入/读出:
第一行中有2个正整数n和m。正整数n是序列的长度,正整数m是分割的段数。接下来的一行中有n个整数。
▲解题思路
使用dp[i][j]放置将前i个数分成j段的最大最小值。
所以dp[i][1]就是前i个数的和,dp[i][1] = dp[i-1][1] + a[i];
当j>1的时候,假设前k个数为j-1段,从k~i为第j段,所以前j-1段的最大最小值为:dp[k][j-1] (前k个数分为j-1段).
最后一段为:dp[i][1]-dp[k][1] (前i个数的和减去前k个数的和)
这两个值中选取一个最大值,当所有情况讨论结束后,选出结果中最小的作为dp[i][j]的值。
因此,状态转移方程为
dp[i][j] = min{ max{ dp[k][j-1], dp[i][1]-dp[k][1] } } (0<k<i)
▲代码
#include <iostream>
using namespace std;
int dp[500][500];
int t[500];
void solve(int n, int m)
{
int i, j, k, temp, maxt;
for (i = 1; i <= n; i++)
dp[i][1] = dp[i - 1][1] + t[i];
for (j = 2; j <= m; j++)
{
for (i = j; i <= n; i++)
{
for (k = 1, temp = INT_MAX; k < i; k++)
{
maxt = max(dp[i][1] - dp[k][1], dp[k][j - 1]);
if (temp > maxt)
temp = maxt;
}
dp[i][j] = temp;
}
}
}
int main()
{
int n, m;
cin >> n >> m;
if ((n < m) || (n == 0))
{
cout << 0 << endl;
return 0;
}
for (int i = 1; i <= n; i++)
cin >> t[i];
solve(n, m);
cout << dp[n][m] << endl;
}
▲验证
<4>算法实现题 3-25 m处理器问题
▲问题重述

▲解题思路

▲代码
#include <cmath>
#include <iostream>
using namespace std;
double g[500][500];
double t[500];
int n, m;
double f(int a, int b)
{
double ret = 0;
for (int i = a; i <= b; i++)
{
ret += (t[i] * t[i]);
}
return sqrt(ret);
}
double solve()
{
int i, j, k;
double tmp, maxt;
tmp = f(n - 1, n - 1);
for (i = n - 1; i >= 0; i--)
{
if (f(i, i) > tmp)
tmp = f(i, i);
g[i][1] = f(i, n - 1);
if (n - i <= m)
g[i][n - i] = tmp;
}
for (i = n - 1; i >= 0; i--)
{
for (k = 2; k <= m; k++)
{
for (j = i, tmp = INT_MAX; j <= n - k; j++)
{
maxt = max(f(i, j), g[j + 1][k - 1]);
if (tmp > maxt)
tmp = maxt;
}
g[i][k] = tmp;
}
for (k = n - i + 1; k <= m; k++)
g[i][k] = g[i][n - i];
}
return g[0][m];
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> t[i];
}
cout << solve() << endl;
}
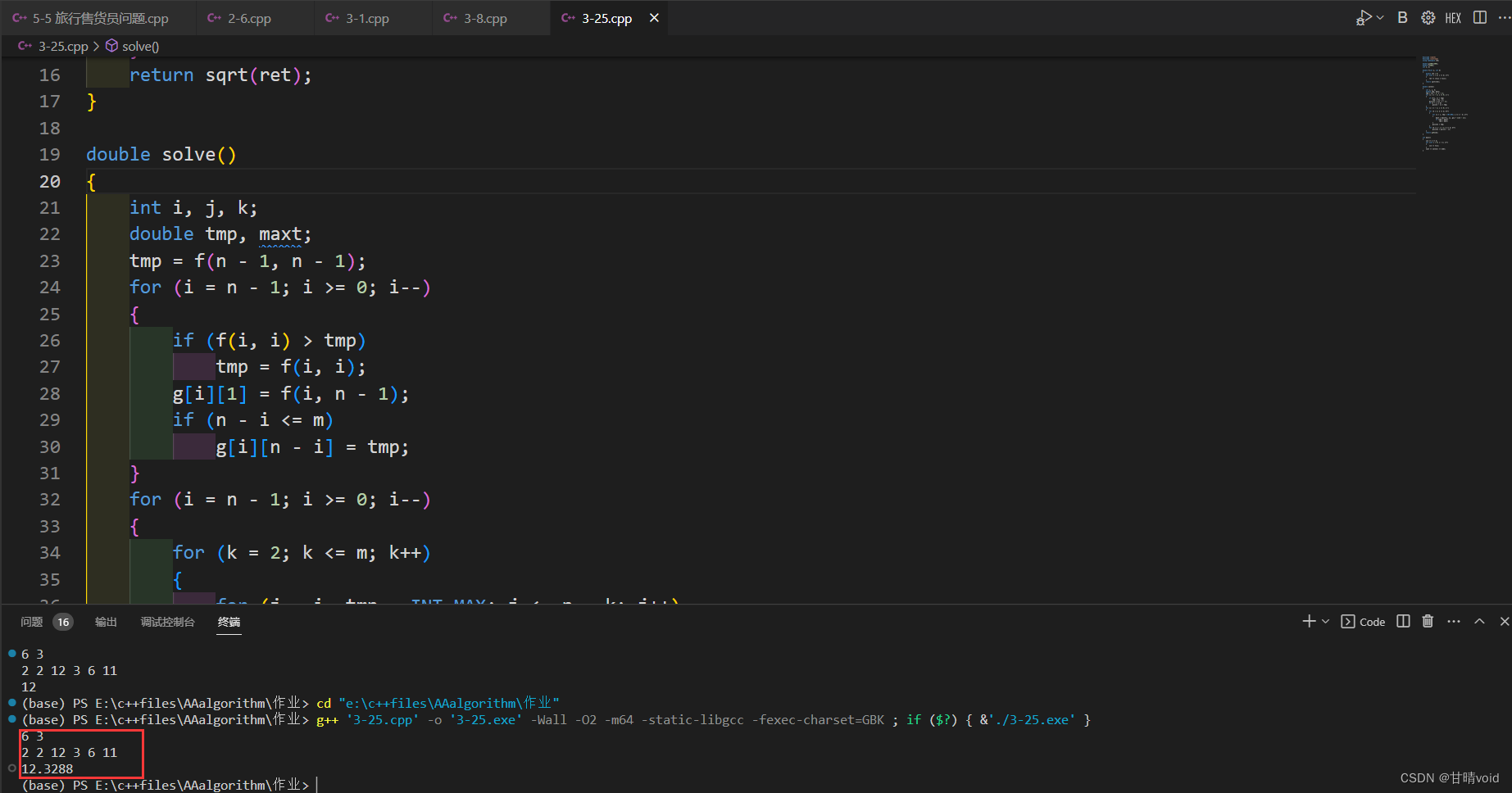
▲验证