目录
1.添加字符
2.数组变换
3.装箱问题
常规一维优化:
1.添加字符
链接
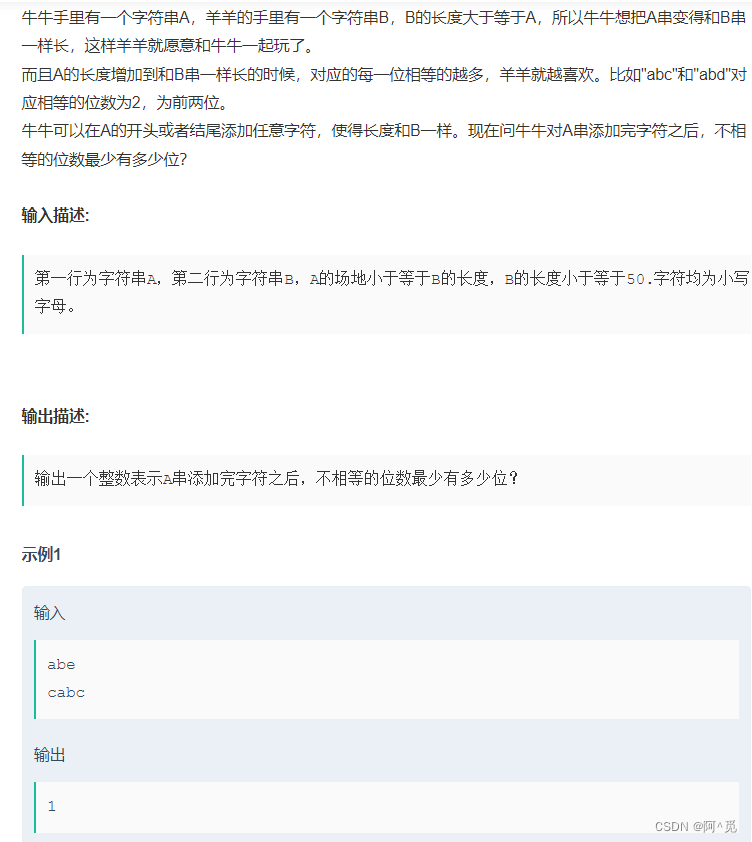
因为lenA <= lenB <= 50,因此可以无脑暴力解题:
遍历所有符合条件的匹配方法,找出最小的不同的数量,即最大的相同的数量
#include <iostream>
using namespace std;
int main() {
string A;
string B;
cin >> A >> B;
int c1 = A.size();
int c2 = B.size();
int cnt = 0;
if (c1 == c2)
{
for (int i = 0; i < c1; i++)
{
if (A[i] != B[i])
cnt++;
}
cout << cnt << endl;
}
else
{
int dif = c2 - c1;
int max_n = 0;
for (int i = 0; i <= dif; ++i)
{
cnt = 0;
int j = 0;
int k = i;
while (j < c1)
{
if (A[j] == B[k])
cnt++;
j++;
k++;
}
max_n = max(max_n, cnt);
}
cout << c1 - max_n << endl;
}
return 0;
}2.数组变换
链接
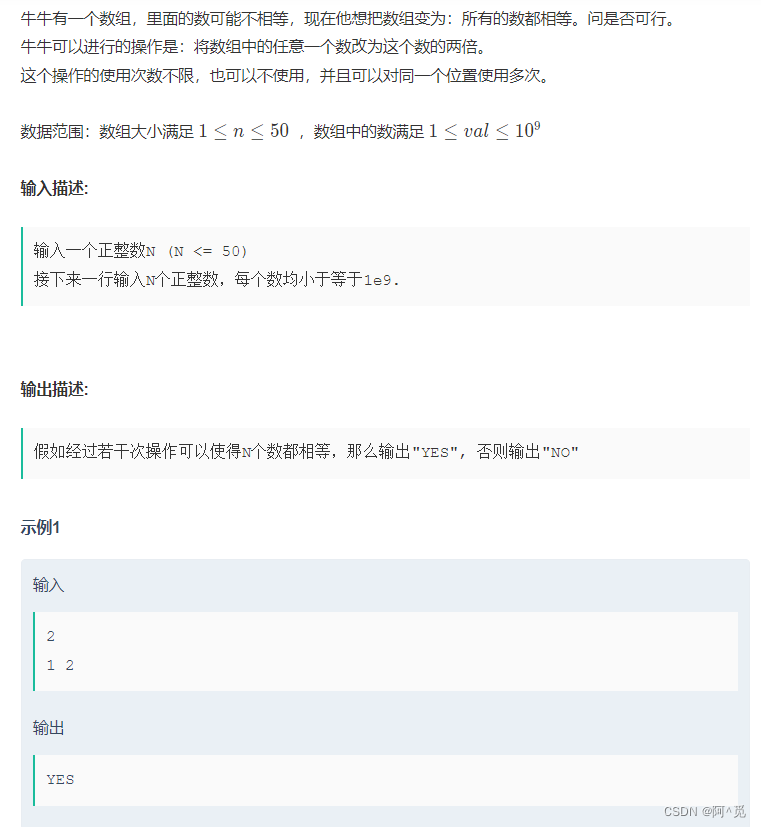
判断是否为2的n次方就好了。
#include <iostream>
using namespace std;
int arr[60];
int main() {
int n;
cin >> n;
int maxn = 0;
int x;
for (int i = 1; i <= n; ++i)
{
cin >> x;
arr[i] = x;
maxn = max(maxn, x);
}
for (int i = 1; i <= n; ++i)
{
if (!((maxn / arr[i]) % 2 == 0 || arr[i] == maxn))
{
cout << "NO" << endl;
return 0;
}
}
cout << "YES" << endl;
return 0;
}3.装箱问题
链接
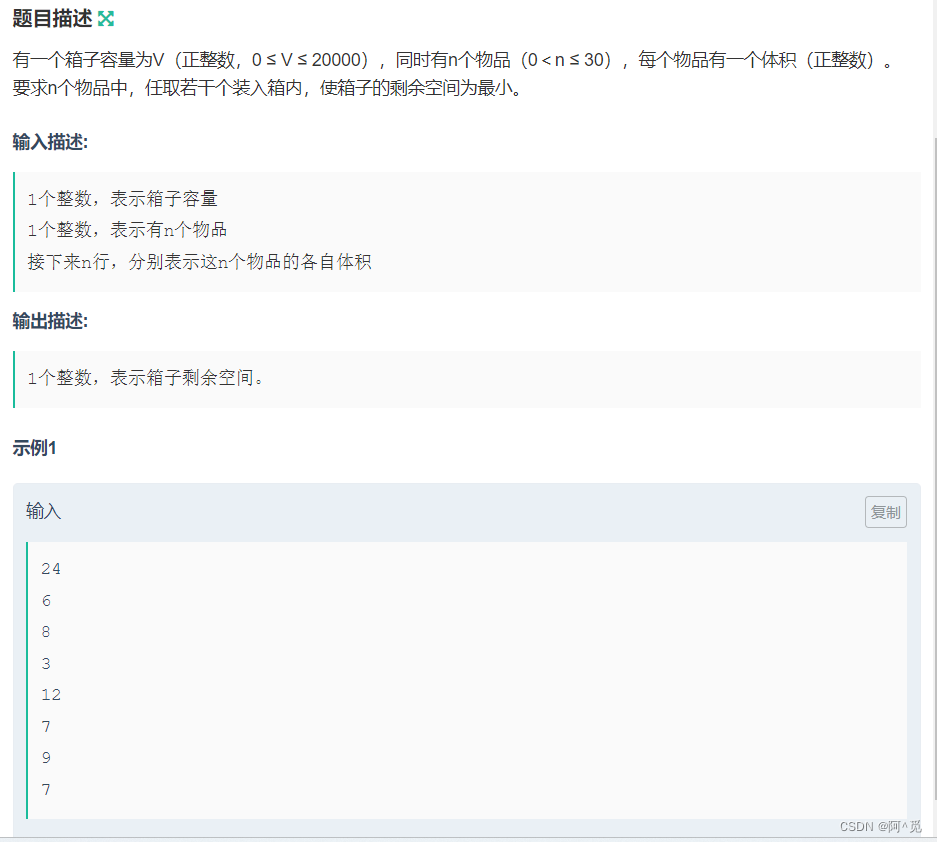
01背包dp问题:
讲题意逆向转化为使装入的体积最大更好求解,最后返回时返回V - dp[n][V]即可。
#include <iostream>
using namespace std;
int V, n;
int v[20010];
int dp[40][20010];
int main()
{
cin >> V >> n;
for (int i = 1; i <= n; ++i)
cin >> v[i];
// 填表
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i - 1][j];
if (j >= v[i])
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + v[i]);
}
}
cout << V - dp[n][V] << endl;
return 0;
}常规一维优化:
#include <iostream>
using namespace std;
int V, n;
int v[20010];
int dp[20010];
int main()
{
cin >> V >> n;
for (int i = 1; i <= n; ++i)
cin >> v[i];
// 填表
for (int i = 1; i <= n; ++i)
for (int j = V; j >= v[i]; --j)
dp[j] = max(dp[j], dp[j - v[i]] + v[i]);
cout << V - dp[V] << endl;
return 0;
}