本篇为本科课程《电力系统稳态分析》的笔记。
本篇为这一章的第一篇笔记。下一篇传送门。
实际中的大规模电力系统包含成百上千个节点、发电机组和负荷,网络是复杂的,需要建立复杂电力系统的同一潮流数学模型,借助计算机进行求解。
简介
计算机算法发展历程
- 1956,高斯法,对初值不敏感,收敛慢。
- 1967,阻抗法,收敛性好,主要基于公式 U ˙ = Z I ˙ \dot{U}=Z\dot{I} U˙=ZI˙计算。
- 1967,牛顿法,使用雅可比矩阵,该矩阵在迭代中会变化。
- 1973,PQ分解法,可以快速解耦,所用雅可比矩阵是一个常数矩阵,P代表的是相角,Q代表的是幅值。
所用软件
- PSASP:电力系统分析综合程序,为国产软件。
- BPA
- PTI
- PSSIE
- Digsilent
- PSCAD/EMTDC
电力网络方程
节点电压方程
可以用于计算的网络方程有两种,一种是回路电流方程,另一种是节点电压方程,实际中使用的是节点电压方程,因为:
- 电力系统接地支路多,回路电流所列方程比节点电压所列方程要多。
- 电力系统的网络较为难找。
- 电力系统希望求出的是电压,而节点电压方程直接就可求出。
如下图所示为一个简单的电网。
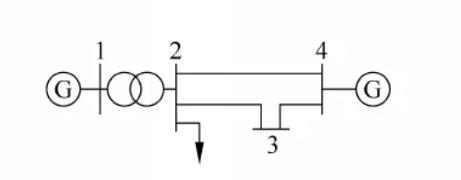
略去变压器的励磁功率和线路电容,复合用阻抗表示,就可以得到一个5节点(包括接地节点)和7条支路的等值电路,如下图所示:
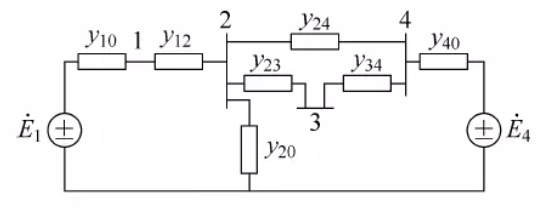
将节点1和节点4的电压源变换成电流源,可以得到下面的等值电路:
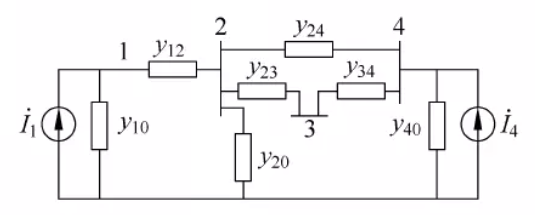
其中 I ˙ 1 = y 10 E ˙ 1 \dot{I}_1=y_{10}\dot{E}_1 I˙1=y10E˙1, I ˙ 4 = y 40 E ˙ 4 \dot{I}_4=y_{40}\dot{E}_4 I˙4=y40E˙4。
可以根据等值电路列出节点电压方程:
{
y
10
V
˙
1
+
y
12
(
V
˙
1
−
V
˙
2
)
=
I
˙
1
y
12
(
V
˙
2
−
V
˙
1
)
+
y
20
V
˙
2
+
y
23
(
V
˙
2
−
V
˙
3
)
+
y
24
(
V
˙
2
−
V
˙
4
)
=
0
y
23
(
V
˙
3
−
V
˙
2
)
+
y
34
(
V
˙
3
−
V
˙
4
)
=
0
y
24
(
V
˙
4
−
V
˙
2
)
+
y
34
(
V
˙
4
−
V
˙
3
)
+
y
40
V
˙
4
=
I
˙
4
\begin{cases}y_{10}\:\dot{V}_1+y_{12}\:(\dot{V}_1-\dot{V}_2\:)=\dot{I}_1\\y_{12}\:(\dot{V}_2-\dot{V}_1\:)+y_{20}\:\dot{V}_2+y_{23}\:(\dot{V}_2-\dot{V}_3\:)+y_{24}\:(\dot{V}_2-\dot{V}_4\:)=0\\y_{23}\:(\dot{V}_3-\dot{V}_2\:)+y_{34}\:(\dot{V}_3-\dot{V}_4\:)=0\\y_{24}\:(\dot{V}_4-\dot{V}_2\:)+y_{34}\:(\dot{V}_4-\dot{V}_3\:)+y_{40}\:\dot{V}_4\:=\:\dot{I}_4\end{cases}
⎩
⎨
⎧y10V˙1+y12(V˙1−V˙2)=I˙1y12(V˙2−V˙1)+y20V˙2+y23(V˙2−V˙3)+y24(V˙2−V˙4)=0y23(V˙3−V˙2)+y34(V˙3−V˙4)=0y24(V˙4−V˙2)+y34(V˙4−V˙3)+y40V˙4=I˙4
对方程做出变换,得到:
{
Y
11
V
˙
1
+
Y
12
V
˙
2
=
I
˙
1
Y
21
V
˙
1
+
Y
22
V
˙
2
+
Y
23
V
˙
3
+
Y
24
V
˙
4
=
0
Y
32
V
˙
2
+
Y
33
V
˙
3
+
Y
34
V
˙
4
=
0
Y
42
V
˙
2
+
Y
43
V
˙
3
+
Y
44
V
˙
4
=
I
˙
4
\begin{cases}Y_{11}\:\dot{V}_1+Y_{12}\:\dot{V}_2=\dot{I}_1\\Y_{21}\:\dot{V}_1+Y_{22}\:\dot{V}_2+Y_{23}\:\dot{V}_3+Y_{24}\:\dot{V}_4=0\\Y_{32}\:\dot{V}_2+Y_{33}\:\dot{V}_3+Y_{34}\:\dot{V}_4=0\\Y_{42}\:\dot{V}_2+Y_{43}\:\dot{V}_3+Y_{44}\:\dot{V}_4=\:\dot{I}_4\end{cases}
⎩
⎨
⎧Y11V˙1+Y12V˙2=I˙1Y21V˙1+Y22V˙2+Y23V˙3+Y24V˙4=0Y32V˙2+Y33V˙3+Y34V˙4=0Y42V˙2+Y43V˙3+Y44V˙4=I˙4
其中, Y 11 = y 10 + y 12 ; Y 22 = y 20 + y 12 + y 23 + y 24 ; Y 33 = y 23 + y 34 ; Y 44 = y 40 + y 24 + y 34 ; Y 12 = Y 21 = − y 12 ; Y 23 = Y 32 = − y 23 ; Y 24 = Y 42 = − y 24 ; Y 34 = Y 43 = − y 34 Y_{11}=y_{10}+y_{12}\:;\:Y_{22}=y_{20}+y_{12}+y_{23}+y_{24}\:;\:Y_{33}=y_{23}+y_{34}\:;\:Y_{44}=y_{40}+y_{24}+y_{34}\:;\:Y_{12}=Y_{21}=-\:y_{12}\:;\:Y_{23}=Y_{32}=-\:y_{23}\:;\:Y_{24}=Y_{42}=-\:y_{24}\:;\:Y_{34}=Y_{43}=-\:y_{34}\: Y11=y10+y12;Y22=y20+y12+y23+y24;Y33=y23+y34;Y44=y40+y24+y34;Y12=Y21=−y12;Y23=Y32=−y23;Y24=Y42=−y24;Y34=Y43=−y34。
一般的,对于n个节点(不包含大地节点)的电网而言,当以大地节点(n+1节点)为参考的时候,可以列出n阶的节点电压方程:
{
Y
11
V
˙
1
+
Y
12
V
˙
2
+
⋯
+
Y
1
n
V
˙
n
=
I
˙
1
Y
21
V
˙
1
+
Y
22
V
˙
2
+
⋯
+
Y
2
n
V
˙
n
=
I
˙
2
⋮
⋮
⋮
Y
n
1
V
˙
1
+
Y
n
2
V
˙
2
+
⋯
+
Y
n
n
V
˙
n
=
I
˙
n
\begin{cases} Y_{11}\:\dot{V}_1+Y_{12}\:\dot{V}_2+\cdots+Y_{1n}\:\dot{V}_n=\:\dot{I}_1\\ Y_{21}\:\dot{V}_1+Y_{22}\:\dot{V}_2+\cdots+Y_{2n}\:\dot{V}_n=\:\dot{I}_2\\ \vdots \hspace{2cm} \vdots \hspace{2cm} \vdots\\ Y_{n1}\:\dot{V}_1+Y_{n2}\:\dot{V}_2+\cdots+Y_{nn}\:\dot{V}_n=\dot{I}_n \end{cases}
⎩
⎨
⎧Y11V˙1+Y12V˙2+⋯+Y1nV˙n=I˙1Y21V˙1+Y22V˙2+⋯+Y2nV˙n=I˙2⋮⋮⋮Yn1V˙1+Yn2V˙2+⋯+YnnV˙n=I˙n
将上面的方程组写成矩阵形式:
[
Y
11
Y
12
⋯
Y
1
n
Y
21
Y
22
⋯
Y
2
n
⋮
⋮
⋮
⋮
Y
n
1
Y
n
2
⋯
Y
n
n
]
[
V
˙
1
V
˙
2
⋮
V
˙
n
]
=
[
I
˙
1
I
˙
2
⋮
I
˙
n
]
\begin{bmatrix}Y_{11}&Y_{12}&\cdots&Y_{1n}\\Y_{21}&Y_{22}&\cdots&Y_{2n}\\\vdots&\vdots&\vdots&\vdots\\Y_{n1}&Y_{n2}&\cdots&Y_{nn}\end{bmatrix}\begin{bmatrix}\dot{V}_1\\\dot{V}_2\\\vdots\\\dot{V}_n\end{bmatrix}=\begin{bmatrix}\dot{I}_1\\\dot{I}_2\\\vdots\\\dot{I}_n\end{bmatrix}
Y11Y21⋮Yn1Y12Y22⋮Yn2⋯⋯⋮⋯Y1nY2n⋮Ynn
V˙1V˙2⋮V˙n
=
I˙1I˙2⋮I˙n
简写作:
Y
V
˙
=
I
˙
\boldsymbol{Y}\boldsymbol{\dot{V}}=\boldsymbol{\dot{I}}
YV˙=I˙
写成求和形式即为:
I
˙
i
=
∑
j
∈
i
Y
i
j
V
˙
j
(
i
=
1
,
…
,
n
)
\dot{I}_i=\sum_{j\in i}Y_{ij}\dot{V}_j\quad(i=1,\dots,n)
I˙i=j∈i∑YijV˙j(i=1,…,n)
其中, I ˙ \dot{I} I˙是各个节点注入电流所组成的向量, I ˙ = [ I ˙ 1 … I ˙ i … I ˙ n ] T \boldsymbol{\dot{I}}=[\boldsymbol{\dot{I}}_1\quad\dots\quad\boldsymbol{\dot{I}}_i\quad\dots\quad\boldsymbol{\dot{I}}_n]^T I˙=[I˙1…I˙i…I˙n]T; V ˙ \boldsymbol{\dot{V}} V˙是各个节点电压所组成的向量, V ˙ = [ V ˙ 1 … V ˙ i … V ˙ n ] T \boldsymbol{\dot{V}}=[\dot{V}_1\quad\dots\quad\boldsymbol{\dot{V}}_i\quad\dots\quad\boldsymbol{\dot{V}}_n]^T V˙=[V˙1…V˙i…V˙n]T。 Y \boldsymbol{Y} Y是网络的节点导纳矩阵。
节点导纳矩阵的对角线元素 Y i i Y_{ii} Yii是节点i的自导纳,其值等于该节点所连支路的导纳之和;非对角元素 Y i j Y_{ij} Yij是节点i和节点j之间的互导纳,其值等于所连支路导纳的负值。
节点导纳矩阵元素的物理意义
对于节点电压方程,令
V
˙
k
≠
0
,
V
˙
j
=
0
(
j
=
1
,
2
,
⋯
n
,
j
≠
k
)
\dot{V}_{k}\neq0,\dot{V}_{j}=0(j=1,2,\cdots n,j\neq k)
V˙k=0,V˙j=0(j=1,2,⋯n,j=k),那么就有:
Y
i
k
V
˙
k
=
I
˙
i
(
i
=
1
,
2
,
⋯
,
n
)
Y_{ik}\:\dot{V}_k\:=\:\dot{I}_i\quad(i\:=\:1,2,\cdots,n)
YikV˙k=I˙i(i=1,2,⋯,n)
即:
Y
i
k
=
I
˙
i
V
˙
k
∣
V
˙
j
=
0
,
j
≠
k
Y_{ik}=\frac{\dot{I}_i}{\dot{V}_k}\Bigg|_{\dot{V}_j=0,j\neq k}
Yik=V˙kI˙i
V˙j=0,j=k
- 当 k = i k=i k=i时,网络中除了节点i之外的所有节点都接地的时候,从节点i注入网络的电流和节点i的电压之比,就是节点i的自导纳 Y i i Y_{ii} Yii,
- 当 k ≠ i k\neq i k=i时,网络中除了节点k之外的所有节点都接地的时候,从节点i注入网络的电流和节点k的电压之比,就是节点i,k之间的互导纳 Y i k Y_{ik} Yik。互导纳有关系 Y i k = Y k i Y_{ik}=Y_{ki} Yik=Yki。如果节点i和k之间没有直接连接,那么有 Y i k = 0 Y_{ik}=0 Yik=0。
从上面的分析可见,节点导纳矩阵的特点是:
- 节点导纳矩阵为 n × n n\times n n×n阶的复数矩阵,当电网至少有一条接地支路的时候就是非奇异矩阵。
- 节点导纳矩阵式对称矩阵,即 Y i k = Y k i Y_{ik}=Y_{ki} Yik=Yki,计算机存储的时候只需要存一半。
- 如果节点之间没有直接连接的支路,那么有 Y i k = 0 Y_{ik}=0 Yik=0。所以矩阵中存在着很多的0元素,这类矩阵叫做稀疏矩阵。
节点导纳矩阵的形成和修正
实际的电力系统所包含节点成千上万,通常采用追加支路法来形成导纳矩阵。做法是:
- 先给节点进行编号,程序形成了一个空的导纳矩阵,所有都是零。
- 然后针对第一条支路,修正其自导纳的值,然后再修正其互导纳的值。
- 对于第二条及以后得支路,采用相同的方法进行修正,直到所有支路都处理完为止。
当电力系统中网络接线改变的时候,需要修改节点导纳矩阵。不需要重新建立矩阵,只需要做个别元素的修正就可以。
- 从网络的节点i引出了一条导纳为
y
i
k
y_{ik}
yik的新支路,同时新增一个节点k,如下图所示:
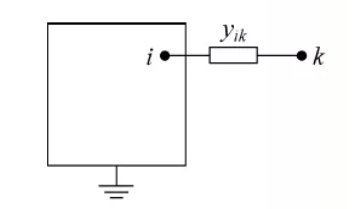
因为节点数增加了一个,所以矩阵要增加一行一列,新增的对角元素就是节点k的自导纳 Y k k = y i k Y_{kk}=y_{ik} Ykk=yik。新增的非对角元素中,只有 Y i k = Y k i = − y i k Y_{ik}=Y_{ki}=-y_{ik} Yik=Yki=−yik,其余的非对角元素都是零。在矩阵的原有部分,只有节点i的自导纳有变化量为 Δ Y i i = y i k \Delta Y_{ii}=y_{ik} ΔYii=yik。 - 在原有的节点i,j之间增加一条支路,其导纳为
y
i
j
y_{ij}
yij,如下图所示:
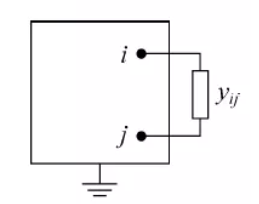
矩阵阶数不变,节点i和j的自导纳有变化量 Δ Y i i = Δ Y j j = y i j \Delta Y_{ii}=\Delta Y_{jj}=y_{ij} ΔYii=ΔYjj=yij。他们的互导纳有变化量 Δ Y i j = Δ Y j i = − y i j \Delta Y_{ij}=\Delta Y_{ji}=-y_{ij} ΔYij=ΔYji=−yij。其余元素不发生变化。 - 在原有的节点i,j之间切除一条已有支路,其导纳为 y i j y_{ij} yij。这相当于节点i,j之间增加一条导纳为 − y i j -y_{ij} −yij支路,所以节点i和j的自导纳有变化量 Δ Y i i = Δ Y j j = − y i j \Delta Y_{ii}=\Delta Y_{jj}=-y_{ij} ΔYii=ΔYjj=−yij。他们的互导纳有变化量 Δ Y i j = Δ Y j i = y i j \Delta Y_{ij}=\Delta Y_{ji}=y_{ij} ΔYij=ΔYji=yij。其余元素不发生变化。
变压器的导纳阵
变压器节点如下所示:

变压器 Π \Pi Π型等值电路如下图所示:

则是一个
2
×
2
2\times2
2×2的导纳阵,自导纳为:
Y
i
i
=
1
k
Y
T
+
k
−
1
k
Y
T
=
Y
T
(与
k
无关)
Y
j
j
=
1
k
Y
T
+
1
−
k
k
2
Y
T
=
1
k
2
Y
T
(与
k
有关)
Y_{ii}=\frac{1}{k}Y_T+\frac{k-1}{k}Y_T=Y_T\quad(与k无关)\\\\ Y_{jj}=\frac{1}{k}Y_T+\frac{1-k}{k^2}Y_T=\frac{1}{k^2}Y_T\quad(与k有关)
Yii=k1YT+kk−1YT=YT(与k无关)Yjj=k1YT+k21−kYT=k21YT(与k有关)
互导纳为:
Y
i
j
=
Y
j
i
=
−
1
k
Y
T
Y_{ij}=Y_{ji}=-\frac{1}{k}Y_T
Yij=Yji=−k1YT
当变压器的变比发生变化的时候,
k
→
k
′
k\rightarrow k'
k→k′,那么导纳阵发生的变化为:
Δ
Y
i
i
=
0
Δ
Y
j
j
=
−
1
k
2
Y
T
+
1
k
′
2
Y
T
Δ
Y
i
j
=
1
k
Y
T
−
f
r
a
c
1
k
′
Y
T
\Delta Y_{ii}=0\\\\ \Delta Y_{jj}=-\frac{1}{k^2}Y_T+\frac{1}{k'^2}Y_T\\\\ \Delta Y_{ij}=\frac{1}{k}Y_T-frac{1}{k'}Y_T
ΔYii=0ΔYjj=−k21YT+k′21YTΔYij=k1YT−frac1k′YT
节点阻抗矩阵表示的网络方程
阻抗矩阵形式的网络方程
若节点导纳矩阵
Y
\boldsymbol{Y}
Y的逆矩阵存在
Y
−
1
\boldsymbol{Y}^{-1}
Y−1,那么可以得到用节点阻抗矩阵形式表示的网络方程:
V
˙
=
Z
I
˙
\boldsymbol{\dot{V}}=\boldsymbol{Z}\boldsymbol{\dot{I}}
V˙=ZI˙
其中, Z = Y − 1 \boldsymbol{Z}=\boldsymbol{Y}^{-1} Z=Y−1就是节点的阻抗矩阵,阻抗矩阵的对角元素 Z i i Z_{ii} Zii就是节点i的自阻抗,非对角元素 Z i j Z_{ij} Zij就是节点i,j的互阻抗。
节点阻抗矩阵的物理意义和特点
当对节点i注入电位电流
I
˙
i
=
1
\dot{I}_i=1
I˙i=1,其余节点不注入电流
I
˙
j
=
0
(
j
≠
i
;
j
=
1
,
…
,
n
)
\dot{I}_j=0\quad(j\neq i;j=1,\dots,n)
I˙j=0(j=i;j=1,…,n),就有:
U
˙
i
=
Z
i
i
U
˙
j
=
Z
j
i
(
j
≠
i
;
j
=
1
,
…
,
n
)
\dot{U}_i=Z_{ii}\\\\ \dot{U}_j=Z_{ji}\\\\ (j\neq i;j=1,\dots,n)
U˙i=ZiiU˙j=Zji(j=i;j=1,…,n)
阻抗矩阵有以下的特点:
- 阻抗矩阵是 n × n n\times n n×n阶对称矩阵。
- 是各元素为复数的满阵,没有一个零元素。
- 若电网没有接地支路,那么导纳阵就是奇异阵,不存在阻抗矩阵。
- 阻抗矩阵不宜生成。
- 根据定义,自阻抗 Z i i Z_{ii} Zii是节点i和大地之间一端口的入端阻抗。
潮流计算的节点功率方程和节点分类
节点方程式是潮流计算的基础,已知网络矩阵后,如果能够给出电流源和电压源的值,那么直接求解网络方程就,可以得到网络内电压和电流分布情况。但是在实际的潮流计算中,通常已知的条件是发电机的输出功率或机端电压、负荷的功率等,在网络的运行状态求出之前,无论是电源电压还是节点注入电流,都无法确定。
根据复功率公式
S
~
=
U
˙
I
˙
∗
\widetilde{S}=\dot{U}\dot{I}^*
S
=U˙I˙∗,可得:
I
˙
i
=
(
S
~
i
U
˙
i
)
∗
=
P
i
−
j
Q
i
U
˙
i
∗
\dot{I}_i=\left(\frac{\widetilde{S}_i}{\dot{U}_i}\right)^*=\frac{P_i-jQ_i}{\dot{U}_i^*}
I˙i=(U˙iS
i)∗=U˙i∗Pi−jQi
上面这个公式对于任何一个节点i都是成立的。其中, U ˙ i , I ˙ i \dot{U}_i,\dot{I}_i U˙i,I˙i分别为节点i的电压和注入电流复数, P i , j Q i P_i,jQ_i Pi,jQi分别为节点i的注入有功功率和无功功率。如果这个节点上同时接有发电机 S ~ G i = P G i + j Q G i \widetilde{S}_{Gi}=P_{Gi}+jQ_{Gi} S Gi=PGi+jQGi和负荷 S ~ L i = P L i + j Q L i \widetilde{S}_{Li}=P_{Li}+jQ_{Li} S Li=PLi+jQLi, P i , j Q i P_i,jQ_i Pi,jQi发电机注入功率和负荷流出功率的差值。即 P i + j Q i = ( P G i − P L i ) + j ( Q G i − Q L i ) P_i+jQ_i=(P_{Gi}-P_{Li})+j(Q_{Gi}-Q_{Li}) Pi+jQi=(PGi−PLi)+j(QGi−QLi)
将上式带入节点电压方程,可得:
P
i
−
j
Q
i
U
i
∗
=
∑
j
=
1
n
Y
i
j
U
j
(
i
=
1
,
2
,
⋯
,
n
)
\frac{P_i-\mathrm{j}Q_i}{U_i^*}=\sum_{j=1}^nY_{ij}U_j\quad(i=1,2,\cdots,n)
Ui∗Pi−jQi=j=1∑nYijUj(i=1,2,⋯,n)
将
U
i
∗
U_i^*
Ui∗乘到右边,然后两边同时取共轭,可得:
P
i
+
j
Q
i
=
U
i
∑
j
=
1
n
Y
i
j
∗
U
j
∗
(
i
=
1
,
2
,
⋯
,
n
)
P_i+\mathrm{j}Q_i=U_i\sum_{j=1}^nY_{ij}^*U_j^*\quad(i=1,2,\cdots,n)
Pi+jQi=Uij=1∑nYij∗Uj∗(i=1,2,⋯,n)
上式就是电网的统一潮流方程,是一个复数方程,将实部和虚部分开,每个节点可以得到两个实数方程,但有四个变量,分别为节点注入有功功率P,节点注入无功功率Q,节点电压幅值U,和电压相位 θ \theta θ,必须要给定其中两个,然后使用两个方程求出剩下两个。
电压用极坐标形式表示的节点功率方程
将电压相量用极坐标形式表示为: U ˙ i = U i e j θ i ( i = 1 , ⋯ , n ) \dot{U}_i=U_ie^{j\theta_i}\quad(i=1,\cdots,n) U˙i=Uiejθi(i=1,⋯,n)。其中, U i , θ i U_i,\theta_i Ui,θi分别为节点i电压的有效值和相角。
将导纳矩阵中的元素用直角坐标形式表示为: Y i j = G i j + j B i j ( i , j = 1 , ⋯ , n ) Y_{ij}=G_{ij}+jB_{ij}\quad(i,j=1,\cdots,n) Yij=Gij+jBij(i,j=1,⋯,n)。
则统一潮流方程可以改写为:
P
i
+
j
Q
i
=
U
i
e
j
θ
i
∑
j
=
1
n
(
G
i
j
−
j
B
i
j
)
U
j
e
j
θ
j
(
i
=
1
,
⋯
,
n
)
P_i+jQ_i=U_ie^{j\theta_i}\sum_{j=1}^n(G_{ij}-jB_{ij})U_je^{j\theta_j}\quad(i=1,\cdots,n)
Pi+jQi=Uiejθij=1∑n(Gij−jBij)Ujejθj(i=1,⋯,n)
将上式中的指数用欧拉公式展开:
e
j
θ
=
cos
θ
+
j
sin
θ
e^{j\theta}=\cos\theta+j\sin\theta
ejθ=cosθ+jsinθ,这样就得到了:
P
i
+
j
Q
i
=
U
i
∑
j
=
1
n
U
j
(
G
i
j
−
j
B
i
j
)
(
cos
θ
i
j
+
sin
θ
i
j
)
(
i
=
1
,
⋯
,
n
)
P_i+jQ_i=U_i\sum_{j=1}^nU_j(G_{ij}-jB_{ij})(\cos\theta_{ij}+\sin\theta_{ij})\quad(i=1,\cdots,n)
Pi+jQi=Uij=1∑nUj(Gij−jBij)(cosθij+sinθij)(i=1,⋯,n)
其中, θ i j \theta_{ij} θij是节点i和j相角之差, θ i j = θ i − θ j \theta_{ij}=\theta_{i}-\theta_{j} θij=θi−θj
分开实部和虚部,得到两个方程:
P
i
=
U
i
∑
j
=
1
n
U
j
(
G
i
j
cos
θ
i
j
+
B
i
j
sin
θ
i
j
)
Q
i
=
U
i
∑
j
=
1
n
U
j
(
G
i
j
sin
θ
i
j
−
B
i
j
cos
θ
i
j
)
(
i
=
1
,
⋯
,
n
)
P_i=U_i\sum_{j=1}^nU_j(G_{ij}\cos\theta_{ij}+B_{ij}\sin\theta_{ij})\\\\ Q_i=U_i\sum_{j=1}^nU_j(G_{ij}\sin\theta_{ij}-B_{ij}\cos\theta_{ij})\\\\ (i=1,\cdots,n)
Pi=Uij=1∑nUj(Gijcosθij+Bijsinθij)Qi=Uij=1∑nUj(Gijsinθij−Bijcosθij)(i=1,⋯,n)
上面两个方程就是电压用极坐标形式表示时候的节点功率方程,简称为功率方程。有n个节点的网络会有2n的方程。
电压用直角坐标系形式表示的节点功率方程
将电压相量用直角坐标形式表示:
U
˙
i
=
e
i
+
j
f
i
(
i
=
1
,
⋯
,
n
)
\dot{U}_i=e_i+jf_i\quad(i=1,\cdots,n)
U˙i=ei+jfi(i=1,⋯,n),然后带入统一潮流方程,经过整理之和可以得到两个直角坐标形式下的节点功率方程:
P
i
=
e
i
∑
j
=
1
n
(
G
i
j
e
i
−
B
i
j
f
j
)
+
f
i
∑
j
=
1
n
(
G
i
j
f
i
+
B
i
j
e
j
)
Q
i
=
f
i
∑
j
=
1
n
(
G
i
j
e
i
−
B
i
j
f
j
)
−
e
i
∑
j
=
1
n
(
G
i
j
f
i
+
B
i
j
e
j
)
(
i
=
1
,
⋯
,
n
)
P_i=e_i\sum_{j=1}^n(G_{ij}e_i-B_{ij}f_j)+f_i\sum_{j=1}^n(G_{ij}f_i+B_{ij}e_j)\\\\ Q_i=f_i\sum_{j=1}^n(G_{ij}e_i-B_{ij}f_j)-e_i\sum_{j=1}^n(G_{ij}f_i+B_{ij}e_j)\\\\ (i=1,\cdots,n)
Pi=eij=1∑n(Gijei−Bijfj)+fij=1∑n(Gijfi+Bijej)Qi=fij=1∑n(Gijei−Bijfj)−eij=1∑n(Gijfi+Bijej)(i=1,⋯,n)
而且有
U
i
2
=
e
i
2
+
f
i
2
(
i
=
1
,
⋯
,
n
)
U_i^2=e_i^2+f_i^2\quad(i=1,\cdots,n)
Ui2=ei2+fi2(i=1,⋯,n)。
可见功率方程为各节点电压实部和虚部的二次方程组。
节点分类
根据电力系统实际运行条件,按照所给定变量的不同,可以分为以下三种类型:
- PQ节点。给定节点的有功功率P和无功功率Q,节点电压幅值 U U U和相角 θ \theta θ是待求量。对应于实际中的纯负荷节点(变电站母线)、有功功率和无功功率都给定的发电机节点(含节点上带有负荷),和既没有负荷又没有发电机的联络节点(有功功率和无功功率都为零),这种节点数量占绝大多数。
- PV节点。给定节点的有功功率P和节点电压幅值U,节点的无功功率Q和电压相角 θ \theta θ是待求量。这种节点必须拥有足够的可调无功容量,用于维持给定的电压幅值,所以也叫电压控制节点。对应于实际中无功功率富裕的发电厂母线以及装有无功补偿装置的变电站母线。
- 平衡节点。潮流计算中,因为实现不知道各节点电压,所以系统的有功损耗和无功损耗不能提前确定,意味着至少有一个节点的有功功率不能给定,那么这个节点就被称为平衡节点或松弛节点。平衡节点一般只有一个,他的电压幅值和相位已经给定,而有功功率和无功功率是待求量,一般选择容量较大的发电机节点,以便功率损耗估计有出入的时候,对他的注入有功功率产生较少的影响。
经过分析可见,确定了所有节点的类型之后,统一潮流方程组的求解就变成了由2n个方程求解2n个变量的非线性代数组求过零解的数学问题。因为平衡节点的电压幅值和相角已经给定,所以他不参与方程的求解。
潮流计算的约束条件
通过求解可以得到一组结果,但这组结果是否能够在现实工程中使用,还得需要经过检验。常用的约束有:
- 所有节点的电压必须满足:
U i m i n ⩽ U i ⩽ U i m a x U_{i\mathrm{min}}\leqslant U_i \leqslant U_{i\mathrm{max}} Uimin⩽Ui⩽Uimax
为了保证电能质量和供电安全。 - 所有电源节点的有功功率和无功功率必须满足:
{ P G i min ⩽ P G i ⩽ P G i max Q G i min ⩽ Q G i ⩽ Q G i max \begin{cases}P_{Gi\min}\leqslant P_{Gi}\leqslant P_{Gi\max}\\\\Q_{Gi\min}\leqslant Q_{Gi}\leqslant Q_{Gi\max}\end{cases} ⎩ ⎨ ⎧PGimin⩽PGi⩽PGimaxQGimin⩽QGi⩽QGimax
所有PQ节点的有功、无功功率和PV节点的有功功率,给定时候必须满足上面条件。所有PV节点无功功率和平衡节点的有功、无功功率需要按照上面的条件进行校验。 - 节点之间的相角差
θ
i
j
\theta_{ij}
θij必须满足:
θ i j = ∣ θ i − θ j ∣ ⩽ θ i j max \theta_{ij}=|\theta_{i}-\theta_{j}|\leqslant\theta_{ij\max} θij=∣θi−θj∣⩽θijmax
为了保证系统运行的稳定性,所以要求线路两端的电压相角差不能大于一定值。