哈希表
- 哈希表
- 1.有效的字母异位词
- 242.有效的字母异位词
- 383.赎金信
- 49.字母异位词分组
- 438.找到字符串中所有字母异位词
- 2.两个数组的交集
- 349.两个数组的交集
- 350.两个数组的交集||
- 3.快乐数202
- 202.快乐数
- 4.两数之和
- 1.两数之和
- 5.四数相加
- 454.四数相加||
- 6.三数之和
- 15.三数之和
- 7.四数之和
- 18.四数之和
哈希表
1.有效的字母异位词
242.有效的字母异位词
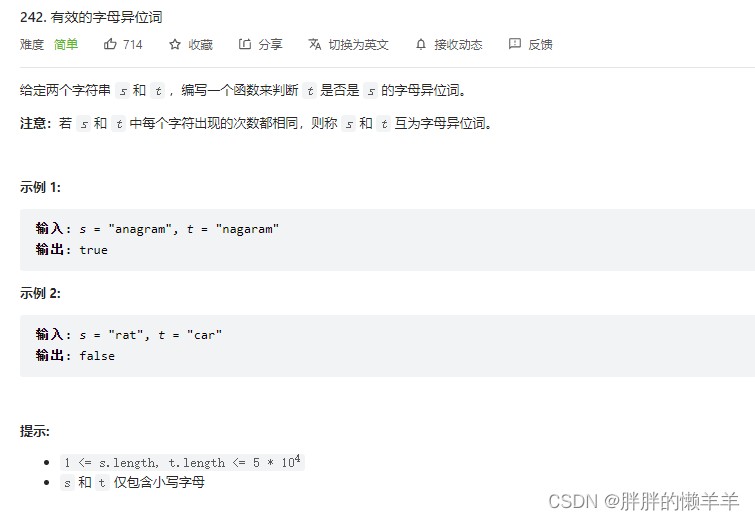
思路: 就是判断两个字符串包含的字母是不是一样的。我们可以用一个数组来存储这些。遍历s的时候把字符出现的个数用数组来存储,遍历t的时候再把相应的个数减去,最后判断数组里边的元素是不是都为0.
public boolean isAnagram(String s, String t) {
int []arr=new int[26];
for(int i=0;i<26;i++) {
arr[i]=0;
}
for(int i=0;i<s.length();i++) {
arr[s.charAt(i)-'a']++;
}
for(int i=0;i<t.length();i++) {
arr[t.charAt(i)-'a']--;
}
for(int i=0;i<26;i++) {
if(arr[i]!=0) {
return false;
}
}
return true;
}
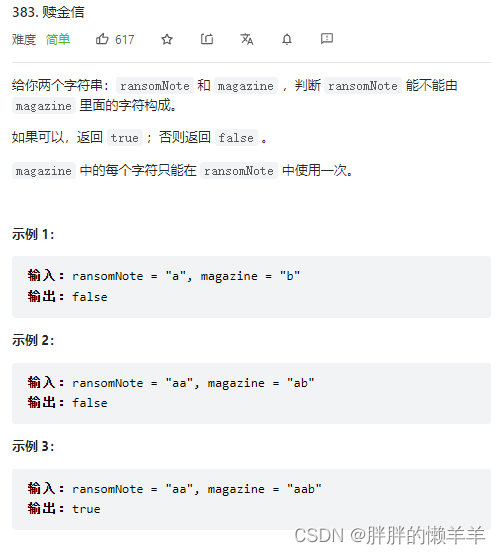
383.赎金信
思路:
和上一题思路一样,这道题只不过是串的范围大小的问题,后边的字符串字母可以多几个。
public boolean canConstruct(String ransomNote, String magazine) {
int []arr=new int[26];
for(int i=0;i<26;i++) {
arr[i]=0;
}
for(int i=0;i<magazine.length();i++) {
arr[magazine.charAt(i)-'a']++;
}
for(int i=0;i<ransomNote.length();i++) {
arr[ransomNote.charAt(i)-'a']--;
}
for(int i=0;i<26;i++) {
if(arr[i]<0) {
return false;
}
}
return true;
}
49.字母异位词分组

思路:
字母异位词就是字母个数相同而排列顺序不同的字符。我们可以把字母排序好的字符串当作键,然后对应的字符串当作值,最后依次输出即可。
public List<List<String>> groupAnagrams(String[] strs) {
Map<String,List<String>> map=new HashMap<String,List<String>>();
for(String str:strs) {
char []array=str.toCharArray();
Arrays.sort(array);
String key=new String(array);
List<String> list=map.getOrDefault(key, new ArrayList<String>());
list.add(str);
map.put(key,list);
}
return new ArrayList<List<String>>(map.values());
}
438.找到字符串中所有字母异位词

思路:
首先将p字符串出现的字符存在字符数组里面,定义distance表示有效字符的个数。
一直在滑动窗口里的字符数组填入right指针指向的数据,当distance满足条件时,此时可以缩小窗口了,即移动左指针,当左右指针的差值恰好等于目标字符的长度时,此时就代表子串找到了。
public static List<Integer> findAnagrams(String s, String p) {
//将原字符串转换成字符数组
char []charArrayS=s.toCharArray();
char []charArrayP=p.toCharArray();
//分别记录窗口里和原字符串字母出现的个数
int []winFreq=new int[26];
int []pFreq=new int[26];
for(char c:charArrayP) {
pFreq[c-'a']++;
}
int distance=0;//窗口里满足条件的字符串的个数
int begin=0;//满足条件的数组的起始位置
int left=0,right=0;//左右指针
List<Integer> result=new ArrayList<>();
while(right<charArrayS.length) {
//当右指针遇见的字符串在tFreq中没有出现,右指针继续往右移动
if(pFreq[charArrayS[right]-'a']==0) {
right++;
continue;
}
//当遇到的这个字符,窗口内的字符个数小于目标字符个数时,distance++
if(winFreq[charArrayS[right]-'a']<pFreq[charArrayS[right]-'a']) {
distance++;
}
winFreq[charArrayS[right]-'a']++;
right++;
while(distance==p.length()) {
if((right-left)==p.length())
{
result.add(left);
}
if(pFreq[charArrayS[left]-'a']==0) {
left++;
continue;
}
if(winFreq[charArrayS[left]-'a']==pFreq[charArrayS[left]-'a']) {
distance--;
}
winFreq[charArrayS[left]-'a']--;
left++;
}
}
return result;
}
2.两个数组的交集
349.两个数组的交集

思路:
用set做:将第一个数组出现的字母存在set里,然后再遍历一次,将第二个数组也在set出现的存在result里即可,result也用set来实现,可以去重。
用数组做:只需要将对应出现的字母标志位置为1即可。
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set1=new HashSet<>();
Set<Integer> result=new HashSet<>();
for(int i:nums1) {
set1.add(i);
}
for(int i:nums2) {
if(set1.contains(i)) {
result.add(i);
}
}
return result.stream().mapToInt(x->x).toArray();
}
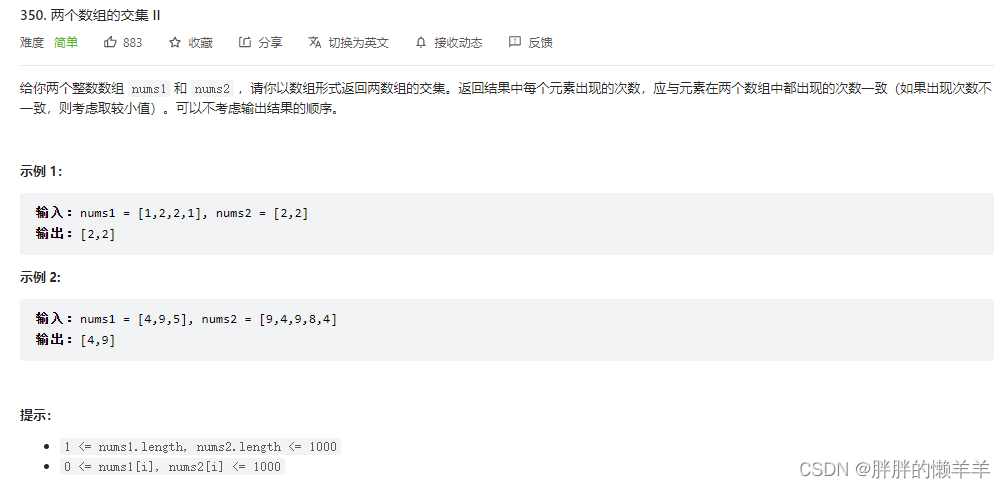
350.两个数组的交集||
思路:
用哈希表分别统计出两个数组每个字母出现的次数,然后用出现次数较小的次数加在结果数组里即可。
public static int[] intersect(int[] nums1, int[] nums2) {
int[] array1=new int[1005];
int[] array2=new int[1005];
List<Integer> result=new ArrayList<>();
for(int i:nums1) {
array1[i]++;
}
for(int i:nums2) {
array2[i]++;
}
for(int i=0;i<array2.length;i++) {
if(array2[i]>0&&array1[i]>0) {
int number=array2[i]<array1[i]?array2[i]:array1[i];
for(int j=0;j<number;j++) {
result.add(i);
}
}
}
return result.stream().mapToInt(x->x).toArray();
}
3.快乐数202
202.快乐数

思路:
这道题的重点就是判断数字是否会出现无限循环的情况,我们可以把每次遍历的数记录起来,然后如果出现同样的数,说明这个数字就不是快乐数。如果没有出现,就让它进入循环即可。
class Solution {
public boolean isHappy(int n) {
Set<Integer>record=new HashSet<Integer>();
while(n!=1&&!record.contains(n)) {
record.add(n);
n=nextNumber(n);
}
return n==1;
}
public int nextNumber(int n) {
int res=0;
while(n>0) {
int index=n%10;
res+=index*index;
n=n/10;
}
return res;
}
}
4.两数之和
1.两数之和

思路:
用哈希表来做,数字作为键,数字下标作为值。这样只需要遍历一遍就可以找到答案。每遍历到一个数,找出target-i是否之前遍历过,如果遍历过就返回两个下标。
至于一个元素出现两次的情况,在hashmap中这种情况,后来出现的会覆盖掉之前出现的数字。题目中要求就是只有一组解,所以这种情况就不用考虑了把。
public int[] twoSum(int[] nums, int target) {
Map<Integer,Integer> maps=new HashMap<>();
for(int i=0;i<nums.length;i++) {
if(maps.containsKey(target-nums[i])) {
return new int[]{maps.get(target-nums[i]),i};
}
maps.put(nums[i], i);
}
return new int[]{0};
}
5.四数相加
454.四数相加||

思路:
将四个数组分成两组,前两个数组a+b的值当成键存在map中,值存这个键出现的次数。然后第二组遍历寻找对应的target值即可。此时的count不应是+1,而是加上map中对应的value值。
public static int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
Map<Integer,Integer> maps=new HashMap<>();
int count=0;
System.out.println(Arrays.toString(nums2));
for(int i=0;i<nums1.length;i++) {
for(int j=0;j<nums2.length;j++) {
maps.put(nums1[i]+nums2[j],maps.getOrDefault(nums1[i]+nums2[j], 0)+1);
}
}
for(int i=0;i<nums3.length;i++) {
for(int j=0;j<nums4.length;j++) {
int target=0-(nums3[i]+nums4[j]);
if(maps.containsKey(target)) {
count+=maps.get(target);
}
}
}
return count;
}
6.三数之和
15.三数之和

思路:
先给原始数组排好序,然后第一次遍历代表a。然后分别用两个指针来找剩下两个数字,当三个数的和大于0时,让右指针往左移,当三个数的和小于0时,让左指针往右移。当满足条件后,将满足条件的数值放进数组里即可。
去重问题:
a去重:用nums[i]和nums[i-1]来比较,因为如果和它后边的数比较会出现正好出现答案而错过去的情况,例如[-1,-1,2].
bc去重:当左指针往右走的时候,遇到和左边数值一样的情况,继续往右走即可。同理,右指针也如此。
public List<List<Integer>> threeSum(int[] nums) {
//保存结果集
List<List<Integer>> result=new ArrayList<List<Integer>>();
//先对数组进行排序
Arrays.sort(nums);
//第一层循环代表数字a
for(int i=0;i<nums.length;i++) {
//第一个数大于0,直接return
if(nums[i]>0) {
return result;
}
//对a进行去重,此时a应该与前一位进行比较,而不是对后一位进行比较
if(i>0&&nums[i]==nums[i-1]) {
continue;
}
int left=i+1;//left指针指向i的右一个
int right=nums.length-1;//right指向末尾
while(left<right) {
if((nums[i]+nums[left]+nums[right])==0) {
result.add(Arrays.asList(nums[i],nums[left],nums[right]));
//对b和c进行去重
while(left<right&&(nums[left]==nums[left+1])) {
left++;
}
while(left<right&&(nums[right]==nums[right-1])) {
right--;
}
left++;
right--;
}else if((nums[i]+nums[left]+nums[right])<0) {
left++;
}else if((nums[i]+nums[left]+nums[right])>0) {
right--;
}
}
}
return result;
}
7.四数之和
18.四数之和

思路
和三数之和思路一样,只不过又多套了一层循环,剪枝操作时要注意负数的情况。
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> result = new ArrayList<List<Integer>>();
Arrays.sort(nums);
for (int k = 0; k < nums.length; k++) {
// 剪枝操作,如果nums[k]大于0,并且nums[k]大于target的话,可以直接return了。为啥要target大于0呢,因为如果是负数的情况,会出现两个数相加越来越小的情况
if (nums[k] > 0 && nums[k]>target) {
return result;
}
// 去重操作,第一层去重k
if (k > 0 && nums[k] == nums[k - 1]) {
continue;
}
for (int i = k + 1; i < nums.length; i++) {
// 第二层剪枝操作 java不用第二层剪枝了
// if ((nums[k] + nums[i]) >=0 &&(nums[k] + nums[i])>target) {
// return result;
// }
// 第二层去重操作
if (i > k + 1 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.length - 1;
while (left < right) {
if ((nums[k] + nums[i] + nums[left] + nums[right]) == target) {
result.add(Arrays.asList(nums[k], nums[i], nums[left], nums[right]));
// 对b和c进行去重
while (left < right && (nums[left] == nums[left + 1])) {
left++;
}
while (left < right && (nums[right] == nums[right - 1])) {
right--;
}
left++;
right--;
} else if ((nums[k] + nums[i] + nums[left] + nums[right]) < target) {
left++;
} else if ((nums[k] + nums[i] + nums[left] + nums[right]) > target) {
right--;
}
}
}
}
return result;
}