一、基本概念
吸引力
F
a
(
n
i
)
=
∑
n
j
∈
N
c
t
d
(
n
i
)
ω
i
,
j
d
E
(
n
i
,
n
j
)
V
i
,
j
\displaystyle \bm{F}_a(n_i)= \sum_{n_j \in \mathcal{N}_{ctd}(n_i)} \omega_{i,j} \; d_E(n_i,n_j) \bm{V}_{i,j}
Fa(ni)=nj∈Nctd(ni)∑ωi,jdE(ni,nj)Vi,j
其中
n
i
n_i
ni代表节点
i
i
i,
N
c
t
d
(
n
i
)
\mathcal{N}_{ctd}(n_i)
Nctd(ni)代表与节点
n
i
n_i
ni相连的所有节点的集合。
ω
i
,
j
\omega_{i,j}
ωi,j是节点
n
i
n_i
ni与节点
n
j
n_j
nj之间边的权重。
d
E
(
n
i
,
n
j
)
d_E(n_i, n_j)
dE(ni,nj)是节点
n
i
n_i
ni与节点
n
j
n_j
nj之间的距离。
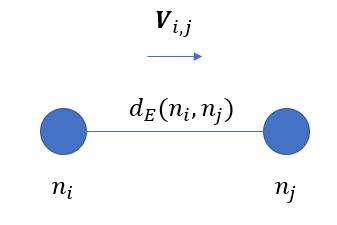
V
i
,
j
\bm{V}_{i,j}
Vi,j是从节点
n
i
n_i
ni倒节点
n
j
n_j
nj之间的单位方向矢量。
| 图1. 吸引力定义中一些基本概念示意图 |
|---|
 |
斥力
F
r
(
n
i
)
=
∑
n
j
∈
N
,
n
≠
n
j
k
r
(
D
(
n
i
)
+
1
)
(
D
(
n
j
)
+
1
)
d
E
(
n
i
,
n
j
)
V
j
,
i
\displaystyle \bm{F}_r(n_i)=\sum_{n_j \in \mathcal{N}, n \neq n_j} k_r \frac{(D(n_i)+1)(D(n_j)+1)}{d_E(n_i,n_j)} \bm{V}_{j,i}
Fr(ni)=nj∈N,n=nj∑krdE(ni,nj)(D(ni)+1)(D(nj)+1)Vj,i
N
\mathcal{N}
N所有节点的集合,
k
r
k_r
kr一个
(
0
,
1
)
(0,1)
(0,1)之间的系数。
D
(
n
i
)
D(n_i)
D(ni)节点
n
i
n_i
ni的度,
D
(
n
j
)
D(n_j)
D(nj)节点
n
j
n_j
nj的度。
V
j
,
i
\bm{V}_{j,i}
Vj,i节点
n
j
n_j
nj倒节点
n
i
n_i
ni的单位方向矢量。
二、关于力引导过程是启发式与否的探讨
问:力引导系统的过程的结果是确定的吗?
答:是
证明过程出发点:
只要证明最终顶点分布是一个确定的结果,是否就证明了该结果是非启发式的。
证明:
力引导过程最终平衡态是指整个系统达到力的平衡
→
\to
→ 所有节点的速度为0,即
v
(
n
i
)
→
0
,
i
=
1
,
⋯
,
N
v(n_i) \to 0,i=1,\cdots,N
v(ni)→0,i=1,⋯,N。下面将开始推导平衡态情况下,节点所处的状态。
按照系统合力为0推导
0
=
F
r
e
s
u
l
t
a
n
t
=
∑
n
i
∈
N
{
F
n
i
节点所受吸引力合力
(
n
i
)
+
F
n
i
节点所受斥力合力
(
n
i
)
}
\bm{0}=\bm{F}_{resultant}=\sum_{n_i \in N} \left\{ \bm{F}_{n_i节点所受吸引力合力}(n_i)+\bm{F}_{n_i节点所受斥力合力}(n_i) \right\}
0=Fresultant=ni∈N∑{Fni节点所受吸引力合力(ni)+Fni节点所受斥力合力(ni)}
=
∑
n
i
∈
N
{
F
a
(
n
i
)
+
F
r
(
n
i
)
}
=\sum_{n_i \in N} \left\{ \bm{F}_a(n_i) + \bm{F}_r(n_i) \right\}
=ni∈N∑{Fa(ni)+Fr(ni)}
=
∑
n
i
∈
N
{
∑
n
j
∈
N
c
t
d
(
n
i
)
ω
i
,
j
d
E
(
n
i
,
n
j
)
V
i
,
j
+
∑
n
k
∈
N
,
n
k
≠
n
i
k
r
(
D
(
n
i
)
+
1
)
(
D
(
n
k
)
+
1
)
d
E
(
n
i
,
n
k
)
V
k
,
i
}
=\sum_{n_i \in N} \left\{ \sum_{n_j \in \mathcal{N}_{ctd}(n_i)} \omega_{i,j} \; d_E(n_i,n_j) \bm{V}_{i,j} + \sum_{n_k \in \mathcal{N}, n_k \neq n_i} k_r \frac{(D(n_i)+1)(D(n_k)+1)}{d_E(n_i,n_k)} \bm{V}_{k,i} \right\}
=ni∈N∑⎩
⎨
⎧nj∈Nctd(ni)∑ωi,jdE(ni,nj)Vi,j+nk∈N,nk=ni∑krdE(ni,nk)(D(ni)+1)(D(nk)+1)Vk,i⎭
⎬
⎫
= ∑ n i ∈ N { 俩节点相同的斥力和吸引力 + 不存在吸引力的节点之间的斥力 } =\sum_{n_i \in N} \left\{ 俩节点相同的斥力和吸引力 + 不存在吸引力的节点之间的斥力 \right\} =ni∈N∑{俩节点相同的斥力和吸引力+不存在吸引力的节点之间的斥力}
= ∑ n i ∈ N { { ∑ n j ∈ N c t d ( n i ) ω i , j d E ( n i , n j ) V i , j + ∑ n j ∈ N c t d ( n i ) k r ( D ( n i ) + 1 ) ( D ( n j ) + 1 ) d E ( n i , n j ) V j , i } + ∑ n k ∈ N , n k ≠ n i k r ( D ( n i ) + 1 ) ( D ( n k ) + 1 ) d E ( n i , n k ) V k , i } =\sum_{n_i \in N} \left\{ \left\{ \sum_{n_j \in \mathcal{N}_{ctd}(n_i)} \omega_{i,j} \; d_E(n_i,n_j) \bm{V}_{i,j} + \sum_{n_j \in \mathcal{N}_{ctd}(n_i)} k_r \frac{(D(n_i)+1)(D(n_j)+1)}{d_E(n_i,n_j)} \bm{V}_{j,i} \right\} + \sum_{n_k \in \mathcal{N}, n_k \neq n_i} k_r \frac{(D(n_i)+1)(D(n_k)+1)}{d_E(n_i,n_k)} \bm{V}_{k,i} \right\} =ni∈N∑⎩ ⎨ ⎧⎩ ⎨ ⎧nj∈Nctd(ni)∑ωi,jdE(ni,nj)Vi,j+nj∈Nctd(ni)∑krdE(ni,nj)(D(ni)+1)(D(nj)+1)Vj,i⎭ ⎬ ⎫+nk∈N,nk=ni∑krdE(ni,nk)(D(ni)+1)(D(nk)+1)Vk,i⎭ ⎬ ⎫
令 d E ( n i , n j ) = d j d_E(n_i,n_j)=d_{j} dE(ni,nj)=dj,其对应的x、y和z三轴分量为 d j x , d j y , d j z d_j^x, d_j^y, d_j^z djx,djy,djz,上述推导过程中存在矢量,下面我将采用解析结合,进一步推导。 V i , j \bm{V}_{i,j} Vi,j在 x x x、 y y y和 z z z轴上的坐标分别为 ( p x , p y , p z ) (p_x, p_y, p_z) (px,py,pz),则 V j , i \bm{V}_{j,i} Vj,i在 x x x、 y y y和 z z z轴上的坐标分别为 ( − p x , − p y , − p z ) (-p_x, -p_y, -p_z) (−px,−py,−pz)。则上述公式可拆分为两个函数 f 1 f_1 f1和 f 2 f_2 f2
f 1 = ( ∑ n j ∈ N c t d ( n i ) { ω i , j d j x p x − k r ( D ( n i ) + 1 ) ( D ( n j ) + 1 ) d j x p x } , ∑ n j ∈ N c t d ( n i ) { ω i , j d j y p y − k r ( D ( n i ) + 1 ) ( D ( n j ) + 1 ) d j y p y } , ∑ n j ∈ N c t d ( n i ) { ω i , j d j z p z − k r ( D ( n i ) + 1 ) ( D ( n j ) + 1 ) d j z p z } ) f_1=\left(\sum_{n_j \in \mathcal{N}_{ctd}(n_i)} \left\{ \omega_{i,j} \; d_j^x p_x - k_r \frac{(D(n_i)+1)(D(n_j)+1)}{d_j^x} p_x \right\}, \sum_{n_j \in \mathcal{N}_{ctd}(n_i)} \left\{ \omega_{i,j} \; d_j^y p_y - k_r \frac{(D(n_i)+1)(D(n_j)+1)}{d_j^y} p_y \right\}, \sum_{n_j \in \mathcal{N}_{ctd}(n_i)} \left\{ \omega_{i,j} \; d_j^z p_z - k_r \frac{(D(n_i)+1)(D(n_j)+1)}{d_j^z} p_z \right\} \right) f1= nj∈Nctd(ni)∑{ωi,jdjxpx−krdjx(D(ni)+1)(D(nj)+1)px},nj∈Nctd(ni)∑{ωi,jdjypy−krdjy(D(ni)+1)(D(nj)+1)py},nj∈Nctd(ni)∑{ωi,jdjzpz−krdjz(D(ni)+1)(D(nj)+1)pz}
f
2
=
∑
n
k
∈
N
,
n
k
≠
n
i
k
r
(
D
(
n
i
)
+
1
)
(
D
(
n
k
)
+
1
)
d
E
(
n
i
,
n
k
)
V
k
,
i
f_2=\sum_{n_k \in \mathcal{N}, n_k \neq n_i} k_r \frac{(D(n_i)+1)(D(n_k)+1)}{d_E(n_i,n_k)} \bm{V}_{k,i}
f2=nk∈N,nk=ni∑krdE(ni,nk)(D(ni)+1)(D(nk)+1)Vk,i
其中,
f
1
f_1
f1是关于各个
d
E
(
n
i
,
n
j
)
d_E(n_i, n_j)
dE(ni,nj)的函数,
f
2
f_2
f2是关于各个
d
E
(
n
i
,
n
k
)
d_E(n_i, n_k)
dE(ni,nk)的函数。再令,
ω
i
,
j
p
x
=
k
1
d
j
x
\omega_{i,j} p_x=k_1^{d_j^x}
ωi,jpx=k1djx和
−
k
r
(
D
(
n
i
)
+
1
)
(
D
(
n
j
)
+
1
)
p
x
=
k
2
d
j
x
-k_r (D(n_i)+1)(D(n_j)+1) p_x=k_2^{d_j^x}
−kr(D(ni)+1)(D(nj)+1)px=k2djx、
ω
i
,
j
p
y
=
k
1
d
j
y
\omega_{i,j} p_y=k_1^{d_j^y}
ωi,jpy=k1djy和
−
k
r
(
D
(
n
i
)
+
1
)
(
D
(
n
j
)
+
1
)
p
y
=
k
2
d
j
y
-k_r (D(n_i)+1)(D(n_j)+1) p_y=k_2^{d_j^y}
−kr(D(ni)+1)(D(nj)+1)py=k2djy、
ω
i
,
j
p
z
=
k
1
d
j
z
\omega_{i,j} p_z=k_1^{d_j^z}
ωi,jpz=k1djz和
−
k
r
(
D
(
n
i
)
+
1
)
(
D
(
n
j
)
+
1
)
p
z
=
k
2
d
j
z
-k_r (D(n_i)+1)(D(n_j)+1) p_z=k_2^{d_j^z}
−kr(D(ni)+1)(D(nj)+1)pz=k2djz。那么函数
f
1
f_1
f1则为
f 1 = ( ∑ n j ∈ N c t d ( n i ) { k 1 d j x d j x + k 2 x j d j x } , { k 1 d j y d j y + k 2 d j y ) d j y } , { k 1 d j z d j z + k 2 d j z ) d j z } ) f_1=\left(\sum_{n_j \in \mathcal{N}_{ctd}(n_i)} \left\{ k_1^{d_j^x} d_j^x + \frac{k_2^{x_j}}{d_j^x} \right\}, \left\{ k_1^{d_j^y} d_j^y + \frac{k_2^{d_j^y})}{d_j^y} \right\}, \left\{ k_1^{d_j^z} d_j^z + \frac{k_2^{d_j^z})}{d_j^z} \right\} \right) f1= nj∈Nctd(ni)∑{k1djxdjx+djxk2xj},{k1djydjy+djyk2djy)},{k1djzdjz+djzk2djz)}
此时求偏导
{
∂
f
1
∂
x
=
0
∂
f
1
∂
y
=
0
∂
f
1
∂
z
=
0
\left\{\begin{array}{l} \frac{\partial f_1}{ \partial x}=0 \\ \frac{\partial f_1}{ \partial y}=0 \\ \frac{\partial f_1}{\partial z}=0 \end{array} \right.
⎩
⎨
⎧∂x∂f1=0∂y∂f1=0∂z∂f1=0
由于距离只能为正,为了使得函数
f
1
f_1
f1最小,应满足距离满足如下情况
(1)根据函数
f
1
f_1
f1,相互连接的节点之间应满足距离
k
1
d
j
k
2
d
j
\frac{k_1^{d_j}}{k_2^{d_j}}
k2djk1dj;
(2)根据函数
f
2
f_2
f2,没有连接的节点之间的距离趋于无穷大。
![[蓝桥杯]真题讲解:数三角(枚举+STL)](https://img-blog.csdnimg.cn/direct/27129fb34d6a405bbb527ec6d2253fa9.png)