根结点：非空树中无前驱节点的结点
结点度：结点拥有的子树数或子节点数或后继节点数
树的度：树内各结点的度的最大值
叶子：终端节点，度为0
祖先：从根到该节点所经分支上的所有结点
子孙：以某结点为跟的子树中的任意节点

深度 （从上往下数）
树的深度：距离根结点最远的结点所处的最大层数即为树的深度。

下图中
树深度为5
A结点的深度为1（处在第1层）
G结点的深度为3（处在第3层）

高度（从下往上数）
树的高度：树的高度和树的深度相同，叶结点的高度为1，非叶结点的高度等于它的子女结点高度的最大值+1

G的高度为3、M高度为2，O的高度1
F的高度为1

注：节点的高度和深度是不同的。

总结：1.所有节点中，节点最大的度，即为树的度
           2.所有节点的深度/高度的最大值即为树的深度和高度
           

树的路径长度：指从根节点到每个节点的路径之和,或者是所有路径的长度的总和
节点路径长度：节点与节点之间的路径长度
所有节点的路径长度之和为树的路径长度

图中树的度为3：
树的所有结点=所有结点的度+1。
 区别一下2种情况
 总结点=所有结点的度之和+1
 总结点=所有度的节点数量之和。  度为0的结点+度为1的结点+度为2的节点+度为.n的结点
 

叶子节点=所有节点-非零度的节点个数。

二叉树性质
1.深度为K的二叉树至多有2的k次方-1个节点k>=1  ，至多实际指满二叉树的情况
深度为k时至少有k个结点。

2.在二叉树的第i层上至多有2的i-1次方个节点（i>=1）

一、二叉树性质：任何一个二叉树，如果叶子数为n。，度为2的节点数为n2，则n。= n2+1；

---

二、哈弗曼树概率
路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。
结点的路径长度：两结点间路径上的分支数。 
树的路径长度：从树根到每一个结点的路径长度之和
权：给树中结点赋一个有某种含义的数值，则这个数值称为该结点的权。
结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度WPL：树中所有叶子结点的带权路径长度之和 
哈弗曼树：最优树 ，带权路径长度（WPL）最短的树。
带权路径长度最短，是在度相同的树中比较而得出的结果，因此有最优二叉树，最优三叉树之称

满二叉树不一定是哈弗曼树
哈夫曼树中权越大的叶子离根越近
具有相同带权结点的哈弗曼树不唯一

三、哈弗曼树的构造算法
1.构造森林全是根
2.选用两小造新树
3.删除两小添新人
4.重复2、3

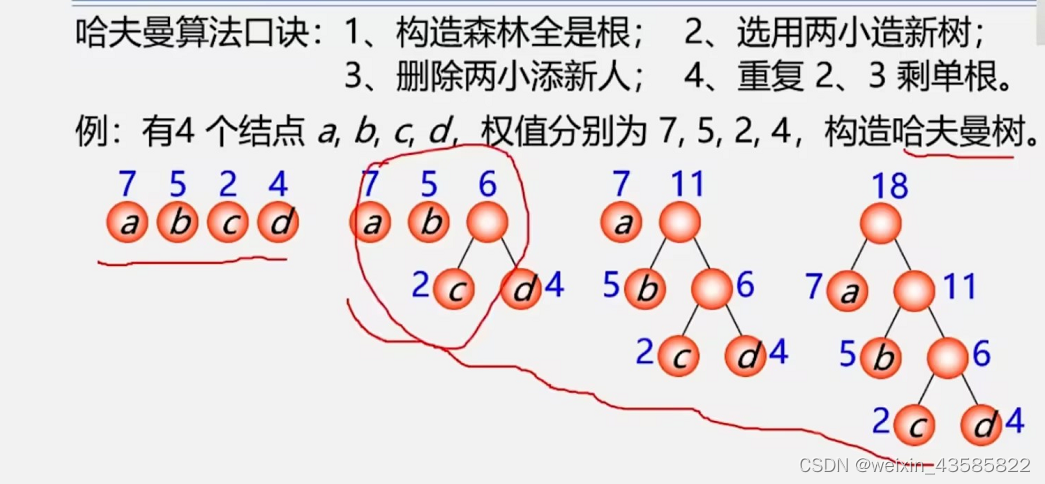
哈夫曼树的结点的度数为0或2，没有度为1的结点。

包含n个叶子结点的哈夫曼树中共有2n-1个结点

哈弗曼树总结：
1.在哈夫曼算法中，初始化时有n棵二叉树，要经过n-1次合并最终形成哈弗曼树。
2.经过n-1次合并产生n-1个新结点，且这n-1个新结点都是具有两个孩子的分支结点。

四、哈夫曼树的构造算法实现

采用顺序存储结构------一维结构数组
结点类型定义